Lunar Landing NRN Sim

It first creates an optimal 2D trajectory which is transformed into 3D for a north pole landing. It replicates the trajectory in a simulation. There are 3 sections:

1. Compute optimal trajectory 2. Run a simulation with the computed acceleration 3. Test optical navigation

You can run each independently once all three sections have run.

The simulation results are used in the Kalman Filter for testing.

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2021 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2021.1
%--------------------------------------------------------------------------

Compute the optimal landing trajectory

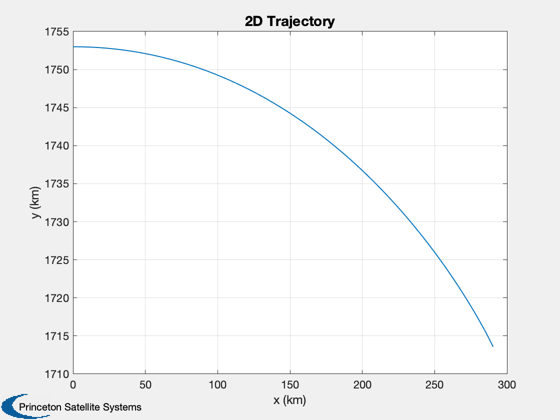
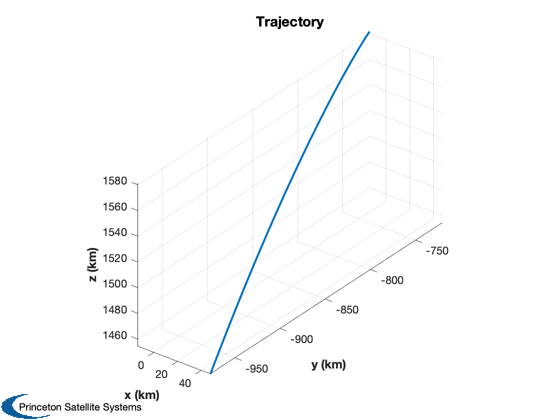
It optimizes a 2D trajectory then transforms it into a 3D trajectory in ECI

% Constants
rM        = Constant('equatorial radius moon');
mu        = Constant('mu moon');
secInDay  = 86400;
mInKm     = 1000;

% Start at 15 km
r   = rM + 15;
d   = LunarTrajectoryControl;
x   = [r;0;0;0;0;sqrt(mu/r)]; % Circular polar orbit Lunar fixed
x   = LFToECI(x,d.jDTarget) % Convert to ECI
p   = Period(r,mu);
jD  = d.jDTarget - (p/4)/secInDay;

% It will print out the optimization steps
d   = LunarTrajectoryControl( 'initialize', x, jD, d );

% Plot
Plot2D( d.xP2D(1,:), d.xP2D(2,:),'x (km)','y (km)','2D Trajectory');
Plot3D( d.xTrajECI(1:3,:), 'x (km)', 'y (km)', 'z (km)', 'Trajectory'  );

% Plot the orbit around the moon
PlotPlanetaryOrbit( d.xTrajECI(1:3,:), 'Moon', d.tTraj, d.jDStart );

x =
      -369.01
         1589
       641.85
     -0.02784
     -0.63248
       1.5498
                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0     201    3.434516e+02    5.617e+01    8.798e-03
    1     402    3.317403e+02    3.325e+00    1.276e+00    4.184e+00
    2     603    3.598487e+02    1.126e+00    7.909e-01    2.862e+00
    3     804    3.599938e+02    1.558e-02    2.652e-01    3.585e-01
    4    1005    3.602424e+02    5.385e-04    1.000e-01    8.872e-02
    5    1206    3.602436e+02    2.993e-04    2.167e-02    5.793e-02
    6    1407    3.602499e+02    2.625e-05    1.052e-02    1.325e-02
    7    1608    3.602499e+02    1.971e-06    4.712e-03    9.874e-03

Optimization completed: The relative first-order optimality measure, 4.711497e-03,
is less than options.OptimalityTolerance = 1.000000e-02, and the relative maximum constraint
violation, 3.509356e-08, is less than options.ConstraintTolerance = 1.000000e-02.

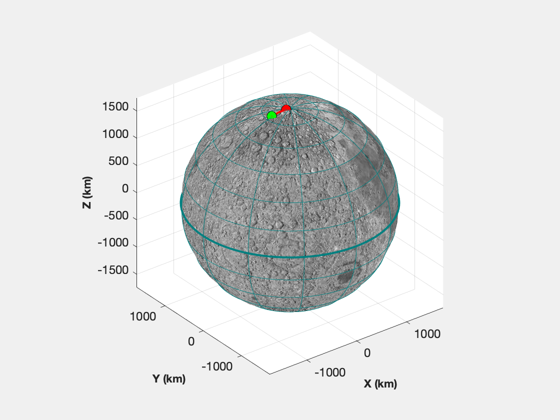
Run a simulation with the computed acceleration

% These states are used as the measurement input for the next section
n 	= length(d.tTraj);

% Pre-allocate memory
xPS = zeros(6,n);

% Initial state from the optimal trajectory
x   = d.xTrajECI(:,1);
dT	= d.tTraj(2);

% Get the data structure
dRHS = RHSPlanet3DONS;

% Run the simulation
for k = 1:n
	xPS(:,k)	= x;
  dRHS.acc  = d.a(:,k);
  x         = RK4(@RHSPlanet3DONS,x,dT,0, dRHS);
end

% Plotting
yS      = {'x (km)' 'y (km)' 'z (km)' 'h (km)'};
[t,tL]  = TimeLabl(d.tTraj);

h       = Mag(xPS(1:3,:)) - rM;
Plot2D(t,[xPS(1:3,:);h],tL,yS,'Simulated Trajectory');

h       = Mag(d.xTrajECI(1:3,:)) - rM;
Plot2D(t,[d.xTrajECI(1:3,:);h],tL,yS,'Optimal Trajectory');

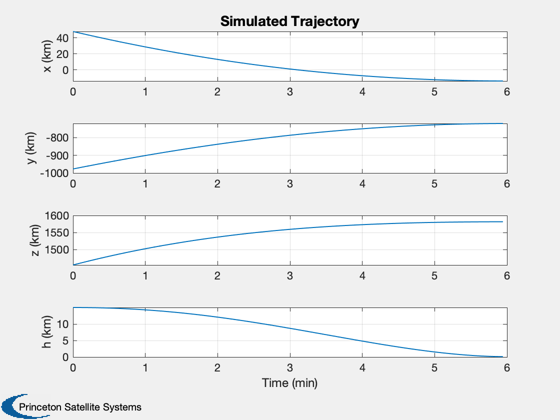
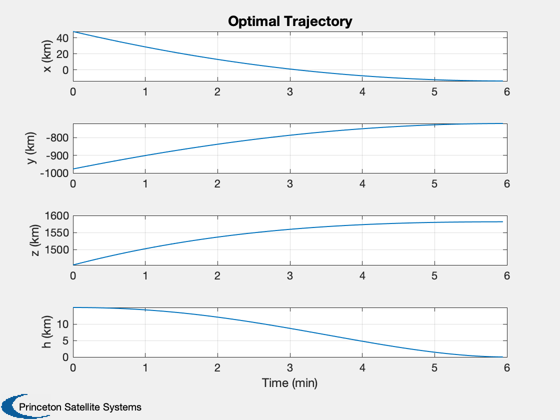
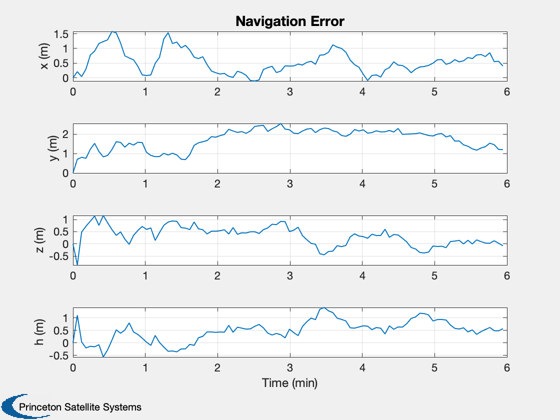
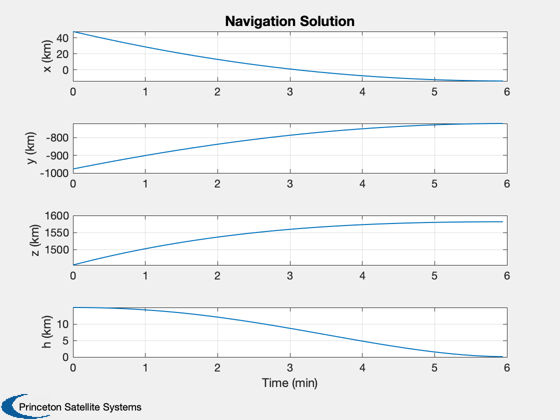
Test optical navigation

% Set up optical navigation
dONS                = OpticalNavigation;
dONS.target         = 1; % The moon
dONS.useUKF         = true;
dONS.ukf.useState   = false;
dONS.ukf.usePos     = true;
dONS.ukf.useOptical	= false;
dONS.ukf.f          = @RHSPlanet3DONS;
dONS.ukf.fData      = RHSPlanet3DONS;
dONS.t              = 0;
dONS.ukf.x          = d.xTrajECI(:,1);
dONS.ukf.m          = d.xTrajECI(:,1);

% Measurement noise
oneSigma            = [0.01;0.01;0.01;0;0;0]; % 10 m from the neural network

% Initialize
dONS  = OpticalNavigation( 'initialize', dONS,  d.xTrajECI(1:3,1), d.xTrajECI(4:6,1), dT );

% Pre-allocate memory
xP    = zeros(6,n);

% Run the estimator
for k = 1:n
	xP(:,k)     = dONS.x;
	meas.state	= xPS(:,k) + oneSigma.*randn(6,1);
  meas.acc    = d.a(:,k);
  dONS.t      = d.tTraj(k);
  dONS        = OpticalNavigation( 'update trn', dONS, meas );
end

% Plot
[t,tL]	= TimeLabl(d.tTraj);

% Altitude above a spherical moon
h       = Mag(xPS(1:3,:)) - rM;
hS      = Mag(xP(1:3,:))  - rM;

ySM      = {'x (m)' 'y (m)' 'z (m)' 'h (m)'};

Plot2D(t,[xP(1:3,:) - xPS(1:3,:);h-hS]*mInKm,tL,ySM,'Navigation Error');
Plot2D(t,[xP(1:3,:);hS],tL,yS,'Navigation Solution');

% Makes a GUI with all plots
Figui


%--------------------------------------

Published with MATLAB® R2021a