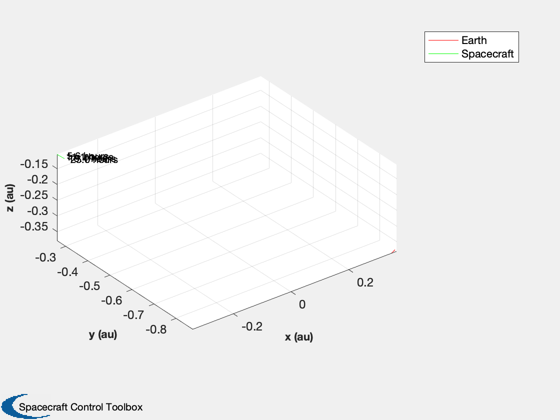
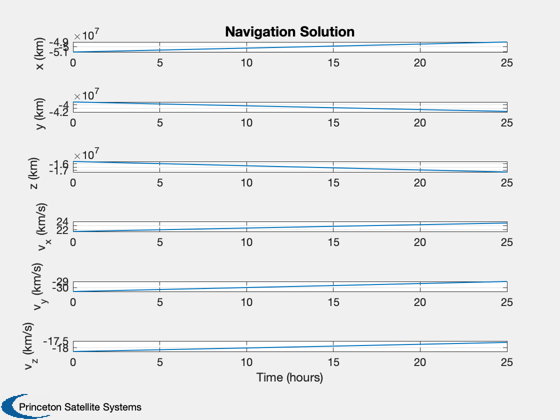
Simulate ONS for a spacecraft that flies by Mercury
This only simulates the orbital motion.
See also: RHSHelioMission, PlanetPosJPL, NavigationCamera, StarCameraViewer, RHSUKFHelioMission, MeasGPS, MeasRangeGroundStation, MeasStarAngleAndChord, OpticalNavigation, RK4, TimeLabl, Plot2D, Figui
Contents
%-------------------------------------------------------------------------- % Copyright (c) 2021 Princeton Satellite Systems, Inc. % All rights reserved. %--------------------------------------------------------------------------
Constants
rE = Constant('equatorial radius mercury'); rS = Constant('sun radius'); muSun = Constant('mu sun'); muMercury = Constant('mu mercury'); aU = Constant('au'); secToDay = 1/86400; secInYear = 365.26*86400; kEarth = 1; % SPICE numbering 1-9 are the planets, 10 is the moon mercury = 1; sun = 2; % Get the defaults dRHS = RHSHelioMission; dRHS.mu(1) = muMercury;
Script control
viewersOn = true; printAll = false; % acceleration model massFuel = 0; % kg dRHS.mD = 1000; % kg dRHS.uE = inf; plotRef = {'Sun' 'Mercury'}; % Initialize the ephemeris PlanetPosJPL( 'initialize', kEarth ) rHelio = [-5.102050761318097E+07; -3.914630171469574E+07; -1.563888544075625E+07]; vHelio = [ 2.159852087150890E+01; -3.063444535492430E+01; -1.827429443660471E+01]; jD0 = 2455755.50; % Initialize the state dRHS.ref = sun; dT = 10000; tEnd = 10*dT; % sec % This halo state does not take into account the sail's force [r0, mu, v0] = PlanetPosJPL( 'update', jD0 ); x = [rHelio;vHelio;massFuel]; dRHS.mu(1) = mu; % set the mu for the right planet % Set the Julian date for the dynamical model dRHS.jD0 = jD0; % Simulation steps n = ceil(tEnd/dT);
Setup the camera data structure
dCam = NavigationCamera; dGPS = MeasGPS; dGS = MeasRangeGroundStation; dOM = MeasStarAngleAndChord;
Add noise
dCam.camera.sigmaXY = 1;
dCam.camera.noise = true;
dCam.namePlanet = {'Mercury' 'Sun'};
dCam.radiusPlanet = [rE rS];
Set up the displays
TimeDisplay('initialize','ONS Simulation',n); if( viewersOn ) hNav = StarCameraViewer('initialize','Navigation Camera', n ); %#ok<*UNRCH> end % The time vector t = (0:n-1)*dT;


Setup Optical Navigation
dONS = OpticalNavigation; r = x(1:3); v = x(4:6); dONS.ukf.fData = RHSUKFHelioMission; dONS.ukf.fData.mu(1) = muMercury; dONS.ukf.fData.jD0 = dRHS.jD0; dONS.target = mercury; dONS.ukf.fData.ref = sun; % Initialize ONS dONS = OpticalNavigation( 'initialize', dONS, r, v, dT ); meas.optical = NavigationCamera( r, dCam ); % Set up the parameters in ONS dONS.t = t(1); dONS.useUKF = true; dONS.ukf.useOptical = false; dONS.ukf.useState = false; dONS.ukf.usePos = false; dONS.ukf.f = @RHSUKFHelioMission; dONS.aBody1 = rE; dONS.aBody2 = rS; dONS.ref = dRHS.ref; % Plotting arrays xP = zeros(20,n); target = zeros(1,n); type = zeros(1,n); nStars = zeros(1,n);
Run the simulation
for k = 1:n % ONS simulation TimeDisplay('update',k); % Get data for plotting [~,~,~,acc] = RHSHelioMission(x,t(k),dRHS); % Get the location and velocity of Earth [rMercury,~,vMercury] = PlanetPosJPL( 'update', jD0 + t(k)*secToDay ); if( dRHS.ref == mercury ) dCam.xPlanet = [[0;0;0] -rMercury]; rMercury = [0;0;0]; vMercury = [0;0;0]; else dCam.xPlanet = [rMercury [0;0;0]]; end % The camera boresight points at the target xCam is in the helio frame rCam = x(1:3); vCam = x(4:6); % Needed to point the camera dONS = OpticalNavigation( 'get unit vector', dONS, rMercury, vMercury, rCam, vCam ); % Get the measurements meas.jD0 = jD0 + t(k)*secToDay; meas.state = x(1:6); meas.acc = acc; dCam.q = U2Q(dONS.uC,[0;0;1]); dOM.cam = NavigationCamera( rCam, dCam ); dOM.type = dONS.type; dOM.target = dONS.target; dOM.ref = dRHS.ref; dOM.uCamera = dONS.uCamera; dOM.aBody1 = dONS.aBody1; dOM.aBody2 = dONS.aBody2; dOM.r1 = rMercury; dOM.v1 = vMercury; % Measurements meas.state = x(1:6); meas.acc = acc; % Spacecraft non-gravitational acceleration meas.gps = MeasGPS( x, dGPS ); meas.gs = MeasRangeGroundStation( x, dGS ); meas.optical = MeasStarAngleAndChord( [rCam;vCam], dOM ); % ONS dONS.cam = dOM.cam; dONS.ref = dRHS.ref; dONS.r1 = dOM.r1; dONS.v1 = dOM.v1; dONS.t = t(k); dONS = OpticalNavigation( 'update', dONS, meas, rMercury, vMercury, rCam, vCam ); target(k) = dONS.target; type(k) = dONS.type; nStars(k) = dONS.ukf.optical.nStars; % Display the cameras if( viewersOn ) StarCameraViewer('update', dOM.cam, [], hNav, dCam, k); end xP(:,k) = [x;rMercury;dRHS.thrust;dRHS.ref;dONS.x]; % Propagate the state x = RK4(@RHSHelioMission,x,dT,t(k),dRHS); end TimeDisplay('close');
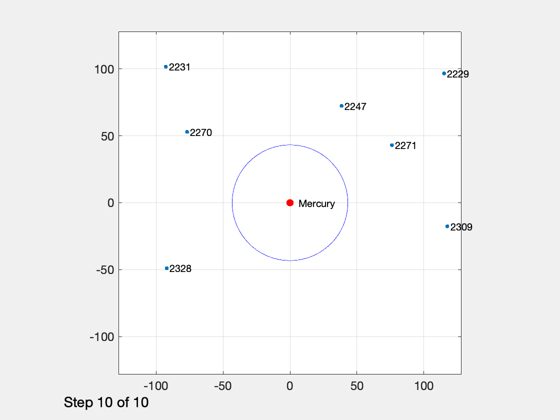
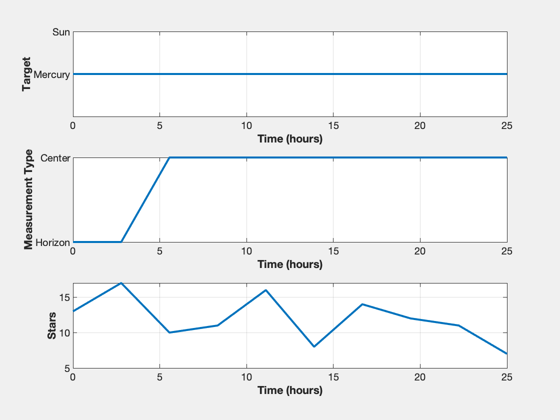
Plotting
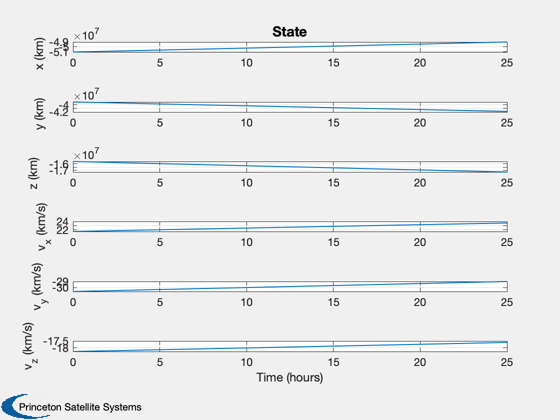
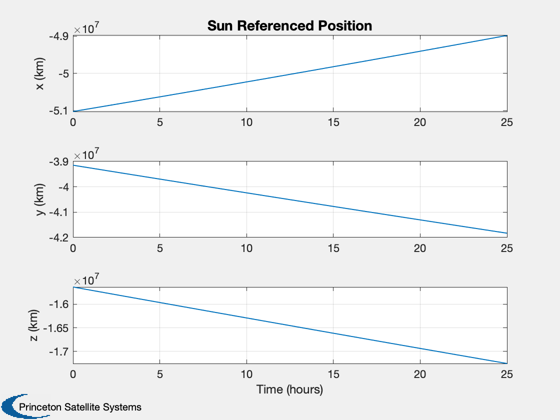
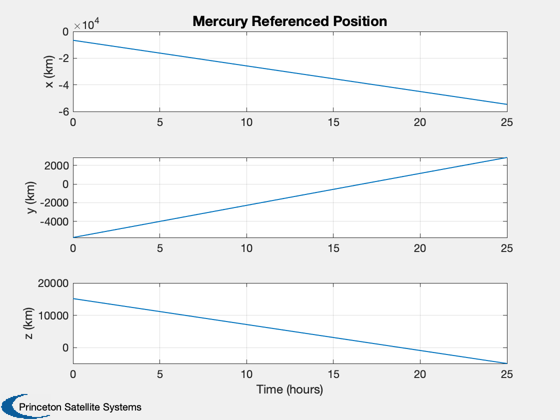
% Shorten the vectors if it hits the ground j = 1:k; xP = xP(:,j); t = t(j); target = target(j); type = type(j); nStars = nStars(j); % Make earth and sun referenced positions rSun = zeros(3,k); rMercury = zeros(3,k); j = find(xP(14,:) == mercury ); rMercury(:,j) = xP(1:3,j); rSun(:,j) = xP(8:10,j) - rMercury(:,j); j = find(xP(14,:) == sun ); rSun(:,j) = xP(1:3,j); rMercury(:,j) = xP(8:10,j) - rSun(:,j); % Sun/Mercury plot HelioPlot( 3, t(end)/secInYear, jD0, xP(1:3,:), {'Spacecraft'} ) % Time histories [t,tL] = TimeLabl(t); yL = {'x (km)' 'y (km)' 'z (km)'}; yS = {'x (km)' 'y (km)' 'z (km)' 'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)'}; Plot2D(t,xP(1:6,:),tL,yS,'State'); Plot2D(t,rSun, tL,yL,'Sun Referenced Position'); Plot2D(t,rMercury,tL,yL,'Mercury Referenced Position'); Plot2D(t,xP(15:20,:) - xP(1:6,:),tL,yS,'Navigation Error'); Plot2D(t,xP(15:20,:),tL,yS,'Navigation Solution'); NewFig('Targeting') subplot(3,1,1); h = plot(t,target); set(h,'linewidth',2); grid on XLabelS(tL); YLabelS('Target') set(gca,'ytick',[1 2],'yticklabel',{'Mercury' 'Sun'}); subplot(3,1,2); h = plot(t,type); set(h,'linewidth',2); grid on XLabelS(tL); YLabelS('Measurement Type') set(gca,'ytick',[1 2],'yticklabel',{'Horizon' 'Center'}); subplot(3,1,3); h = plot(t,nStars); set(h,'linewidth',2); grid on XLabelS(tL); YLabelS('Stars') Figui if( printAll ) n = get(gcf,'number'); for k = 1:n PrintFig(1,4,k,sprintf('%s%d',simName,k)); end end %--------------------------------------