Contents

SyntheticTerrain is a script created to create synthetic terrain

Allan et al.'s work https://doi.org/10.1109/AERO.2019.8741780 to create a s terrain generator for the lunar surface to create high resolution images from the currently available low resolution images from http://imbrium.mit.edu/

This script upscales the input image and outputs a synthetic higher resolution version of the input image:

1. separates the high and low frequencies of the input image 2. performs fractal synthesis by the diamond-square method on the high frequency portion of the image and uses the Catmull-Rom spline interpolation method to generate new data 3. performs bilinear interpolation on the low frequency component of the image 4. recombines the high and low frequencies of the input image and returns the final image

key input variables the user can change:

c_img - the input image (this should be a dem but the script was mostly tested on optical images. may need different frequency splitting method for low contrast dems avaialable.) the input image needs to be a square with even # of pixels. I recommend starting with a small 500x500 image.

scale - determines the upscaling of the input image. this needs to be a power of 2. i.e. scale = 2, 4, 8, 16 etc.

freq - determines the frequency split between high and low frequencies. make use of the figure showing the frequency split to determine what the frequency should be for the input image. This needs to be between [0,1].

interp - sets the interpolation method. by default this is 'spline' for Catmull-Rom Spline and 'linear', or linear interpolation, is only used on edge cases. However this can be changed to 'linear' for the entire image for comparison. This can only be 'spline' or 'linear'.

key outputs:

hmap - final heightmap. this is the upscaled input image. size will be scale*input image size

method - matrix with indices indicating if a pixel was interpolated with the square or diamond method and the iteration number. 1:iter_max are squares for each iteration. iter_max+1:iter_max+iter_max are diamonds for each iteration. useful for debugging or for understanding final image artifacts.

Online resources:

Diamond-square method https://stevelosh.com/blog/2016/06/diamond-square/

catmull rom spline https://en.wikipedia.org/wiki/Centripetal_Catmull%E2%80%93Rom_spline

%--------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2021 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2021.1
%--------------------------------------------------------------------------

% Lunar image
file  = 'LunarSurfaceImage.png';
dem   = imread(file);
demt  = dem/max(dem(:));
c_img	= demt(1:512,1:512);

Fourier transform to separate high and low freq data

Taken from Maggie Kautz's homework for OPTI 512L from UArizona fourier transforms to split high and low frequencies by freq input variable

% Fourier transform original image
F = fftshift(fft2(fftshift(c_img)));

% Make a meshgrid the same size as input image
xi = linspace(-1,1,length(c_img));
eta = xi;
[XI, ETA] = meshgrid(xi,eta);

% Change this variable to change frequency split
freq = 0.01; % bounds [0,1]

% Use meshgrid to greate high and low pass filters
LPF = (abs(XI) < freq) & (abs(ETA) < freq); %low pass filter only lets in xi < abs(freq) frequencies
HPF = 1 - LPF; % high pass filter blocks xi < abs(freq) frequencies

% Use high and low pass filters on fourier transform of the original image
Img_LPF = F.*LPF;
Img_HPF = F.*HPF;

% Inverse fourier transform to return data we can use
img_lpf = fftshift(ifft2(fftshift(Img_LPF)));
img_hpf = fftshift(ifft2(fftshift(Img_HPF)));

% Take real portion of inverse fft for visualization purposes
lpf_data = real(img_lpf);
hpf_data = real(img_hpf);

% Make real portion of fft into rgb images for visualizations at the end of
% the code
lpf_img = imRGB(lpf_data,255);
hpf_img = imRGB(hpf_data,1);

% Plot frequency split to see if freq variable needs to be changed
NewFig('Frequency Split');
subplot(1,2,1)
imagesc(xi,eta, lpf_data)
colormap(gray)
axis square
title('Low Pass Filter')

subplot(1,2,2)
imagesc(xi,eta, hpf_data)
colormap(gray)
axis square
title('High Pass Filter')

sgtitle(sprintf('Frequency %0.2f',freq))

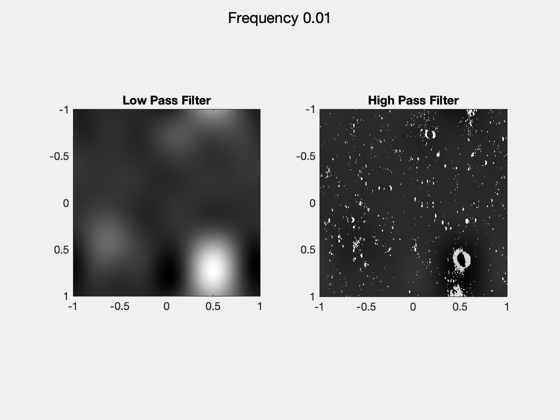
High freq: square-diamond interpolation

% perform square-diamond interpolation only on high frequency portion
image = hpf_data;

% get size of high frequency portion
[m,n] = size(image);

% set upscaling factor (needs to be power of 2: 2,4,8,16, etc.)
scale = 2;

% set interpolation method (either 'linear' or 'spline')
interp = 'spline';

% initilize heightmap and diamond-square method output
hmap = zeros(m*scale,n*scale);
method = zeros(m*scale,n*scale);

% add existing data to heightmap
original_x = zeros(m*n,1);
original_y = zeros(m*n,1);
count = 1;
for i = 1:m
    for j = 1:n
        % position original data determined by scale*x+1,scale*y+1
        % starts at 1,1 when x=y=0
        hmap(scale*(i-1)+1,scale*(j-1)+1) = image(i,j);

        % save position of original data
        original_x(count) = scale*(i-1)+1;
        original_y(count) = scale*(j-1)+1;

        count = count + 1;
    end
end

% rename original data to square input variables
s_in_x = original_x;
s_in_y = original_y;

iteration = 1; % increases for each iteration of square+diamond
iter_max = log(scale)/log(2); % max # of iteration determined by scale
for i = 1:iter_max

[hmap, so_x, so_y, method] = square(hmap, interp, iteration, scale, m, n, s_in_x, s_in_y, method);
[hmap, s_in_x, s_in_y, method] = diamond(hmap, interp, iteration, scale, m, n, so_x, so_y, method);

iteration = iteration + 1;
end

Low freq: bilinear interpolation

% use matlab function to bilinear interpolate low frequency data
bi = imresize(lpf_data,scale,'bilinear');

Rejoin frequencies

recombine processed high and low frequencies

combo = hmap + bi;

% normalize
combo = combo/max(combo,[],'all');

% make rgb for visualization
combo_rgb = imRGB(combo,1);

Plotting

% Original terrain image
NewFig('Original Image');
imshow(c_img)
title('Original Lunar Terrain Image')

% subplots to see before and after for low and high frequencies
NewFig('Low Frequency');
subplot(1,2,1)
imshow(lpf_img)
title('Original Low Frequency')
subplot(1,2,2)
imshow(imRGB(bi,1))
title('Low Frequency Bilinear Interpolation')

NewFig('High Frequency');
subplot(1,2,1)
imshow(hpf_img)
title('Original High Frequency')
subplot(1,2,2)
imshow(imRGB(hmap,1))
title('High Frequency Catmull Rom Spline Interpolation')

% final output image
NewFig('Combined');
imshow(combo_rgb)
title(sprintf('Combined Low and High Frequency Simulated High Resolution Image. Scale %d Split Frequency %0.2f',scale, freq))

Figui

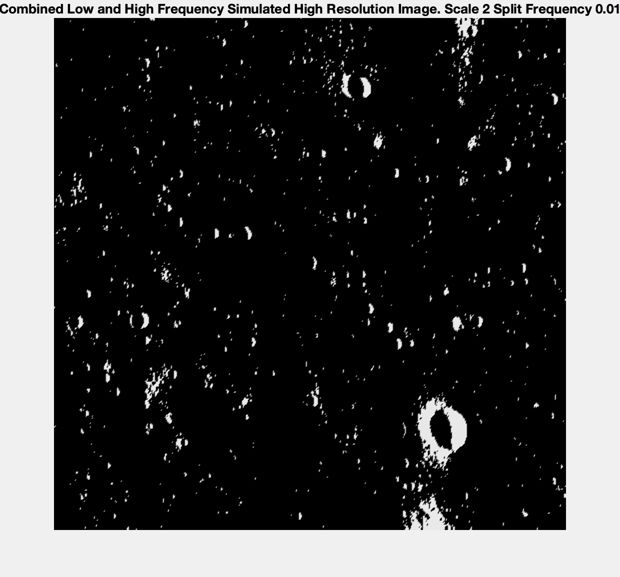
Square interpoloation

function [hmap, output_locations_x, output_locations_y, method] = square(hmap, interp, iteration, scale, im_m, im_n, input_location_x, input_location_y, method)
% function to perform square portion of square-diamond interpolation

fprintf('Performing square iteration %d out of %d\n',iteration,log(scale)/log(2))

% get size of input data
m = length(input_location_x);
n = length(input_location_y);

% initilize arrays to store square locations
square_locations_x = zeros(m,1);
square_locations_y = zeros(n,1);

count = 1;
for i=1:m % for size of input data

    % input data locations
    x = input_location_x(i);
    y = input_location_y(i);

    % if x or y are zero, print and break
    if (x == 0) | (y == 0)
        fprintf('Input data is zero. Miscalculated # of outputs of previous function\n breaking at %d of %d\n', i, m)
        break
    end

    % for each input pixel, find distance to next input pixel in x & y
    distance = scale/(2^(iteration-1));
    x_add = distance;
    y_add = distance;

    interp_2 = interp; % for all data use original interpolation method

    % check if pixel is on edge of image
    x_edge = (x+x_add)>=scale*im_m;
    y_edge = (y+y_add)>=scale*im_n;

    input_data=[]; % initialize input data
    % if input pixel on edge, only take existing data and do linear instead of spline
    % use linear on edge cases bc spline needs 4 data points
    if x_edge & ~y_edge
        input_data = [hmap(x,y),hmap(x,y+y_add)];
        interp_2 = 'linear';
    elseif y_edge & ~x_edge
        input_data = [hmap(x,y),hmap(x+x_add,y)];
        interp_2 = 'linear';
    elseif x_edge & y_edge
        input_data = [hmap(x,y)];
        interp_2 = 'linear';
    else
        % if input pixel not on edge, take surrounding four corner pixels
        try
            input_data = [hmap(x,y),hmap(x,y+y_add),hmap(x+x_add,y),hmap(x+x_add,y+y_add)];
        catch
            fprintf('caught error. usually is an out of bounds error. check input_data')
        end
    end

    % use distance to find placement of new square pixel
    sx = x + distance/2;
    sy = y + distance/2;

    % store square pixel locations
    square_locations_x(count) = sx;
    square_locations_y(count) = sy;

    % depending on if pixel is on edge or not, use linear or spline to
    % interpolate new square pixel value and store in hmap
    switch interp_2
        case 'spline'
            % take spline average
            hmap(sx,sy) = CatmullRomSpline(input_data(:));
        case 'linear'
            % take linear average
            hmap(sx,sy) = mean(input_data,'all');

    end
    count = count + 1;

    % store square method
    method(sx,sy) = iteration;

end

% combine input locations and square locations to pass to diamond function
output_locations_x = [input_location_x; square_locations_x];
output_locations_y = [input_location_y; square_locations_y];
end

Performing square iteration 1 out of 1

Diamond interpolation

function [hmap, output_locations_x, output_locations_y, method] = diamond(hmap, interp, iteration, scale, im_m, im_n, input_location_x, input_location_y, method);
% function to perform diamond portion of square-diamond interpolation

fprintf('Performing diamond iteration %d out of %d\n',iteration,log(scale)/log(2))

% get size of input data
m = length(input_location_x);
n = length(input_location_y);

% initilize arrays to store square locations
diamond_locations_x = zeros(2*m - im_m*iteration - im_n*iteration,1);
diamond_locations_y = zeros(2*n - im_m*iteration - im_n*iteration,1);

count = 1;
for i=1:m % for size of input data

    % input data locations
    x = input_location_x(i);
    y = input_location_y(i);

    % if x or y are zero, print and break
    if (x == 0) || (y == 0)
        fprintf('input data is zero. miscalculated # of outputs of previous function\n breaking at %d of %d\n', i, m)
        break
    end

    % distance to next input pixel in x & y
    distance = scale/(2^(iteration-1));

    % if input location is on the bottom or right edge, don't create a new
    % diamond past the edge of the frame
    start = 1;
    stop = 2;
    if (x + distance/2) >= scale*im_m
        % only create second diamond
        start = 2;
        stop = 2;
    end
    if (y + distance/2) >= scale*im_n
        % only create first diamond
        start = 1;
        stop = 1;
    end
    if ((x + distance/2) >= scale*im_m) & ((y + distance/2) >= scale*im_n)
        % create no diamonds and continue to next input location
        fprintf('Found corner. Continue happening at i = %d out of %d.\n',i,m)
        continue
    end

    % create two diamonds for each input location
    for k=start:stop
        if k == 1
            % first diamond location
            xd = x + distance/2;
            yd = y;
        end
        if k == 2
            % second diamond location
            xd = x;
            yd = y + distance/2;
        end

        % store new diamond location for output later
        diamond_locations_x(count) = xd;
        diamond_locations_y(count) = yd;

        % this is the x,y to add to diamond location to find our data to
        % average
        x_add = distance/2;
        y_add = distance/2;

        interp_2 = interp; % for all data use original interpolation method

        data = []; % initialize data variable
        % find four surrounding pixels for diamond average calculation
        % make sure the x,y we are adding is not past the image frame
        x_edge = (xd + x_add) > scale*im_m;
        y_edge = (yd + y_add) > scale*im_n;

        % edge effects for x
        if xd == 1
            % take only pixel below
            down = hmap(xd + x_add,yd);
            data = [data, down];
            interp_2 = 'linear';
        end
        if x_edge
            % take only pixel above
            up = hmap(xd - x_add,yd);
            data = [data, up];
            interp_2 = 'linear';
        end
        if ~x_edge & xd~=1 % if not on edge
            % take both pixels above and below
            up = hmap(xd - x_add,yd);
            down = hmap(xd + x_add,yd);
            data = [data, up, down];
        end

        %edge effects for y
        if yd == 1
            % take only pixel to the right
            right = hmap(xd,yd + y_add);
            data = [data, right];
            interp_2 = 'linear';
        end
        if y_edge
            % take only pixel to the left
            left = hmap(xd,yd - y_add);
            data = [data, left];
            interp_2 = 'linear';
        end
        if yd~=1 && ~y_edge % if not on edge
            % take both pixels to the right and left
            left = hmap(xd,yd - y_add);
            right = hmap(xd,yd + y_add);
            data = [data, left, right];
        end

        % depending on if pixel is on edge or not, use linear or spline to
        % interpolate new square pixel value and store in hmap
        switch interp_2
            case 'linear' % linear interpolation
                hmap(xd,yd) = mean(data,'all');
            case 'spline' % Catmull Rom spline
                hmap(xd,yd) = CatmullRomSpline(data);
        end
        count = count + 1;

        % store diamond method
        method(xd,yd) = iteration + log(scale)/log(2);
    end
end

% combine input locations and square locations to pass to square function
output_locations_x = [input_location_x; diamond_locations_x];
output_locations_y = [input_location_y; diamond_locations_y];
end

Performing diamond iteration 1 out of 1
Found corner. Continue happening at i = 262144 out of 524288.
Found corner. Continue happening at i = 524288 out of 524288.

Generate an RGB image

function to make input an rgb image. can convert uint 8 to double by using scale = 255.

function image_out = imRGB(image_in,scale)

image_out(:,:,1) = image_in/scale;
image_out(:,:,2) = image_in/scale;
image_out(:,:,3) = image_in/scale;

end


%--------------------------------------

Published with MATLAB® R2020a