Set up and run a heliocentric trajectory simulation with two objects.

Simulation in the gravity field of the Earth, moon, and sun. The spaceraft and asteroid are both treated as objects in the simulation. Both objects use GravityHelio as their default gravity function. The moon is treated as a point mass unless the gravitational harmonics are included in the data structure.

In this demo the thrust vector is always along the Earth relative velocity vector.

See also ForceSimple, PlanetPosJPL, RHSTrajectory, RK4, Plot2D, HelioPlot, GravityHelio

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2017 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2017.1
%--------------------------------------------------------------------------

User inputs

nDays         	 = 80;
dT             	 = 1000; % sec - 2*pi/T must be 10x higher than
                         % the highest harmonic in the system
planets          = [3 10]; % Earth and Moon

% Constants
secInDay         = 86400;
daysInYr         = 365.25;

Initialization

tEnd             = nDays*secInDay;
n                = floor(tEnd/dT);
t                = (0:n-1)*dT;

% Initialize the data structure
d                = RHSTrajectory;
d.jD0            = 2457504.5; % Initial date matching the asteroid state
d.planetID       = planets;

% Object 1 is the spaceraft
d.object(1).mass = 12;

% Object 2 is the asteroid
d.object(2).mass = 5e5;

% Display structure data for user
StructToText(d);

% Initialize the JPL ephemerides
PlanetPosJPL( 'initialize', planets );
[rP,~,vP] = PlanetPosJPL('update', d.jD0);

% Asteroid state from JPL Horizons http://ssd.jpl.nasa.gov/horizons.cgi#top
xA = [ -8.560701547109835E+07; -1.235220355296940E+08; -5.230886882986473E+07;...
        2.336703121935733E+01; -1.445256411364323E+01; -7.005471702678194E+00];

% Spacecraft position and velocity at separation
% For demo purposes, place the spacecraft in GEO orbit
[rO,vO] = El2RV([42000;0;0;0;0;0]);
xS      = [ rP(:,1)+rO;...  % Position (km)
            vP(:,1)+vO];    % Velocity (km/s)
x       = [xS;xA];

% Initialize the state and auxiliary names
RHSTrajectory( x );

object: STRUCTURE ARRAY
object(1).forceModel: STRUCTURE
object(1).forceModel.fun:
	ForceSimple
object(1).forceModel.data: STRUCTURE
object(1).forceModel.data.uThrustECI (3,1):
	1.000000 	0.000000 	0.000000 
object(1).forceModel.data.thrustMag:
	0.01
object(1).mass:
	12
object(1).gravity: STRUCTURE
object(1).gravity.fun:
	GravityHelio
object(1).gravity.data: STRUCTURE
object(1).gravity.data.muSun:
	1.32712e+11
object(1).gravity.data.sphHarmMoon:
	[]
object(1).gravity.data.moonId:
	2
object(1).cM (3,1):
	0.000000 	0.000000 	0.000000 
object(2).forceModel: STRUCTURE
object(2).forceModel.fun:
	NoForce
object(2).forceModel.data:
	[]
object(2).mass:
	500000
object(2).gravity: STRUCTURE
object(2).gravity.fun:
	GravityHelio
object(2).gravity.data: STRUCTURE
object(2).gravity.data.muSun:
	1.32712e+11
object(2).gravity.data.sphHarmMoon:
	[]
object(2).gravity.data.moonId:
	2
object(2).cM (3,1):
	0.000000 	0.000000 	0.000000 
planetID (1,2):
	3.000000 	10.000000 
mu:
	1.32712e+11
jD0:
	2.4575e+06

Run the simulation

n   = length(t);
p   = zeros(24,n);
jD  = d.jD0 + t/86400;

for k = 1:n
  [~,f]         = RHSTrajectory(x,t(k),d);
  p(:,k)        = [x;f.aux];
  [~,~,vP]      = PlanetPosJPL('update', jD(k));
  d.uThrustECI  = Unit(x(4:6)-vP(:,1));
  x             = RK4(@RHSTrajectory,x,dT,t(k),d);
end

Plot results

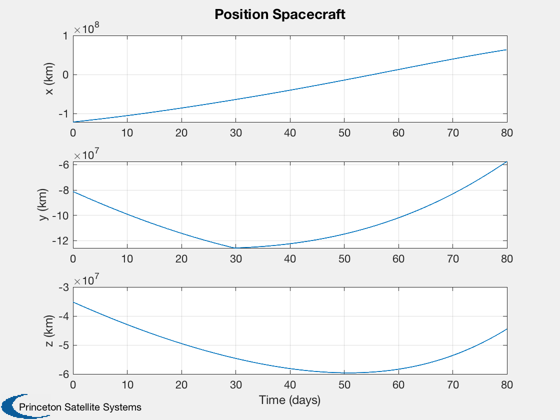
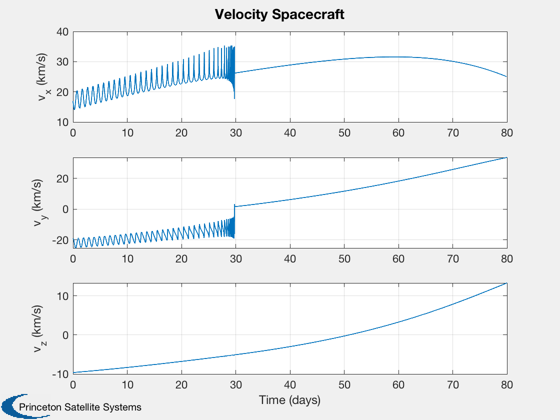
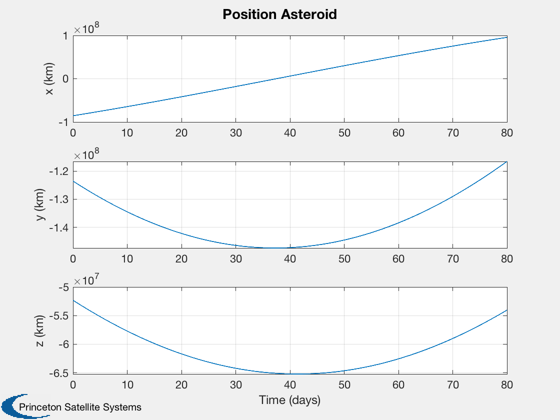
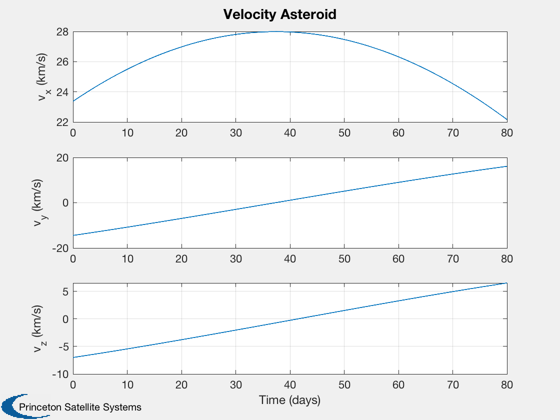
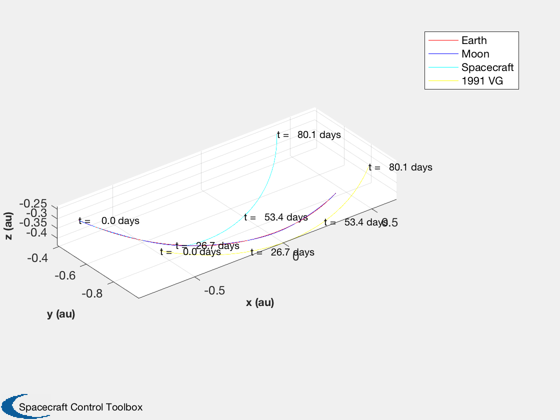
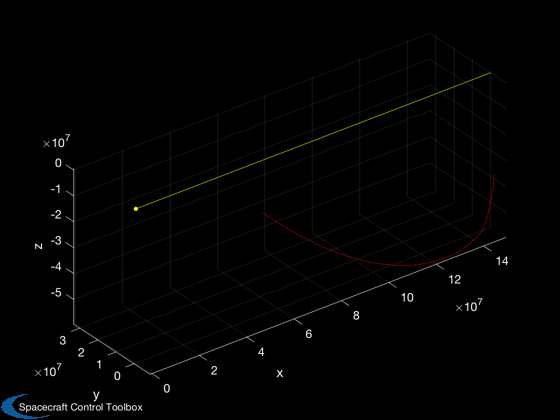
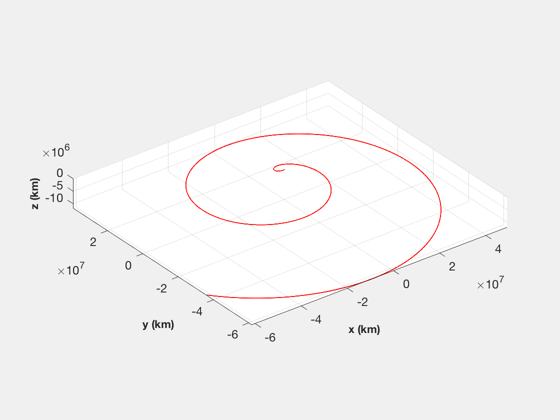
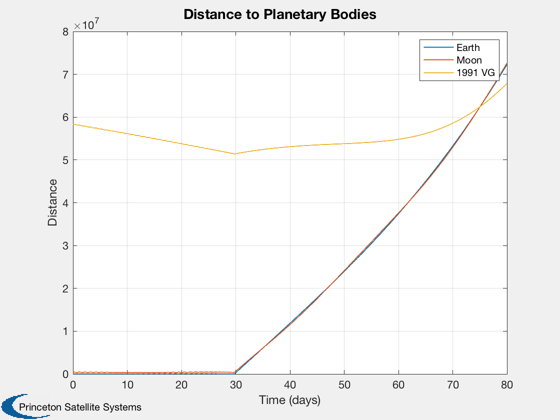
[tt, tL]	= TimeLabl( t );
k         = 1:3;

Plot2D( tt, p(k,:), tL, f.stateNames(k), 'Position Spacecraft');	k = k + 3;
Plot2D( tt, p(k,:), tL, f.stateNames(k), 'Velocity Spacecraft');	k = k + 3;
Plot2D( tt, p(k,:), tL, f.stateNames(k), 'Position Asteroid');    k = k + 3;
Plot2D( tt, p(k,:), tL, f.stateNames(k), 'Velocity Asteroid');    k = k + 3;
Plot2D( tt, p(k,:), tL, f.auxNames(1:3), 'Force');

pName = {'Spacecraft' '1991 VG'};
HelioPlot( d.planetID, nDays/365, d.jD0, p([1:3 7:9],:), pName )

% If the moon is important, plot in various Moon frames
rSEMR = SEMIToSEMR( jD, p(1:3,:), p(4:6,:) );
PlotSEMTraj( rSEMR, 'SEMR', jD );

r_Earth   = p(1:3,:) - p(19:21,:);
r_Moon    = p(1:3,:) - p(22:24,:);
r_ast     = p(1:3,:) - p( 7: 9,:);

EarthMoonRotFrame( r_Earth, jD, [5 5] );
EarthMoon( r_Earth, jD, [5 5] );

Plot2D(tt, [Mag(r_Earth);Mag(r_Moon);Mag(r_ast)], tL, 'Distance','Distance to Planetary Bodies' );
legend('Earth','Moon','1991 VG')

Figui;


%--------------------------------------------------------------------------

Published with MATLAB® R2019a