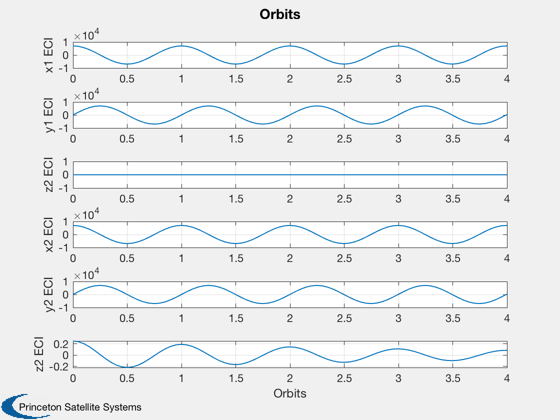
Simulates two orbits and applies a relative controller.

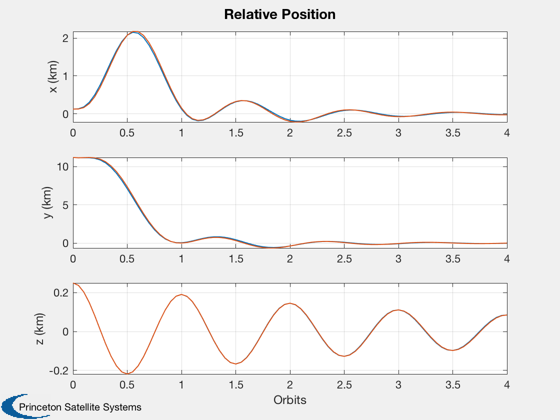
Plots the resulting relative positions. ------------------------------------------------------------------------- See also RelativeOrbitState and LQOrbitController., C2DZOH, QLVLH, QPose, Plot2D, TimeGUI, RK4, JD2000, TOrbit, LinOrb, El2RV, Period, DrawSCPlugIn -------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%	Copyright 1999 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

Clean up the workspace

%----------------------
clear g x1Plot x2Plot x1 x2

Global for the time GUI

%------------------------
global simulationAction
simulationAction = ' ';

View 3D graphics? Takes a lot of memory.

%----------------------------------------
threeDOn = 0;

Constants

%----------
degToRad  = pi/180;
r         = 7000;
p         = Period( r );
n         = 2*pi/p;
dT        = 50;
nSim      = 4*p/dT + 1;

Convert to cartesian

%---------------------
[r1, v1] = El2RV( [7000  0 0 0 0 0] );
[r2, v2] = El2RV( [7000  3.571e-5 -1.57 -1.57 1.7857e-5 3.1416] );
x1       = [r1;v1];
x2       = [r2;v2];
x0       = RelativeOrbitState( x1, x2 );

t  = 0;
jD = JD2000;

Compute the orbit period and controller period

%-----------------------------------------------
dT   = p/20;
nSim = ceil(4*p/dT) + 1;

Compute the orbit controller

%-----------------------------
kOrbitControl = LQOrbitController( x1, [], [], dT );

% 3D
%---
if( threeDOn )
  g(1)                  = load('CubeSat.mat');
  g(2)                  = g(1);
  g(1).name             = 'CubeSat #1';
  g(2).name             = 'CubeSat #2';
  g(1).body(1).bHinge.q = QPose( QLVLH( x1(1:3), x1(4:6) ) );
  g(2).body(1).bHinge.q = QPose( QLVLH( x2(1:3), x2(4:6) ) );
  g(1).rECI             = r1;
  g(1).qLVLH            = g(1).body(1).bHinge.q;
  g(2).rECI             = r2;
  g(2).qLVLH            = g(2).body(1).bHinge.q;
  tag3DWindow           = DrawSCPlugIn( 'initialize', g, [], [], 'Earth', jD );
end

Initialize the time display

%----------------------------
tToGoMem.lastJD        = 0;
tToGoMem.lastStepsDone = 0;
tToGoMem.kAve          = 0;
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, tToGoMem, 0, dT, 'Relative Orbit Control' );

Initialize the arrays

%----------------------
x1Plot    = zeros(6,nSim);
x2Plot    = zeros(6,nSim);
x3Plot    = zeros(6,nSim);
uPlot     = zeros(3,nSim);
dPlot     = zeros(6,nSim);

Disturbances

%-------------
a1            = [0;0;0];
a2            = [0;0;0];
n             = 2*pi/p;
[a, bD, c, d] = LinOrb( [], n );
b             = [0 0;0 0;0 0;0 0;1 0;0 1];
[v, bD]       = C2DZOH( a, bD, dT );
[a, b]        = C2DZOH( a, b,  dT );
xL            = x0;

Generate the two orbits using numerical integration

%----------------------------------------------------
for k = 1:nSim

  % Display the status message
  %---------------------------
  [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT );

  % Control System. The measurements come from the controlling spacecraft
  % and the target spacecraft. The control vector is in track and out-of
  % track for the target orbit.
  %----------------------------------------------------------------------
  [d, y, z]  = RelativeOrbitState( x1, x2 );
  aControl   = -kOrbitControl*d;
  uControl   = y*aControl(1) - z*aControl(2);

  % Plotting
  %---------
  x1Plot(:,k) = x1;
  x2Plot(:,k) = x2;
  x3Plot(:,k) = xL;
  dPlot(:,k)  = d;
  uPlot(:,k)  = uControl;

  % 3D
  %---
  if( threeDOn )

    % Transformation matrices
    %------------------------
    g(1).body(1).bHinge.q = QPose( QLVLH( x1(1:3), x1(4:6) ) );
    g(2).body(1).bHinge.q = QPose( QLVLH( x2(1:3), x2(4:6) ) );
    g(1).rECI             = x1(1:3);
    g(2).rECI             = x2(1:3);
    g(1).qLVLH            = QLVLH( x1(1:3), x1(4:6) );
    g(2).qLVLH            = QLVLH( x2(1:3), x2(4:6) );
    DrawSCPlugIn( 'update spacecraft', tag3DWindow, g, jD );
  end

  % Propagate the orbits
  %---------------------
  x1 = RK4( 'FOrb', x1, dT, t, 'car', a1 );
  x2 = RK4( 'FOrb', x2, dT, t, 'car', a2 + uControl );
  xL = a*xL - b*kOrbitControl*xL;

  % Update the time
  %----------------
  t  =  t + dT;
  jD = jD + dT/86400;

  % Time control
  %-------------
  switch simulationAction
    case 'pause'
      pause
      simulationAction = ' ';
    case 'stop'
      return;
    case 'plot'
      break;
  end
end

This is necessary if the simulation is terminated early

%----------------------------------------------------------
j      = 1:k;
tOrbit = (0:(k-1))*dT/p;

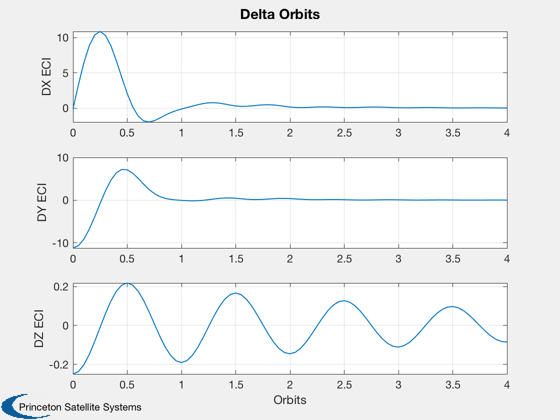
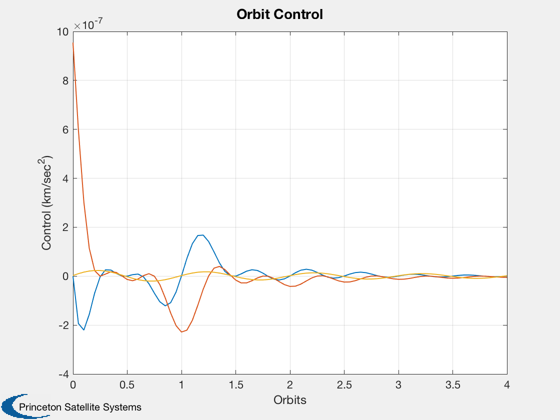
Plotting

%---------
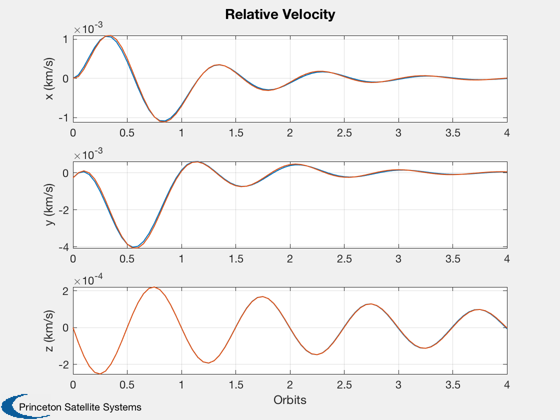
xLbl  = 'Orbits';
yLbl  = ['x1 ECI';'y1 ECI';'z2 ECI';...
         'x2 ECI';'y2 ECI';'z2 ECI'];
yLbl2 = ['DX ECI';'DY ECI';'DZ ECI'];

Plot2D( tOrbit, [x1Plot(1:3,j);x2Plot(1:3,j)],      xLbl, yLbl, 'Orbits' )
Plot2D( tOrbit, [x1Plot(1:3,j)-x2Plot(1:3,j)],      xLbl, yLbl2, 'Delta Orbits' )
Plot2D( tOrbit,  uPlot(:,j),   xLbl, 'Control (km/sec^2)', 'Orbit Control' )
Plot2D( tOrbit,  [dPlot(1:3,j);x3Plot(1:3,j)], xLbl,  ['x (km)';'y (km)';'z (km)'      ],...
    'Relative Position', 'lin', ['[1 4]';'[2 5]';'[3 6]'] )
Plot2D( tOrbit,  [dPlot(4:6,j);x3Plot(4:6,j)], xLbl,  ['x (km/s)';'y (km/s)';'z (km/s)'],...
    'Relative Velocity', 'lin', ['[1 4]';'[2 5]';'[3 6]'] )


%--------------------------------------

Published with MATLAB® R2019a