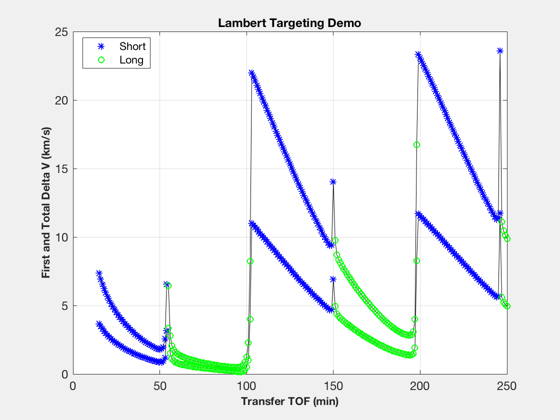
Demonstrates the Lambert targeting function DVTarget.

The selected time of flight drastically affects the resulting delta-V, from 181 m/s to 23 km/sec. ------------------------------------------------------------------------- Reference: Vallado 2nd edition, p.476 and Fig. 7-20 ------------------------------------------------------------------------- See also Plot3D, TitleS, XLabelS, YLabelS, Mag, DVTarget, LambertTOF, RV2El, RVFromKepler -------------------------------------------------------------------------

Also plot a sample trajectory pair

%--------------------------------------------------------------------------
%	 Copyright 2003 Princeton Satellite Systems, Inc. All rights reserved.
%--------------------------------------------------------------------------

% Initial spacecraft states at epoch
r1 = [5328.7862; 4436.1273; 101.4720];
v1 = [-4.864779; 5.816486; .240163];
r2 = [6697.4756; 1794.5831; 0];
v2 = [-1.962372; 7.323674; 0];
disp('Current Elements [a i W w e M] :')
disp(RV2El(r1,v1))
disp('Target Elements:')
disp(RV2El(r2,v2))

% Transfer times and plotting parameters
tTrans = [15:1:250]*60;
aPlot  = zeros(size(tTrans));
bPlot  = zeros(size(tTrans));
tMPlot = bPlot;

% Perform targeting
for k = 1:length(tTrans)
  [dV,tM,ok] = DVTarget(r1,v1,r2,v2,tTrans(k));
  aPlot(k)   = Mag( dV.a );
  bPlot(k)   = aPlot(k) + Mag( dV.b );
  tMPlot(k)  = tM;
  if ~ok
    tMPlot(k) = 0;
  end
end

% Generate plot
kShort = find(tMPlot>0);
kLong  = find(tMPlot<0);
kEarth = find(tMPlot==0);
NewFig('TargetDemo');
plot(tTrans/60,[aPlot;bPlot],'k');
hold on
hS = plot(tTrans(kShort)/60,[aPlot(kShort);bPlot(kShort)],'b*');
hL = plot(tTrans(kLong)/60,[aPlot(kLong);bPlot(kLong)],'go');
hE = plot(tTrans(kEarth)/60,[aPlot(kEarth);bPlot(kEarth)],'rs');
legend([hS(1) hL(1)],'Short','Long','location','best');
XLabelS('Transfer TOF (min)');
YLabelS('First and Total Delta V (km/s)');
TitleS('Lambert Targeting Demo');
grid on;

Current Elements [a i W w e M] :
       6943.2     0.034906       0.2618       1.3963    0.0022324     -0.95994
Target Elements:
       6933.7            0            0       5.8152   8.5654e-08      0.72978

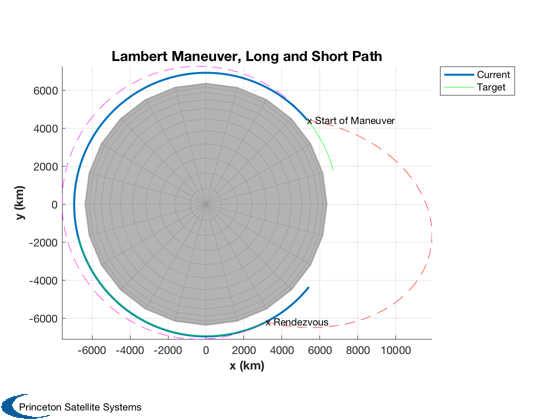
Also plot a sample trajectory pair

%-----------------------------------
tTrans = 75*60;
% initial orbits
[r1p,v1p] = RVFromKepler(RV2El(r1,v1),linspace(0,tTrans));
[r2p,v2p] = RVFromKepler(RV2El(r2,v2),linspace(0,tTrans));
% first transfer
vTrans = LambertTOF( r1, r2p(:,end), tTrans, 1 );
rT1 = RVFromKepler(RV2El(r1,vTrans(:,1)),linspace(0,tTrans));
% second transfer
[vTrans,a,p] = LambertTOF( r1, r2p(:,end), tTrans, -1 );
[rT2,v] = RVFromKepler(RV2El(r1,vTrans(:,1)),linspace(0,tTrans));

[h,h1] = Plot3D( r1p, 'x (km)','y (km)','z (km)', 'Lambert Maneuver, Long and Short Path', 6378 );
hold on;
h2 = plot3(   r2p(1,:),   r2p(2,:),   r2p(3,:), 'g');
plot3(   rT1(1,:),   rT1(2,:),   rT1(3,:), 'r--');
plot3(   rT2(1,:),   rT2(2,:),   rT2(3,:), 'm--');
text( r1(1,1),  r1(2,1),  r1(3,1), 'x Start of Maneuver')
text( rT2(1,end),  rT2(2,end),  rT2(3,end), 'x Rendezvous')
axis square; axis equal;
view(0,90);
legend( [h1 h2], 'Current', 'Target' )

%--------------------------------------
% PSS internal file version information
%--------------------------------------

Demonstrates the Lambert targeting function DVTarget.

Contents

Also plot a sample trajectory pair