Demonstrate a Hohmann Transfer in simulation

The spacecraft has 3 reaction wheels and a single thruster that needs to be aligned with the velocity vector for the burns. The delta-V is computed with OrbMnvrHohmann, and the propellant mass is then computed using RocketMass. The fuel mass is then used to compute the duration of the finite burn. A numerical simulation implements the necessary attitude and orbit

-------------------------------------------------------------------------
See also: Mag, RV2El, Period, OrbMnvrHohmann, RocketMass, InertiaCubeSat,
RHSRWAOrbit, PID3Axis, RK4, TimeHistory, Figui
-------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 2022 Princeton Satellite Systems, Inc.
%   All rights reserved.
%   Since version 2022.1
%-------------------------------------------------------------------------------

Constants

nToKN    = 0.001;
mu       = Constant('mu earth');

Compute the maneuver

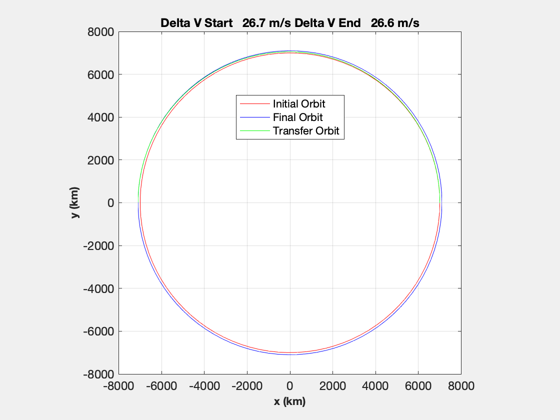
rI       = [-7000;0;0];
vI       = [0;-sqrt(mu/Mag(rI));0];
rF       = 7100;
el       = RV2El(rI,vI);
p        = Period(el(1));
OrbMnvrHohmann(Mag(rI),rF);
[dV,tOF] = OrbMnvrHohmann(Mag(rI),rF);

Hohmann Transfer
------------------------------------------------
Initial Orbit Radius      =    7000.0000
Final Orbit Radius        =    7100.0000
------------------------------------------------
Delta V Total             =       0.0533
Delta V at A              =       0.0267
Delta V at B              =       0.0266
E transfer                =       0.0071
SMA transfer              =    7050.0000
Time of Flight            =       0.8182 hours

Set up the spacecraft

mP       = 6; % kg
thrustE  = 4.448*0.2; % N
dVTot    = dV.a + dV.b; % km/s
iSp      = 224; % s
fS       = 0.1; % Structural fraction
[mF,mT]  = RocketMass(iSp,mP,fS,dVTot);
inr      = InertiaCubeSat('6U',mT);
acc      = thrustE/mT; % m/s^2
tBA      = dV.a/acc/nToKN; % s
tBB      = dV.b/acc/nToKN; % s
dRHS     = RHSRWAOrbit;
dRHS.inr = inr;
dRHS.m   = mT;
tStart   = [p/4-tBA/2 p/4+tOF-tBB/2]; % center burn durations on target timehelp
tEnd     = tStart + [tBA tBB];

Set up the controller

dC             = PID3Axis;
dC.body_vector = [1;0;0];
dC.mode        = 1; % Align two axes
dC.inertia     = inr;

fprintf('Burn A duration %8.2f s\n',tBA);
fprintf('Burn B duration %8.2f s\n',tBB);
fprintf('Thrust          %8.2f N\n',thrustE);
fprintf('Mass Total      %8.2f kg\n',mT);
fprintf('Mass Fuel       %8.2f kg\n',mF);
fprintf('Initial SMA     %8.2f km\n',el(1));
fprintf('Initial e       %8.2f\n',el(5));

Burn A duration   185.04 s
Burn B duration   184.39 s
Thrust              0.89 N
Mass Total          6.16 kg
Mass Fuel           0.15 kg
Initial SMA      7000.00 km
Initial e           0.00

Steps

1. Reorient with reaction wheels 2. Burn 3. Reorient/coast 4. Burn

Simulation

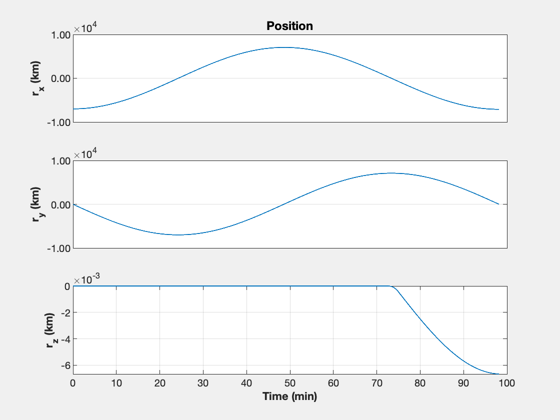
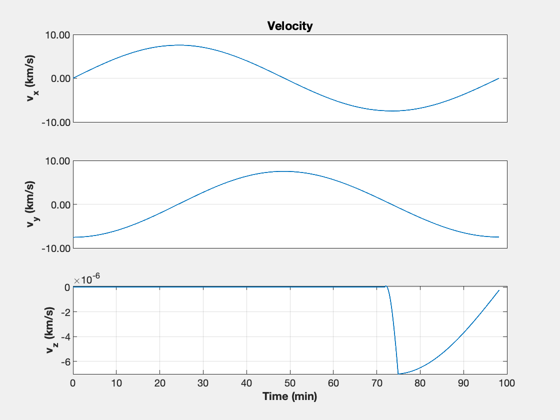
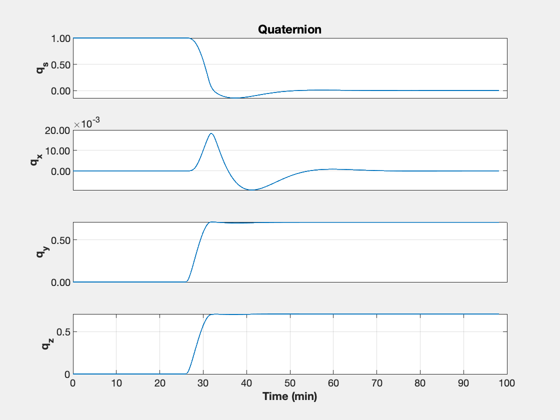
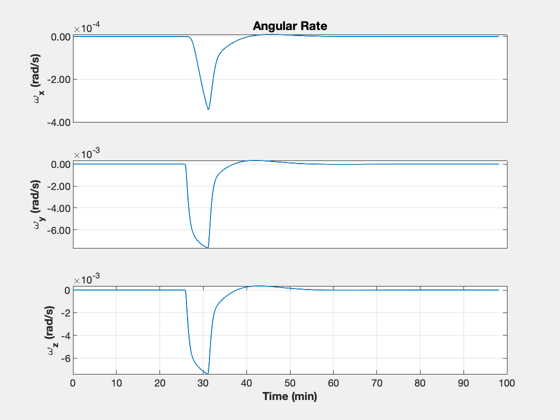
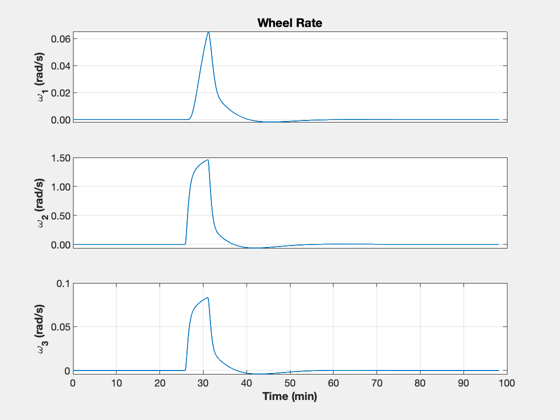
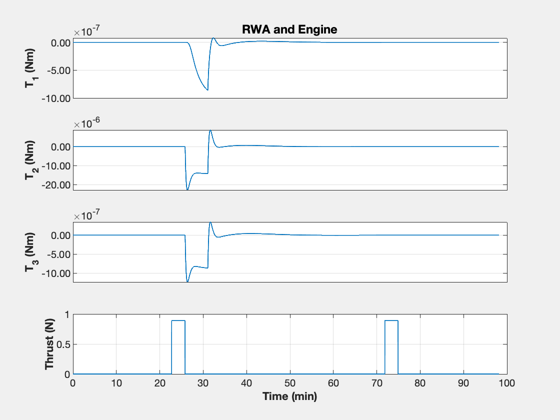
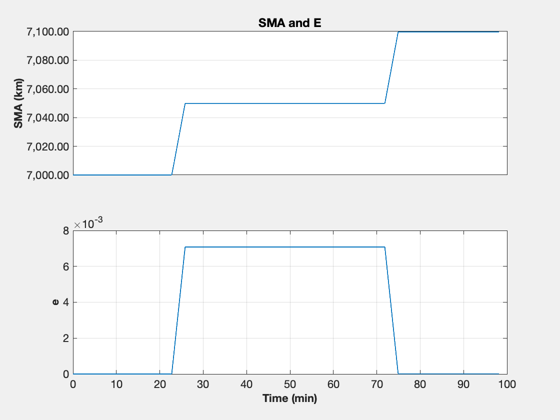
% ECI burn vector
uBurn  = [1 -1;0 0;0 0];
dT     = 1; % s
n      = ceil(2*tOF/dT);
kMnvr  = 1;
x      = [rI;vI;1;zeros(9,1)];
xP     = zeros(22,n);
inMnvr = false;
t      = (0:n-1)*dT;

aDone  = false;
bDone  = false;

% Simulation loop
for k = 1:n
  % Update the controller
  dC.eci_vector = uBurn(:,kMnvr);
  [tRWA, dC]    = PID3Axis( x(7:10), dC );

  % Start the first burn
  inMnvr = false;
  if( t(k) > tStart(1) && t(k) < tEnd(1) )
    inMnvr = true;
  end

  % Switch orientation
  if( t(k) > tEnd(1) )
    kMnvr = 2;
  end

  % Start the second burn
  if( t(k) > tStart(2) && t(k) < tEnd(2) )
    inMnvr = true;
    kMnvr  = 2;
  end

  if( inMnvr )
    dRHS.force = thrustE*QTForm(x(7:10),dC.body_vector)*nToKN; % kN
  else
    dRHS.force = [0;0;0];
  end
  el = RV2El(x(1:3),x(4:6));
  xP(:,k) = [x;tRWA;Mag(dRHS.force)/nToKN;el(1);el(5)];

  % Right hand side
  dRHS.torqueRWA = -tRWA;
  x = RK4(@RHSRWAOrbit,x,dT,0,dRHS);
end

fprintf('Final SMA       %8.2f km\n',el(1));
fprintf('  SMA error     %8.2f km\n',rF-el(1));
fprintf('Final e         %8.2g\n',el(5));

yL = {'r_x (km)' 'r_y (km)' 'r_z (km)' ...
      'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)' ...
      'q_s' 'q_x' 'q_y' 'q_z' ...
      '\omega_x (rad/s)' '\omega_y (rad/s)' '\omega_z (rad/s)' ...
      '\omega_1 (rad/s)' '\omega_2 (rad/s)' '\omega_3 (rad/s)' ...
      'T_1 (Nm)' 'T_2 (Nm)' 'T_3 (Nm)' ...
      'Thrust (N)' 'SMA (km)' 'e'};

k = 1:3;
TimeHistory(t,xP(k,:),yL(k),'Position');
k = 4:6;
TimeHistory(t,xP(k,:),yL(k),'Velocity');
k = 7:10;
TimeHistory(t,xP(k,:),yL(k),'Quaternion');
k = 11:13;
TimeHistory(t,xP(k,:),yL(k),'Angular Rate');
k = 14:16;
TimeHistory(t,xP(k,:),yL(k),'Wheel Rate');
k = 17:20;
TimeHistory(t,xP(k,:),yL(k),'RWA and Engine');
k = 21:22;
TimeHistory(t,xP(k,:),yL(k),'SMA and E');

Figui;


%--------------------------------------

Final SMA        7099.72 km
  SMA error         0.28 km
Final e          1.3e-05

Published with MATLAB® R2021b