Orbit separation simulation with discrete delta-Vs

Simulates a discrete phasing maneuver in the absolute frame. Includes a simple drag model and point-mass gravity. The simulation runs for twice the desired transfer time.

Contents

%-------------------------------------------------------------------------------
%	Copyright 2017 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------
%   Since version 2017.1
%--------------------------------------------------------------------------

Constants and Parameters

%--------------------------
sma  = 6740;    % km
inc  = 0;       % inclination
dSep = 20;      % km
jD0  = JD2000;
tTrans = 60*60; % s
thrust = 5;     % N
mass   = 12;    % kg
degToRad  = pi/180;
mu        = 3.9860046e5;
useDrag   = false;

Initialize the data

%---------------------
[r1,v1]   = El2RV( [sma inc 0 0 0 0], [], mu);
[r2,v2]   = El2RV( [sma inc 0 0 0 0], [], mu);
delTheta  = dSep/sma;
elT       = [sma inc 0 0 0 -delTheta];
[rT,vT]   = El2RV(elT, [], mu);
dV        = DVTarget(r1,v1,rT,vT,tTrans);
dVa       = dV.a*1e3;
dVb       = dV.b*1e3;
dVMag     = Mag(dVa)+Mag(dVb);
tBurn     = dVMag/2*mass/thrust;
Porb      = Period(sma);
dTSim     = Porb/300;
tOrbit    = 0:dTSim:2*tTrans;
nSim      = length(tOrbit);
fprintf('Total delta-V for maneuver: %g m/s\n',dVMag);
fprintf('Thrust: %g N\n',thrust);
fprintf('Burn time per maneuver: %g s\n',tBurn);

% Initial state
x1        = [r1;v1];
x2        = [r2;v2];
t         = 0;

% Initialize the arrays
%----------------------
x1Plot    = zeros(6,nSim);
x2Plot    = zeros(6,nSim);
d1Plot    = zeros(3,nSim);
d2Plot    = zeros(3,nSim);

Total delta-V for maneuver: 6.53174 m/s
Thrust: 5 N
Burn time per maneuver: 7.83809 s

Generate the two orbits using numerical integration

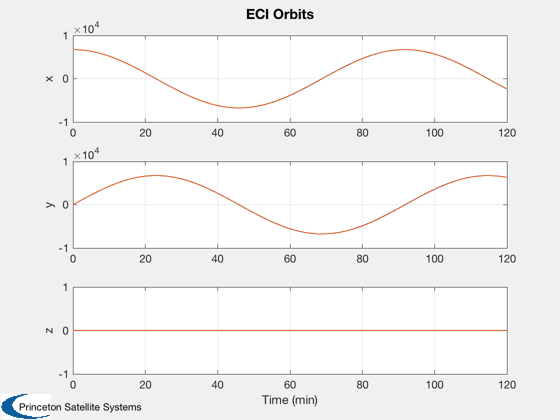
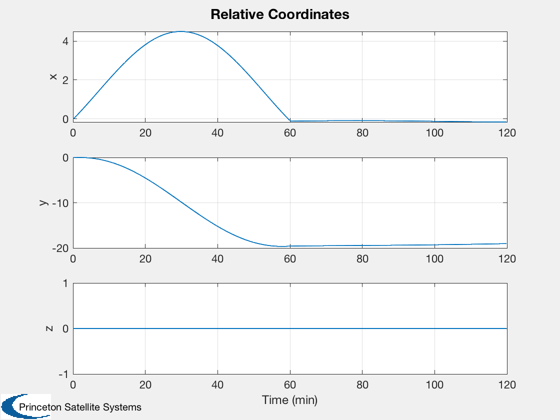
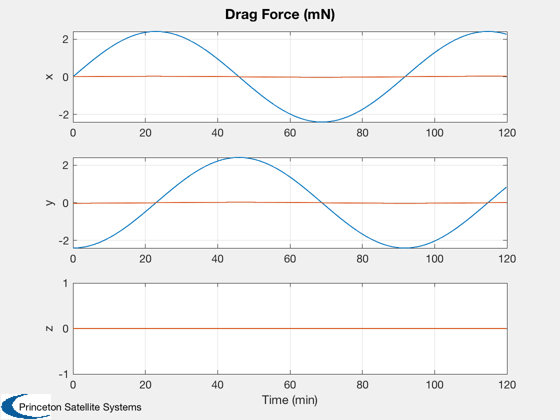
nBurn     = ceil(tBurn/dTSim);
f         = tBurn/(nBurn*dTSim);
acc       = thrust/mass*1e-3; % km/s2
accels    = zeros(3,nSim);
tP        = floor(tTrans/dTSim);
for k = 1:nBurn
  accels(:,k) = f*acc*Unit(dV.a);
  accels(:,tP+k) = f*acc*Unit(dV.b);
end
kOn = (Mag(accels)~=0);

for k = 1:nSim
  % Plotting
  %---------
  x1Plot(:,k) = x1;
  x2Plot(:,k) = x2;

  % Calculate drag disturbance
  area = [5; 0.06];
  d1 = AeroDragForce( x1, area(1) );
  d2 = AeroDragForce( x2, area(2) );
  d1Plot(:,k) = d1;
  d2Plot(:,k) = d2;
  if ~useDrag
    d1 = 0*d1;
    d2 = 0*d2;
  end

  % Propagate the orbits
  %---------------------
  x1 = RK4( @FOrb, x1, dTSim, t, 'car', d1*1e-3/mass, mu );
  x2 = RK4( @FOrb, x2, dTSim, t, 'car', d2*1e-3/mass+accels(:,k), mu );

  % Update the time
  %----------------
  t  =  t + dTSim;
  jD = jD0 + dTSim/86400;

end

% Relative coordinates
r1 = x1Plot(1:3,:);
v1 = x1Plot(4:6,:);
r2 = x2Plot(1:3,:);
d  = RelativeCoord( r1, v1, r2 );

Plotting

%---------
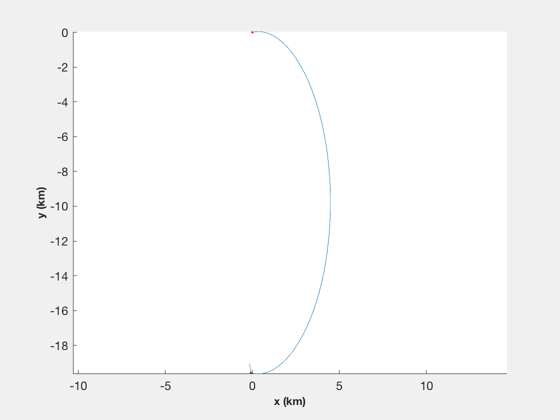
Plot2D( tOrbit/60, [r1; r2], 'Time (min)', {'x','y','z'}, 'ECI Orbits',...
  'lin',{[1 4],[2 5],[3 6]});
Plot2D( tOrbit/60, d, 'Time (min)', {'x','y','z'}, 'Relative Coordinates');

Plot2D( tOrbit/60, [d1Plot; d2Plot]*1e3, 'Time (min)', {'x','y','z'}, 'Drag Force (mN)',...
  'lin',{[1 4],[2 5],[3 6]});

NewFig('Relative Orbit 3D')
plot3( d(1,:), d(2,:) ,d(3,:) )
grid
XLabelS('x (km)')
YLabelS('y (km)')
ZLabelS('z (km)')
view(0,90)
hold on
iOn = find(kOn);
plot3( d(1,iOn), d(2,iOn) ,d(3,iOn),'r.' )
axis equal


%--------------------------------------

grid =
     0     0     1     0     0     0     1     0
     0     0     0     1     0     1     0     0
     0     0     0     0     0     0     0     0
     0     0     0     0     0     1     1     0
     0     0     0     0     0     0     0     1
     0     0     0     0     0     0     0     0
     0     0     0     0     0     1     0     0
     0     1     0     0     0     1     1     1

Published with MATLAB® R2019a