Orbit separation demo

Calculate a delta-V for an in-plane separation and size a thruster to perform the maneuver. This is a bang/bang maneuver.

This demonstrates that a small satellite deployed in LEO can move 1 km away from the "mother ship" in less than one orbit with a range of thrusters. The Lambert delta-V approaches the ideal delta-V as the time approaches one orbit.

Contents

%--------------------------------------------------------------------------
%	Copyright 2017 Princeton Satellite Systems, Inc. All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2017.1
%--------------------------------------------------------------------------

Parameters and ideal solution

% Mission Parameters
sma = 6740; % km
dSep = 20;   % km
mass = 12;  % kg

% Ideal delta-V for 1 revolution. This function can also calculate DVs for
% multiple revolutions.
nRev = 1;
dVPhase = OrbMnvrPhaseChange( sma, dSep/sma, nRev )*1e3;
fprintf(1,'1 Rev Delta-V: %f m/s\n',dVPhase);

1 Rev Delta-V: 2.420097 m/s

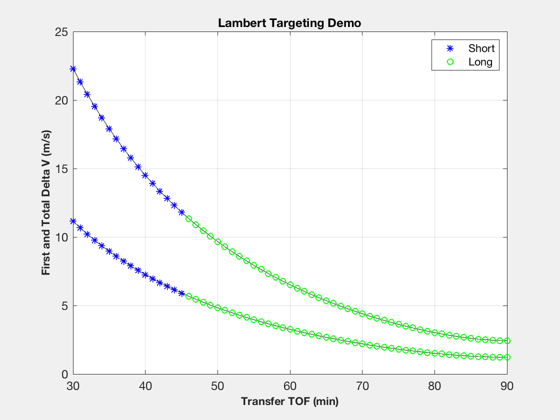
Lambert delta-V study

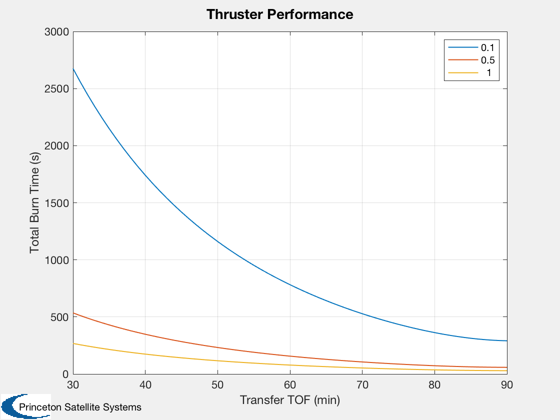
Study a single-revolution Lambert maneuver to achieve the phase change. Then, determine how long the thruster(s) would need to fire to achieve the delta-V.

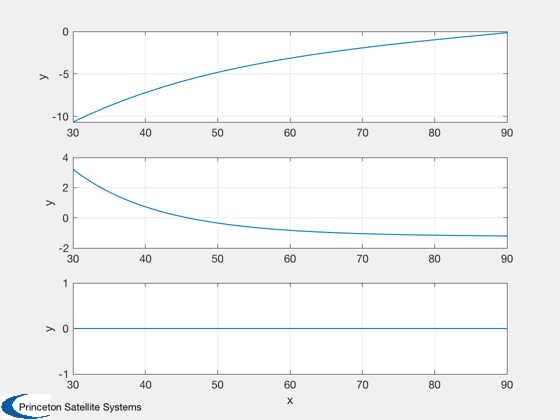
thrusts = [0.1;0.5;1]; % N

% Initial orbit
el = [6740 0 0 0 0 0];
[r1,v1] = El2RV(el);

% Target - 1 km trailing separation
delTheta = dSep/sma;
elT = [6740 0 0 0 0 delTheta];
[r2,v2] = El2RV(elT);

% Transfer times and plotting parameters
% Do NOT go more than one revolution.
tTrans = [30:90]*60;
dVa  = zeros(3,size(tTrans,2));
dVb  = zeros(3,size(tTrans,2));
tMPlot = zeros(size(tTrans));

% Perform targeting
for k = 1:length(tTrans)
  [dV,tM,ok] = DVTarget(r1,v1,r2,v2,tTrans(k));
  dVa(:,k)   = dV.a*1e3;
  dVb(:,k)   = dV.b*1e3;
  tMPlot(k)  = tM;
end

aMag = Mag(dVa);
bMag = aMag + Mag(dVb);

Plot2D(tTrans/60,dVa)

% Generate plot
kShort = find(tMPlot>0);
kLong  = find(tMPlot<0);
kEarth = find(tMPlot==0);
NewFig('Delta V');
plot(tTrans/60,[aMag;bMag],'k');
hold on
hS = plot(tTrans(kShort)/60,[aMag(kShort);bMag(kShort)],'b*');
if ~isempty(kLong)
  hL = plot(tTrans(kLong)/60,[aMag(kLong);bMag(kLong)],'go');
  legend([hS(1) hL(1)],'Short','Long');
end
XLabelS('Transfer TOF (min)');
YLabelS('First and Total Delta V (m/s)');
TitleS('Lambert Targeting Demo');
grid on;

fprintf(1,'Minimum Lambert Delta-V: %f m/s\n',min(bMag));

% Estimate manuever time vs. thrust; assume constant mass
deltaT = mass*(1./thrusts)*bMag;
Plot2D(tTrans/60,deltaT,'Transfer TOF (min)','Total Burn Time (s)','Thruster Performance')
legend(num2str(thrusts))

Minimum Lambert Delta-V: 2.424115 m/s

Plot ideal transfer

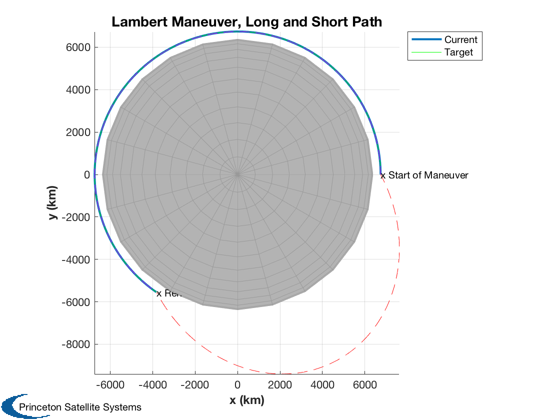
The long and short way computed by the Lambert algorithm are both shown for clarify, but DVTarget automatically chooses the one with the lowest delta-V.

tTrans = 60*60; % long way (greater than pi mean anomaly change)
[dV,tM,ok] = DVTarget(r1,v1,r2,v2,tTrans);

% Initial orbits
[r1p,v1p] = RVFromKepler(RV2El(r1,v1),linspace(0,tTrans));
[r2p,v2p] = RVFromKepler(RV2El(r2,v2),linspace(0,tTrans));
% first transfer
[vTrans,a,p] = LambertTOF( r1, r2p(:,end), tTrans, 1 );
[rT1,v] = RVFromKepler(RV2El(r1,vTrans(:,1)),linspace(0,tTrans));
% second transfer
[vTrans,a,p] = LambertTOF( r1, r2p(:,end), tTrans, -1 );
[rT2,v] = RVFromKepler(RV2El(r1,vTrans(:,1)),linspace(0,tTrans));

[h,h1] = Plot3D( r1p, 'x (km)','y (km)','z (km)', 'Lambert Maneuver, Long and Short Path', 6378 );
hold on;
h2 = plot3(   r2p(1,:),   r2p(2,:),   r2p(3,:), 'g');
plot3(   rT1(1,:),   rT1(2,:),   rT1(3,:), 'r--');
plot3(   rT2(1,:),   rT2(2,:),   rT2(3,:), 'm--');
text( r1(1,1),  r1(2,1),  r1(3,1), 'x Start of Maneuver')
text( rT2(1,end),  rT2(2,end),  rT2(3,end), 'x Rendezvous')
axis square; axis equal;
view(0,90);
legend( [h1 h2], 'Current', 'Target' )


%--------------------------------------

Published with MATLAB® R2019a