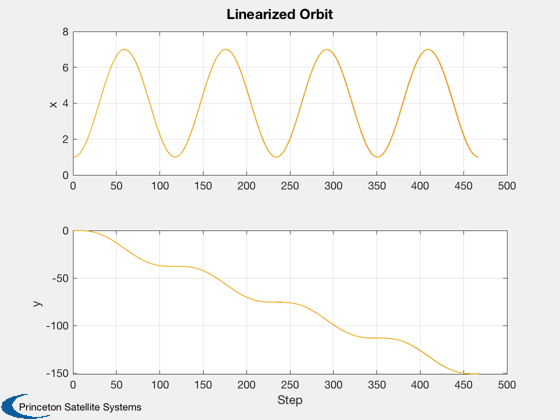
Linear orbit simulation. This compares nonlinear with linear.

In addition it computes the analytical solution for the linearized equations.
------------------------------------------------------------------------
See also C2DZOH, Plot2D, RK4, CylOrb2Cart, RelativeOrbitState, LinOrb,
El2RV, Period
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 1999 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

sMA       = 7000;
[r1,v1]   = El2RV( [sMA 0 0 0 0 0 ]);
p         = Period( sMA );
n         = 2*pi/p;
dT        = 50;
nSim      = 4*p/dT + 1;

The linearized orbit

%---------------------
[a,b,c,d] = LinOrb([],n);
[a,b]     = C2DZOH( a, b, dT );

The linearized orbit state

%---------------------------
x0  = [1;0;0;0;0;0];

Write the intial state in cylindrical coordinates

%--------------------------------------------------
x1 = [7000;0;0;0;n;0];
x2 = x1 + x0;

Convert to cartesian

%---------------------
x1 = CylOrb2Cart( x1 );
x2 = CylOrb2Cart( x2 );

t     = 0;
x     = x0;
xPlot = [];
for k = 1:nSim
  s          = sin(n*t);
  c          = cos(n*t);
  xA         = 2*x0(4)*s/n - (2*x0(5)/n + 3*x0(1))*c + (2*x0(5)/n + 4*x0(1));
  yA         = 2*x0(4)*c/n + (4*x0(5)/n + 6*x0(1))*s + (x0(2) - 2*x0(4)/2) - (3*x0(5) + 6*n*x0(1))*t;
  d          = RelativeOrbitState( x1, x2 );
  xPlot(:,k) = [x(1:2);xA;yA;d(1);d(2)];
  x          = a*x;

  % Propagate the orbits
  %---------------------
  x1         = RK4( 'FOrb', x1, dT, t, 'car' );
  x2         = RK4( 'FOrb', x2, dT, t, 'car' );
  t          = t + dT;
end

Plot2D(1:nSim,xPlot(1:6,:),'Step',['x ';'y ';],'Linearized Orbit','lin',['[1 3 5]';'[2 4 6]'])

%--------------------------------------

Published with MATLAB® R2019a