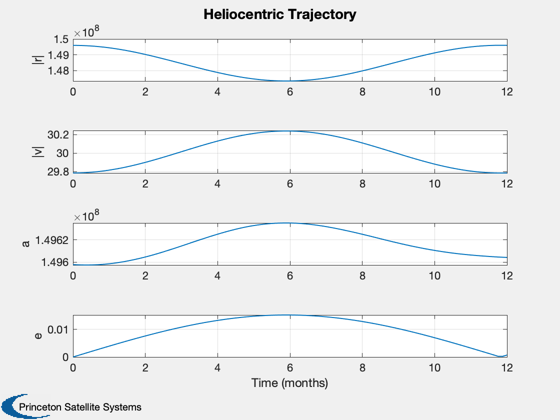
Orbit simulation of a solar sail.

------------------------------------------------------------------------
See also Plot2D, TimeGUI, TimeLabl, Mag, Unit, Date2JD, RV2AE,
PlanetPosition
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%    Copyright (c) 2006 Princeton Satellite Systems, All rights reserved.
%-------------------------------------------------------------------------------

clear d;

Globals for the GUI

%--------------------
global simulationAction
simulationAction = ' ';

d.muSun           = 1.327124e+11;

Solar sail. The normal is defined in the heliocentric system.

%--------------------------------------------------------------
d.sail.normal     = [1;0;0];
d.sail.area       = 100^2;
d.sail.sigmaT     = 0;
d.sail.sigmaA     = 1.0;
d.sail.sigmaD     = 0.0;
d.sail.sigmaS     = 0.0;
d.mass            = 1000;
d.planetsOn       = 1;

d.jDStart         = Date2JD; % Today

The number of steps

%--------------------
nSim          = 100;

Initialize the planet function

%-------------------------------
PlanetPosition('initialize',1:9); % All 9 planets

Create the time array

%----------------------
tDuration     = 86400*365.25;
t             = linspace(0,tDuration);
dT            = t(2) - t(1);

Specify the ode113 accuracy

%----------------------------
xODEOptions   = odeset( 'AbsTol', 1e-4, 'RelTol', 1e-4 );

Set up the position and velocity vectors. Units are km and km/s.

%-----------------------------------------------------------------
a0            = 149597870;
r             = [a0;0;0];
v             = [0;sqrt(d.muSun/a0);0];

Assemble the state vector

%--------------------------
x             = [r;v];

Initialize the time display

%----------------------------
dTSim                  = dT;
tToGoMem.lastJD        = 0;
tToGoMem.lastStepsDone = 0;
tToGoMem.kAve          = 0;
ratioRealTime          = 0;
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, tToGoMem, 0, dT, 'Heliocentric Mars Transfer' );

xPlot      = zeros(8,nSim);
[a,e]      = RV2AE( x(1:3), x(4:6), d.muSun );
xPlot(:,1) = [x;a;e];

Simulate

%---------
for k = 2:nSim
	% Display the status message
	%---------------------------
	[ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT );

	% Keep the sail normal aligned with the position vector
	%------------------------------------------------------
	d.sail.normal = -Unit(x(1:3));

	% Propagator
	%-----------
	[z, x]        = ode113( 'FSolarSail', [t(k-1) t(k)], x, xODEOptions, d );
	x             = x(end,:)';
	[a,e]         = RV2AE( x(1:3), x(4:6), d.muSun );
	xPlot(:,k)    = [x;a;e];


	% User controls on the GUI
	%-------------------------
	switch simulationAction
    	case 'pause'
      		pause
      		simulationAction = ' ';
    	case 'stop'
	  		dontPlot = 1;
      		break;
    	case 'plot'
     		break;
  	end
end

Close the time GUI

%-------------------
close( tToGoMem.hGUI.fig );

j = 1:k;
r = Mag(xPlot(1:3,j));
v = Mag(xPlot(4:6,j));

Visualize the orbit

%--------------------
[t, c] = TimeLabl( t(j) );
Plot2D( t, [r;v;xPlot(7:8,j)], c, ['|r|';'|v|';' a ';' e '], 'Heliocentric Trajectory' );

dV        = xPlot(7,k);
tDuration = t(end);

%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2020a