Simulate an orbit using the variational equations.

Since version 1.
------------------------------------------------------------------------
See also Plot2D, RK4, El2Eq
------------------------------------------------------------------------

Initial elements

%-------------------------------------------------------------------------------
%	 Copyright 1994 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

Initial elements

%-----------------
a = 7000;
i = 5*pi/180;
W = 0;
w = 0;
e = 0.001;
M = 0;

el = [a,i,W,w,e,M]
eq = El2Eq( el )
aT = [0;0;0.000001];

nSim = 100;
xQT = [eq', zeros(6,nSim-1)];
xQP = [eq', zeros(6,nSim-1)];
xLT = [el', zeros(6,nSim-1)];
xLP = [el', zeros(6,nSim-1)];

dT = 1000;

for k = 2:nSim
  xQT(:,k) = RK4( 'FVarEq', xQT(:,k-1), dT, 0, 'eqt', aT );
  xQP(:,k) = RK4( 'FVarEq', xQP(:,k-1), dT, 0, 'eqp', aT );
  xLT(:,k) = RK4( 'FVarEq', xLT(:,k-1), dT, 0, 'elt', aT );
  xLP(:,k) = RK4( 'FVarEq', xLT(:,k-1), dT, 0, 'elp', aT );
end

t = dT*(0:(nSim-1));

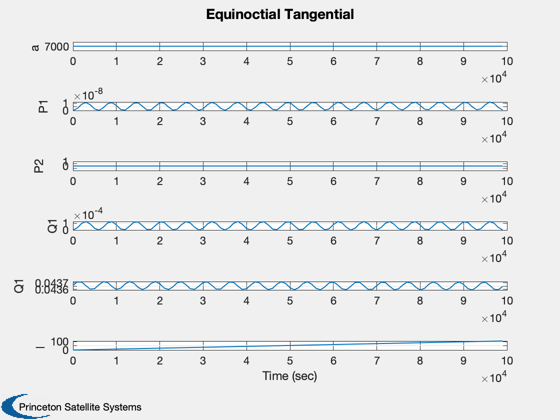
Plot2D( t, xQT,'Time (sec)',['a ';'P1';'P2';'Q1';'Q1';'l '],'Equinoctial Tangential')
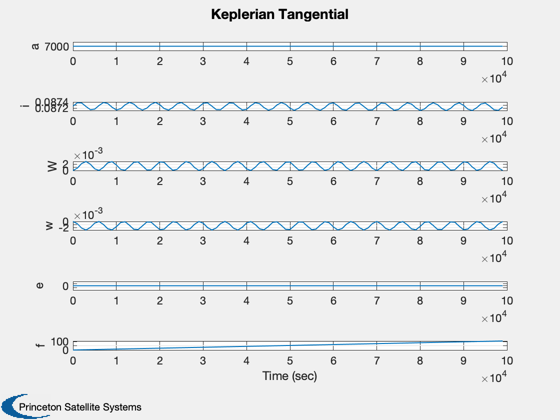
Plot2D( t, xLT,'Time (sec)',['a';'i';'W';'w';'e';'f'],      'Keplerian Tangential')

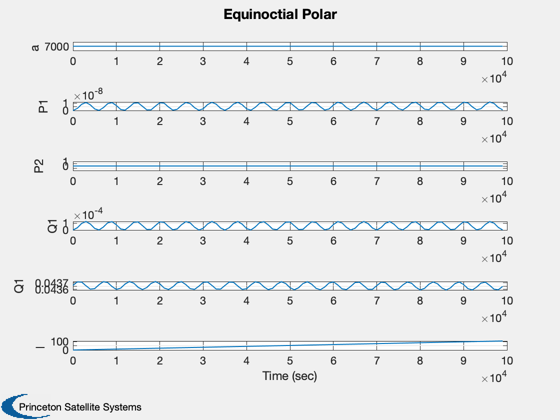
Plot2D( t, xQP,'Time (sec)',['a ';'P1';'P2';'Q1';'Q1';'l '],'Equinoctial Polar')
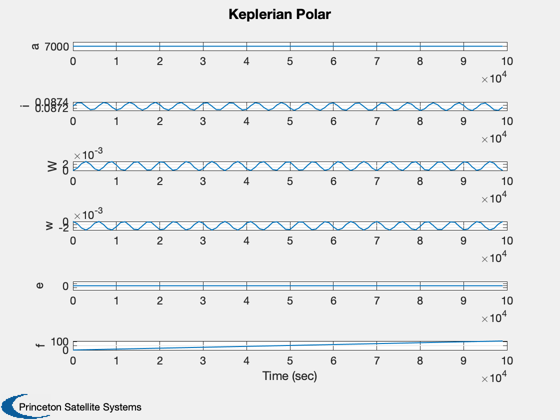
Plot2D( t, xLP,'Time (sec)',['a';'i';'W';'w';'e';'f'],      'Keplerian Polar')


%-------------------------------------------------------------------------------
% PSS internal file version information
%--------------------------------------

el =
         7000     0.087266            0            0        0.001            0
eq =
         7000            0        0.001            0     0.043661            0

Simulate an orbit using the variational equations.

Contents

Initial elements