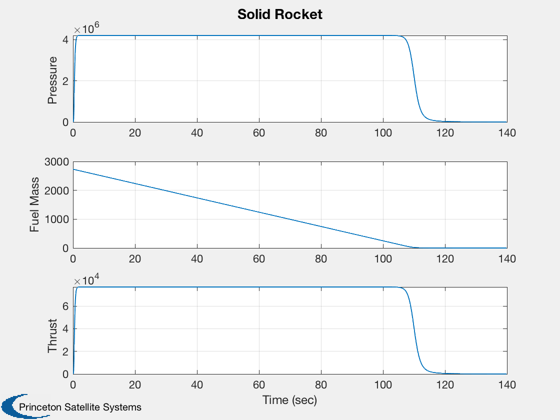
Demonstrate a solid rocket motor.

This integrates using Euler integration.

------------------------------------------------------------------------
See also SolidR, TCoeff. and Plot2D
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 1995 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------
%   Since version 1.
%-------------------------------------------------------------------------------

Constants

%----------
inToM         = 1/39.37;
lbToKg        = 1/2.205;
lbPIn3ToKgPM3 = lbToKg*39.37^3;
fToC          = 5/9;
lbFToN        = 4.448;
psiToNm2      = 6895;

Solid Rocket Parameters for the Orbus-6 IUS

%--------------------------------------------
rM    = (63.3-0.35)*inToM;                   % Propellant outside radius
rhoP  = 0.0635*lbPIn3ToKgPM3;                % Propellant density
n     = 0.45;                                % Pressure coefficient
a     = 0.276*inToM/(1000*psiToNm2)^n;       % Burning rate constant
sigP  = 0;                                   % Burning rate temperature sensitivity coefficient
delT  = 0;                                   % Temperature difference from nominal
g     = 1.26;                                % Ratio of specific heats
t0    = 6150*fToC + 273;                     % Combustion temperature
R     = 8.3/0.023;                           % Gas constant
l     = 72.4*inToM;                          % Engine length
m0    = (6515-513)*lbToKg;                   % Fuel mass
vol   = pi*rM^2*l;                           % Total engine volume
v0    = 0.076*vol;                           % Initial gas volume
tAve  = 17175*lbFToN;                        % Average thrust
pAve  = 605*psiToNm2;                        % Average pressure
aB    = 3905*inToM^2;                        % Average burning area
e     = 47.3;                                % Area ratio
pR    = inf;                                 % Pressure ratio
cF    = TCoeff(g,e,pR);                      % Thrust coefficient
aStar = tAve/(pAve*cF);                      % Throat area
cAB   = [aB  -aB];
nAB   = [0   120];

pEq   = ( (aB/aStar)*a*rhoP/sqrt((g/(R*t0))*(2/(g+1))^((g+1)/(g-1))) )^(1/(1-n));

Integrate

%-----------
x     = [1;v0;m0];
dT    = 0.1;
xPlot = zeros(length(x),1400);

for k = 1:size(xPlot,2)
  xPlot(:,k) = x;
  x          = x + dT*SolidR(g,t0,aStar,a,n,R,sigP,delT,rhoP,m0,cAB,nAB,rM,l,x);
end

Plot

%------
Plot2D(dT*(0:1399),[xPlot(1,:);xPlot(3,:);cF*aStar*xPlot(1,:)],'Time (sec)',...
                   ['Pressure '; 'Fuel Mass'; 'Thrust   '],'Solid Rocket')


%--------------------------------------

Published with MATLAB® R2019a