Attitude determination using a Kalman Filter

------------------------------------------------------------------------
See also KFSAAD, Delay, Quant, RaDec2U, DupVect, UE, ADGen
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 1994-1995 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

nsamples  = 600;

degToRad  = pi/180;
rPMToRPS  = 2*pi/60;

cant1     = 94*degToRad;
cant2     = 86*degToRad;
dihedral1 =  0*degToRad;
dihedral2 = 45*degToRad;

ssbias    = 0.0;
ssnoise   = 0.0*degToRad;
ssquant   = 0.000001*degToRad;

erbias    =  0.0;
cw1bias   =  0.0;
cw2bias   =  0.0;
da1bias   =  0.0;
da2bias   =  0.0;
cant1bias =  0.0;
cant2bias =  0.0;

Sun vector is constant in this demo

%------------------------------------
c10      = cos(10*degToRad);
s10      = sin(10*degToRad);
usun     = DupVect([c10;0;s10],nsamples);

qtype    = 'round';
onesigma = 0.0;
sunbias  = 0.0;
spinrate = 10*rPMToRPS;
quant    = 1.e-6;
delay    = 0;

The orbital elements

%---------------------
el(1)        = (42167 + 6800)/2;
el(2)        = 7 * pi/180;
el(3)        = 0;
el(4)        = 0;
el(5)        = 0.7;

The true attitude

%------------------
ra           =  1.5;
dec          = -0.4;
uspin        = RaDec2U(ra,dec);

Get the horizon sensor data and sun angles

%-------------------------------------------
cantAngle    = [cant1;cant2];
cantBias     = [cant1bias;cant2bias];
dihedralBias = [dihedral1;dihedral2];
mA           = linspace(pi/2,3*pi/2,nsamples);

[tLE,tTE,sa,unadir,eradius] = ADGen( el, usun, uspin, spinrate, mA, [delay;delay],...
                                     [quant;quant], [qtype;qtype], [onesigma;onesigma],...
                                     cantAngle, cantBias, dihedralBias, ssquant,...
                                     'round', ssnoise, ssbias, erbias );

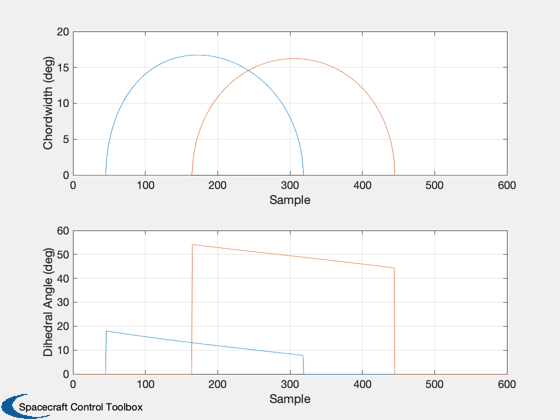
Reformat the data

%------------------
tte1 = tTE(1,:);
tte2 = tTE(2,:);
tle1 = tLE(1,:);
tle2 = tLE(2,:);

Extract the data with chordwidths above a threshold

%----------------------------------------------------
chordwidth1 = spinrate*(tte1-tle1);
chordwidth2 = spinrate*(tte2-tle2);

kr          = find(chordwidth1 > 6*degToRad | chordwidth2 > 6*degToRad);

us          =   usun(:,kr);
ue          = unadir(:,kr);
er          = eradius(kr);
cw1         = chordwidth1(kr) + cw1bias;
cw2         = chordwidth2(kr) + cw2bias;
da1         = 0.5*spinrate*(tte1(kr)+tle1(kr))-dihedral1 + da1bias;
da2         = 0.5*spinrate*(tte2(kr)+tle2(kr))-dihedral2 + da2bias;
sb          = sa(kr);

The state vector

%-----------------
%          1          2        3        4        5        6
% [       ra,       dec, cwbias1, cwbias2, dabias1, dabias2,
%          7          8        9      10
%  cantbias1, cantbias2, sunbias, erbias]

% Measurement functions
% Sun:            harc, dhdxarc
% Chordwidth:     hcw,  dhdxcw
% Dihedral angle: hda,  dhdxda

H    = zeros(1,10);

Initial guess

%--------------
x    = [1.5 -0.3  0.01 0 0  0 0 0  0 0]';
ff   = 0.1;
nits = 1;
Rsb  = 0.01;
Rcw  = 0.1;
Rda  = 0.1;
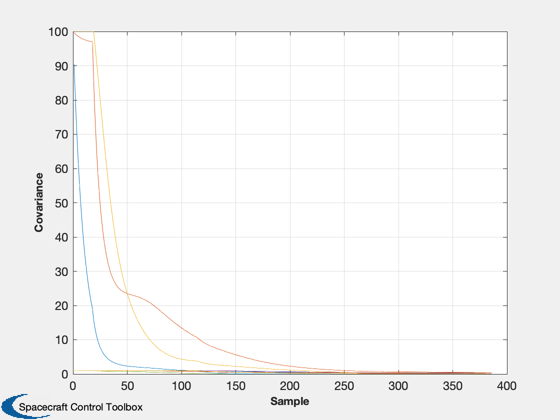
P    = diag([100,100,100,1,1,1,1,1,1,1]);

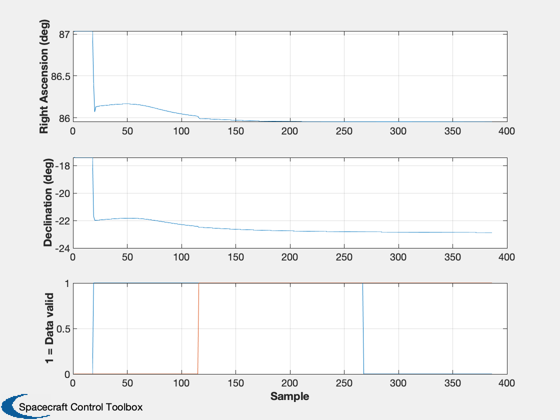
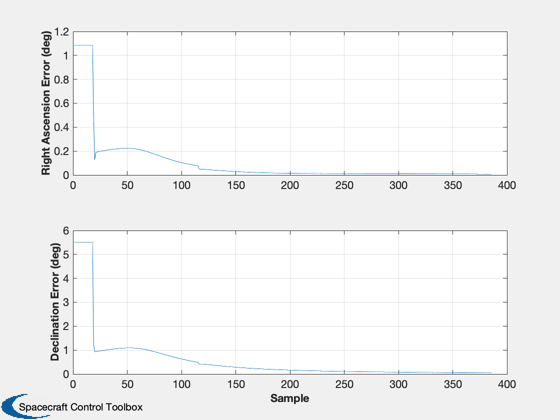
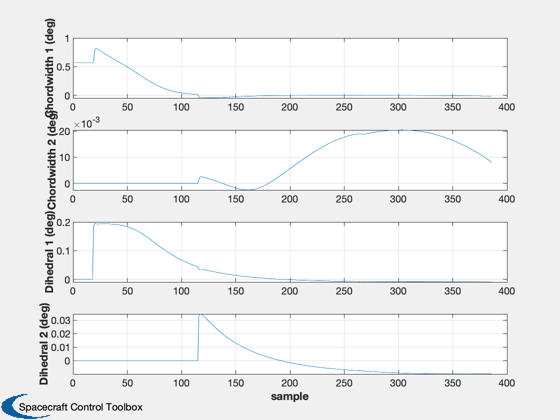
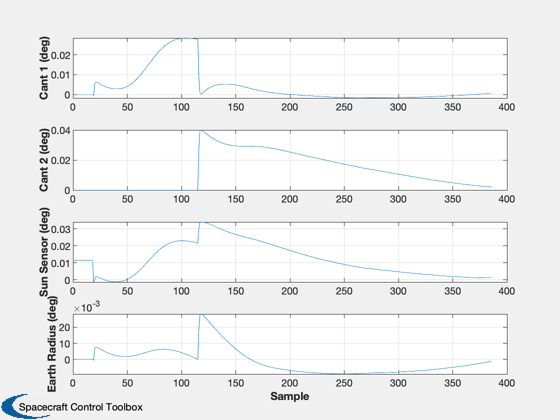
Call the Kalman filter. It will process all measurements and plot the results

%------------------------------------------------------------------------------
KFSAAD(x,P,Rcw,Rda,Rsb,cw1,cw2,da1,da2,sb,ue,us,er,cant1,cant2,ff,[],[ra,dec])


%--------------------------------------

Published with MATLAB® R2020a