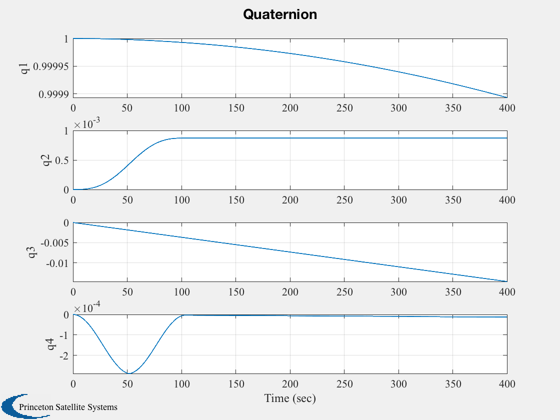
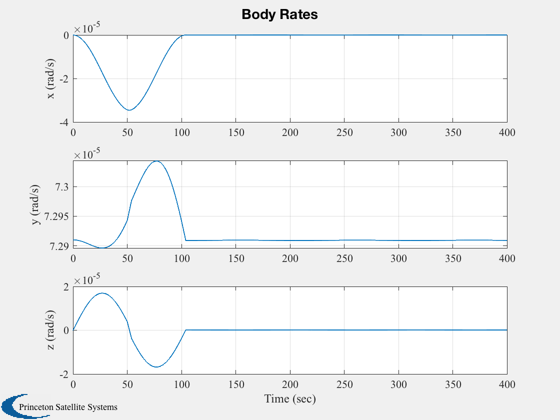
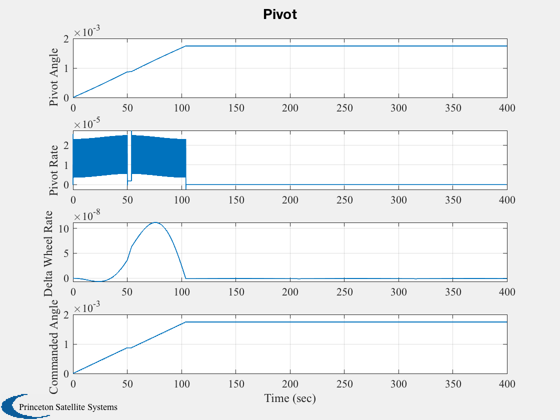
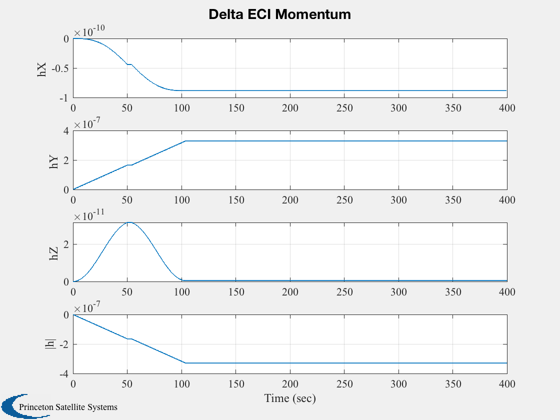
Simulates a pivot rotation.
The pivot is rotated in two steps. The steps are timed to be exactly one half nutation period apart. The results is that the spacecraft rolls and there is no nutation. The pivot stepping motor is modeled by a high bandwidth PD controller. The gains are selected by the fields:
d.pivotAngleGain d.pivotRateGain
The selected gains are the highest feasible with an integration time step of 0.0625 seconds.
The pivot is assumed to update every pivotUpdatePeriod.
------------------------------------------------------------------------ See also QTForm, Plot2D, TimeGUI, Jacobian, Mag, RK4, SCWithRollPivot ------------------------------------------------------------------------
Contents
%------------------------------------------------------------------------------- % Copyright (c) 1999 Princeton Satellite Systems, Inc. % All rights reserved. %-------------------------------------------------------------------------------
Global for the TimeGUI
%------------------------ global simulationAction simulationAction = ' ';
Spacecraft parameters
%---------------------- clear d; d.scInertia = diag([10000 2000 10000]); d.pivotInertia = eye(3); d.bWheelAlignment = [1 0 0;0 -1 0;0 0 -1]; d.wheelInertia = [1 0]; d.pivotAngleGain = 600; d.pivotRateGain = 2*.7071*sqrt(d.pivotAngleGain ); d.torque = [0;0;0]; d.torqueWheel = 0; d.commandedPivotAngle = 0; pivotPeriod = 50; pivotUpdatePeriod = 1/8; pivotRate = 0.002*pi/180;
Initialize the arrays
%----------------------
tEnd = 400;
dT = 0.0625;
nSim = tEnd/dT;
xPlot = zeros(15,nSim);
Initialize the time display
%---------------------------- [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, 0, [], 0, dT, 'Pivoted Wheel Simulation' );
Initial conditions
%-------------------
w = [0;7.291e-5;0];
wP = 0.0;
wW = 600;
x = [1;0;0;0; 0; w; wP; wW];
t = 0;
Find the half nutation period. I know it is element 7 because I looked!
%------------------------------------------------------------------------ a = Jacobian( 'SCWithRollPivot', x, 0, d ); s = eig(a); halfNutationPeriod = pi/imag(s(7));
Initial wheel rate and momentum
%-------------------------------- w0 = x(10); h0 = QTForm( x(1:4), SCWithRollPivot( x, t, d, 'h' ) ); magH0 = Mag(h0); tPivot = 0;
Simulate the pivot
%------------------- for k = 1:nSim % Display the status message %--------------------------- [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT ); % Angular momentum %----------------- h = QTForm( x(1:4), SCWithRollPivot( x, t, d, 'h' ) ); % Plots %------ xPlot(:,k) = [x;h - h0;Mag(h) - magH0;d.commandedPivotAngle]; % Propagate the state %--------------------- x = RK4( 'SCWithRollPivot', x, dT, t, d ); % The pivot control %------------------ if( t < pivotPeriod & t >= tPivot ) d.commandedPivotAngle = d.commandedPivotAngle + pivotRate*dT; tPivot = tPivot + pivotUpdatePeriod; elseif( t < pivotPeriod + halfNutationPeriod & t > halfNutationPeriod & t >= tPivot ) d.commandedPivotAngle = d.commandedPivotAngle + pivotRate*dT; tPivot = tPivot + pivotUpdatePeriod; elseif( t >= tPivot ) tPivot = tPivot + pivotUpdatePeriod; end % Update the time %---------------- t = t + dT; % Time control %------------- switch simulationAction case 'pause' pause simulationAction = ' '; case 'stop' return; case 'plot' break; end end
This is necessary if the simulation is terminated early
%---------------------------------------------------------- j = 1:k; t = (0:(k-1))*dT; xLbl = 'Time (sec)';
Plotting
%--------- xPlot(10,:) = xPlot(10,:) - w0; Plot2D( t, xPlot(1:4, j), xLbl, ['q1';'q2';'q3';'q4'], 'Quaternion' ); Plot2D( t, xPlot( 6: 8, j), xLbl, ['x (rad/s)';'y (rad/s)';'z (rad/s)'], 'Body Rates' ); yLbl = ['Pivot Angle ';... 'Pivot Rate ';... 'Delta Wheel Rate ';... 'Commanded Angle ']; Plot2D( t, xPlot([5 9 10 15],j), xLbl, yLbl, 'Pivot' ); Plot2D( t, xPlot(11:14, j), xLbl, ['hX ';'hY ';'hZ ';'|h|'], 'Delta ECI Momentum' ); %-------------------------------------- % PSS internal file version information %--------------------------------------