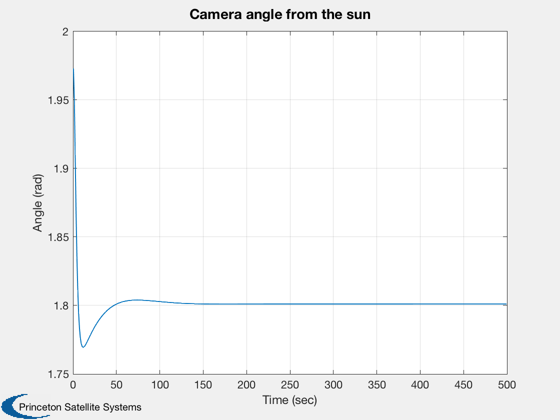
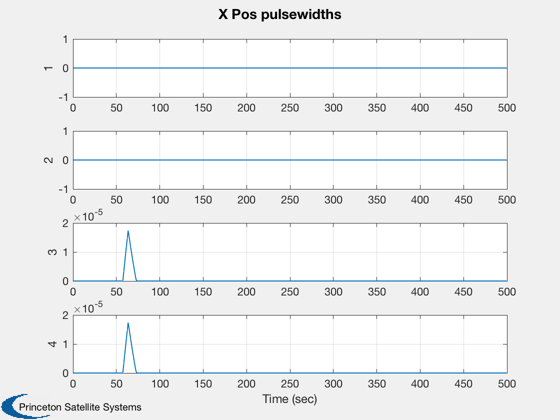
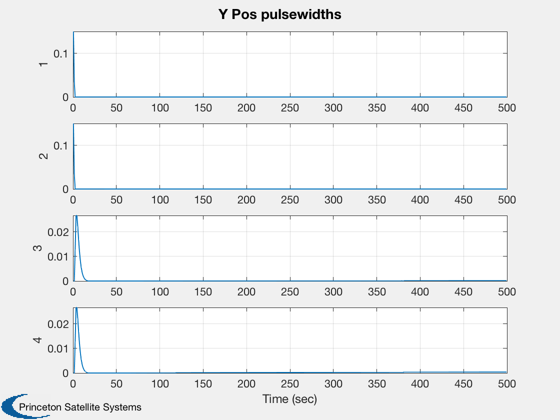
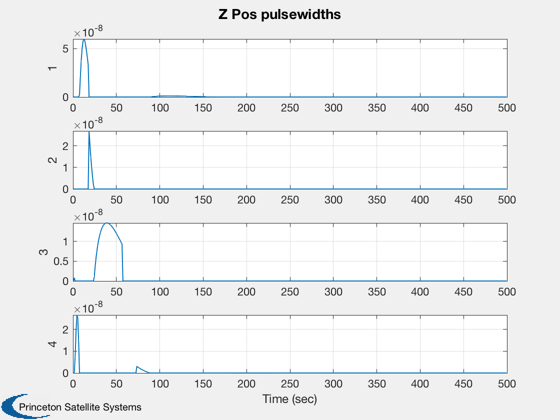
Implements a thruster control system. Uses a CAD model of the spacecraft.

------------------------------------------------------------------------
See also DeviceProperties, PIDMIMO, QMult, QPose, QTForm,
Constant, NPlot, Plot2D, TimeGUI, Cross, Dot, RK4, Simplex, JD2000, El2RV,
SunV1, Accel
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2003, 2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

Global for the TimeGUI

%------------------------
global simulationAction
simulationAction = ' ';

Constants

---------

degToRad = pi/180;
radToDeg = 180/pi;

Spacecraft model

----------------

g = load('SatWThrusters');

The control sampling period and the simulation integration time step

--------------------------------------------------------------------

tSamp       = 0.5;

Number of sim steps

-------------------

nSim        = 1000;

Plot every nPMax steps

----------------------

nP          = 0;
kP          = 0;
nPMax       = 2;
nPlot       = nSim/nPMax;

Print the time to go message every nTTGo steps

-----------------------------------------------

nTTGo       = 1000;

Spacecraft Inertias

-------------------

inr         = g.mass.inertia;
invInr      = inv(inr);
tDist       = [0;0;0]; % can add disturbances using this variable

% ------------------------------------------------------------------------------

Design the control loops with PIDMIMO

------------------------------------------------------------------------------

inr    = 1.0;  % unit inertia
zeta   = 1.0;  % damping ratio
omega  = 0.1;  % natural frequency
tauInt = 100;  % integrator time constant
wR     = 1.0;  % derivative term roll-off frequency
[a, b, c, d] = PIDMIMO( inr, zeta, omega, tauInt, wR, tSamp, 'Delta' ); % rEA_prop

Initialize the control system

-----------------------------

xRoll      = [0;0];
xPitch     = [0;0];
xYaw       = [0;0];
qTarget    = [0.99619;-0.087156;0;0];

Plotting arrays

---------------

x1Plot      = zeros( 7,nPlot);
x2Plot      = zeros( 6,nPlot);
aPlot       = zeros( 1,nPlot);
tPlot       = zeros( 1,nPlot);
pWPlot      = zeros(24,nPlot);

Initial conditions

------------------ q w

x1         = [[1;0;0;0];[0;0;0]];
el         = [Constant('earth radius mean')+500 45*pi/180 0 0 0 0];
[r,v]      = El2RV(el);
x2         = [r;v];

dTSim      = tSamp;
mET        = 0;
jD         = JD2000;
roll       = 0;
pitch      = 0;
yaw        = 0;

Get ideal force magnitude and direction for thrusters

%------------------------------------------------------
rEA_prop  = DeviceProperties('hydrazine thruster');
F         = zeros(3,24);
A         = zeros(3,24);
for k = 1:24
  rEA_prop(k) = g.component(k+2).deviceInfo;
  F(:,k) = rEA_prop(k).thrustCoefficient(1)*rEA_prop(k).unitVector;
  A(:,k) = Cross( rEA_prop(k).positionVector - g.mass.cM, F(:,k));
end

Initialize the time display

%----------------------------
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, [], 0, tSamp, 'REAControl' );

Run the simulation

------------------

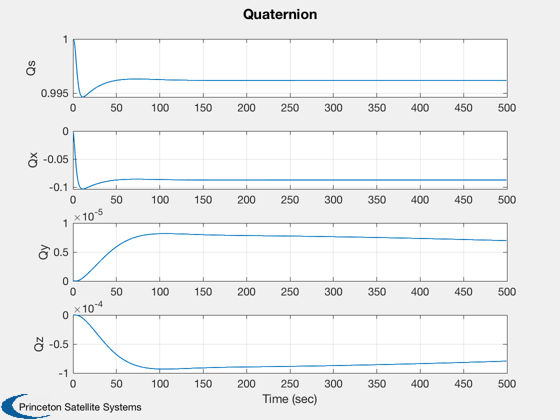
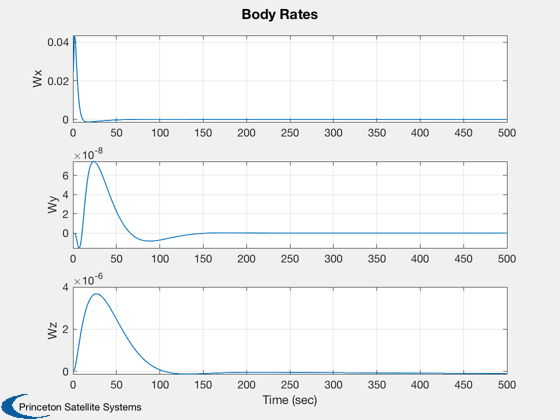
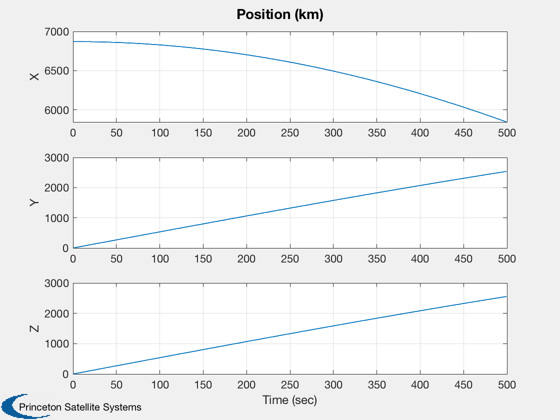
for k = 1:nSim

  % Display the status message
  %---------------------------
  [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, tSamp );

  % ------------------------------------------------------------------------------
  % Sensors
  % ------------------------------------------------------------------------------

  % Star Camera Angle
  % -----------------
  [uSun,rSun] = SunV1( jD, x2(1:3) );
  uCamera     = QTForm( x1(1:4), [0;0;1] );
  aCamera     = acos(Dot(uSun,uCamera));

  % ------------------------------------------------------------------------------
  % The Attitude Control System
  % ------------------------------------------------------------------------------

  % The attitude control loops
  % --------------------------
  % torque = AttitudeControlLaw( params );

  qTargetToBody = QPose( QMult( QPose(x1(1:4)), qTarget ) );

  % Small angle convention
  %-----------------------
  angleError = -2*qTargetToBody(2:4);

  % Controller blocks, delta format. Each axis uses the same gains.
  %----------------------------------------------------------------
  accel    = zeros(3,1);
  accel(1) =          c*xRoll  + d*angleError(1);
  xRoll    = xRoll  + a*xRoll  + b*angleError(1);

  accel(2) =          c*xPitch + d*angleError(2);
  xPitch   = xPitch + a*xPitch + b*angleError(2);

  accel(3) =         c*xYaw   + d*angleError(3);
  xYaw     = xYaw  + a*xYaw   + b*angleError(3);

  torque = -g.mass.inertia*accel;

  % Distribute torque command to thrusters
  % --------------------------------------------------------
  pulsewidthDemand = Simplex( ones(1,24), A, torque, 1 );
  demandError      = norm( A*pulsewidthDemand - torque );
  pulsewidthDemand = tSamp*pulsewidthDemand;

  % Ideal thruster model - apply pulsewidths exactly as calculated
  %---------------------------------------------------------------
  force = F*pulsewidthDemand;

  % -------------------------------------------------------------------------------
  % Disturbances
  % -------------------------------------------------------------------------------
  % Add simple periodic disturbance
  tDist = [1;0;0.5]*1e-3*sin(0.0011*mET);
  fDist = [0;0;0];

  % -------------------------------------------------------------------------------
  % Update the equations of motion
  % -------------------------------------------------------------------------------
  x1       = RK4('FRB',x1,dTSim,mET,inr,invInr,torque+tDist);
  x2       = RK4('FOrbCart',x2,dTSim,jD,(force+fDist)/g.mass.mass);
  mET      = mET + dTSim;
  jD       = jD + dTSim/86400;

  % Plotting
  % --------
  if( nP == 0 )
    kP           = kP + 1;
    x1Plot(:,kP) = x1;
  	x2Plot(:,kP) = x2;
  	aPlot(:,kP)  = aCamera;
  	pWPlot(:,kP) = pulsewidthDemand;
    tPlot(:,kP)  = mET;
    nP           = nPMax - 1;
  else
    nP           = nP - 1;
  end

  % Time control
  %-------------
  switch simulationAction
    case 'pause'
      pause
      simulationAction = ' ';
    case 'stop'
      return;
    case 'plot'
      break;
  end

end

j = 1:kP;

tPlot = tPlot(j);

Plot2D(tPlot,x1Plot( 1: 4,j),'Time (sec)',['Qs';'Qx';'Qy';'Qz'],'Quaternion')
Plot2D(tPlot,x1Plot( 5: 7,j),'Time (sec)',['Wx';'Wy';'Wz'],'Body Rates')
Plot2D(tPlot,x2Plot( 1:3,j),'Time (sec)',['X';'Y';'Z'],'Position (km)')
Plot2D(tPlot,aPlot(:,j),'Time (sec)',['Angle (rad)'],'Camera angle from the sun')
Plot2D(tPlot,pWPlot(1:4,j),'Time (sec)',['1';'2';'3';'4'],'X Pos pulsewidths')
Plot2D(tPlot,pWPlot(5:8,j),'Time (sec)',['1';'2';'3';'4'],'Y Pos pulsewidths')
Plot2D(tPlot,pWPlot(9:12,j),'Time (sec)',['1';'2';'3';'4'],'Z Pos pulsewidths')
Plot2D(tPlot,pWPlot(13:16,j),'Time (sec)',['1';'2';'3';'4'],'X Neg pulsewidths')
Plot2D(tPlot,pWPlot(17:20,j),'Time (sec)',['1';'2';'3';'4'],'Y Neg pulsewidths')
Plot2D(tPlot,pWPlot(21:24,j),'Time (sec)',['1';'2';'3';'4'],'Z Neg pulsewidths')

%--------------------------------------

Published with MATLAB® R2019a