This script explores different roll/yaw controllers.
The plant model is obtained from RYDyn.
The controllers are SISO, linear quadratic regulator and estimator, and
quadratic controller. The open and closed loop response to a periodic
disturbance are plotted.
------------------------------------------------------------------------
See also @statespace/statespace.m, C2DZOH, DQCE, DQCR, LQC, Constant,
Plot2D, RYDyn, Geo
------------------------------------------------------------------------
Contents
Constants
clear w;
degToRad = Constant('deg to rad');
radToDeg = Constant('rad to deg');
secInDay = 86400;
wo = Geo;
hW = 60;
iAxis = [1 3];
inr = diag([1000 200 1000]);
hMWA = [0;-1;0]*hW;
wO = [0;-1;0]*wo;
Plant models
[aP, bP, cP, dP, aL, bL, cL, dL, wP] = RYDyn( inr, hMWA, wO, iAxis);
a = aL;
b = bL;
c = [1 0];
d = [0 0];
For simulations
t = linspace(0,4*secInDay,1000);
dT = t(2);
days = t/secInDay;
Body fixed torque and inertially fixed torque
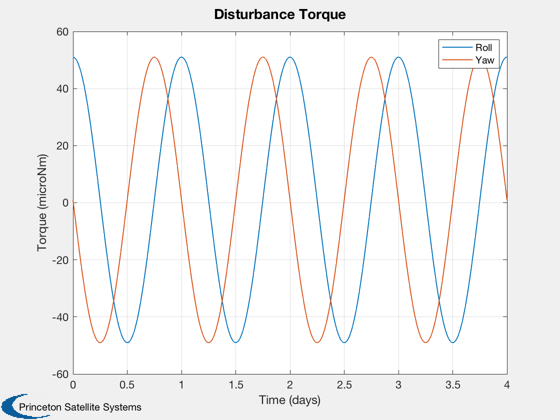
uD = 1e-6*[1 + 50*cos(t*2*pi/secInDay);1 - 50*sin(t*2*pi/secInDay)];
Plot2D(days,1e6*uD ,'Time (days)','Torque (microNm)', 'Disturbance Torque')
legend('Roll','Yaw')
Open loop plant
[aD, bD] = C2DZOH( a, b, dT );
x = zeros(2,length(t));
for k = 2:length(t)
x(:,k) = aD*x(:,k-1) + bD*uD(:,k-1);
end
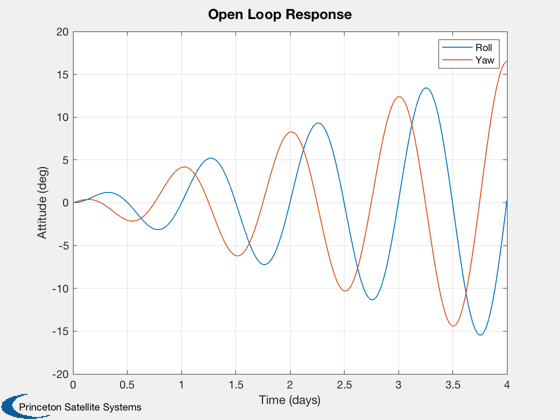
Plot2D(days,x*radToDeg ,'Time (days)','Attitude (deg)','Open Loop Response')
legend('Roll','Yaw')
SISO controller
wN = 5*wo;
zeta = 0.7071;
disp('Classical Gain Matrix')
kRY = -[(wo^2-wN^2)/wo;2*zeta*wN]*hW
Classical Gain Matrix
kRY =
0.105006468316193
-0.030937530727658
Closed loop simulation
x = zeros(2,length(t));
u = zeros(2,length(t));
for k = 2:length(t)
y = x(1,k-1);
u(:,k) = -kRY*y;
x(:,k) = aD*x(:,k-1) + bD*(uD(:,k-1) + u(:,k));
end
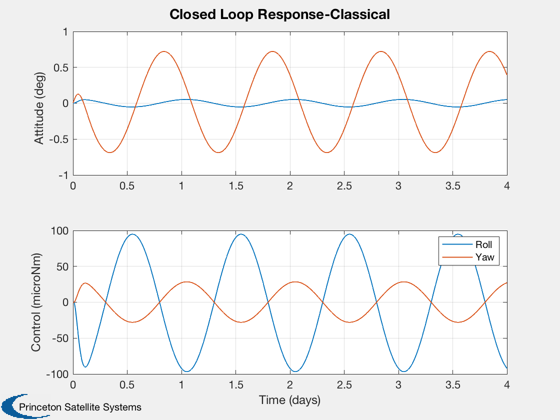
Plot2D(days,[x*radToDeg;u/1e-6] ,'Time (days)',['Attitude (deg) ';'Control (microNm)'],...
'Closed Loop Response-Classical',[],['[1,2]';'[3,4]'])
legend('Roll','Yaw')
Linear quadratic regulator and estimator
h = [1 0];
qE = 100*eye(2);
rE = 1;
qC = eye(2);
rC = eye(2);
kE = DQCE( aD, bD, h, qE, rE );
disp('QCR/QCE Gain Matrix')
kC = DQCR( aD, bD, eye(2), eye(2) )
x = zeros(2,length(t));
xE = zeros(2,length(t));
u = zeros(2,length(t));
for k = 2:length(t)
y = h*x(:,k-1);
u(:,k) = -kC*xE(:,k-1);
xE(:,k) = aD*xE(:,k-1) + bD*u(:,k) + kE*(y - [1 0]*xE(:,k-1));
x(:,k) = aD*x(:,k-1) + bD*(uD(:,k-1) + u(:,k));
end
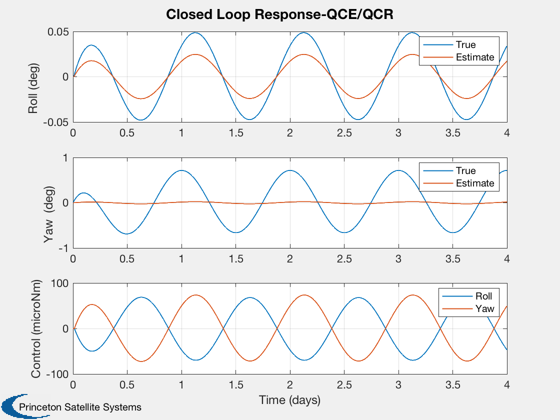
[h, hA] = Plot2D(days,[x*radToDeg;xE*radToDeg;u/1e-6] ,'Time (days)',['Roll (deg) ';...
'Yaw (deg) ';'Control (microNm)'], 'Closed Loop Response-QCE/QCR',[],['[1,3]';'[2,4]';'[5,6]']);
legend(hA(1).h,'True','Estimate')
legend(hA(2).h,'True','Estimate')
legend(hA(3).h,'Roll','Yaw')
QCR/QCE Gain Matrix
kC =
-0.002125510563329 0.168503305647950
-0.168503305647952 -0.002125510563328
Output feedback
g = statespace( a, b, c, d, 'Roll/Yaw',['Roll','Yaw '],['Roll','Yaw '],'Roll');
Control Weights
w.r = rC;
State Weighting
w.q = qC;
w.k = kRY;
Generate the output feedback controller
[gC, j] = LQC( g, w, 'lqof' );
fprintf('Output Feedback cost reduction from %12.4e to %12.4e\n\n',j.initial,j.final)
disp('Output Feedback Gain Matrix')
kC = get( gC, 'd' )
Output Feedback cost reduction from 1.4086e+04 to 6.9167e+03
Output Feedback Gain Matrix
kC =
0.995634244861754
-1.004346662639282
The output feedback system is much higher gain and needs a smaller dT
t = linspace(0,4*secInDay,4000);
uD = 1e-6*[1 + 50*cos(t*2*pi/secInDay);1 - 50*sin(t*2*pi/secInDay)];
dT = t(2);
[aD,bD] = C2DZOH(a,b,dT);
x = zeros(2,length(t));
u = zeros(2,length(t));
for k = 2:length(t)
y = x(1,k-1);
u(:,k) = -kC*y;
x(:,k) = aD*x(:,k-1) + bD*(uD(:,k-1) + u(:,k));
end
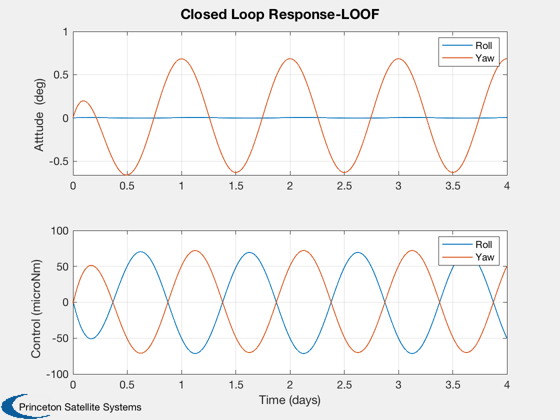
[h, hA] = Plot2D(t/secInDay,[x*radToDeg;u/1e-6] ,'Time (days)',['Atttude (deg) ';'Control (microNm) '],...
'Closed Loop Response-LOOF',[],['[1,2]';'[3,4]']);
legend(hA(1).h,'Roll','Yaw')
legend(hA(2).h,'Roll','Yaw')