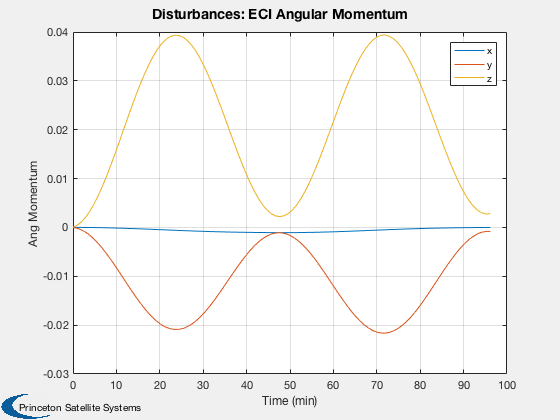
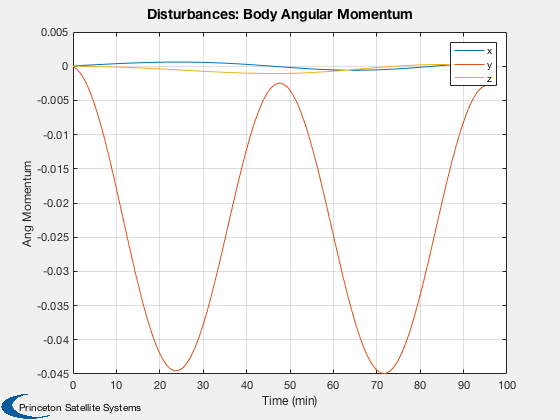
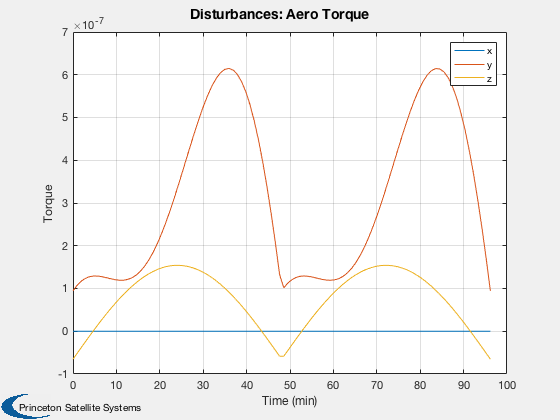
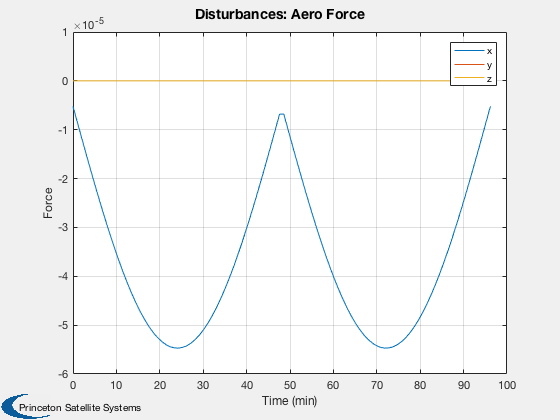
Run the disturbance model for a spacecraft with two rotating arrays.

Define the orbit a priori and call the disturbance model in batch. The sun vector is held constant. The spacecraft - body 1 - points at the sun while the arrays - bodies 2 and 3 - rotate to point at the sun.

Before the disturbances are calculated, the orientation is visualized in a loop using DrawSCPlanPlugIn. ------------------------------------------------------------------------ See also Disturbances, BuildTwoArraySC, Q2Mat, QLVLH, Date2JD, Period, RVFromKepler, SunV1 ------------------------------------------------------------------------

Load the CAD model of the demo spacecraft
Ephemeris
Disturbances
Initialize the disturbance model
Do 100 samples in a circular orbit
A circular orbit with LVLH pointing
Run

%-------------------------------------------------------------------------------
%  	Copyright (c) 1998-2003 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------
%   Since version 5.5 (2003)
%   2016.1 Add visualization of Earth and Sun vectors with DrawSCPlanPlugIn to
%   verify correct solar panel pointing
%-------------------------------------------------------------------------------

Load the CAD model of the demo spacecraft

%-----------------------
g = load('TwoArraySC')

g = 
  struct with fields:

         body: [1×3 struct]
    component: [1×34 struct]
         mass: [1×1 struct]
         name: 'Demo Spacecraft'
        omega: [3×1 double]
            q: [4×1 double]
        qLVLH: [4×1 double]
         rECI: [3×1 double]
       radius: 3.735
    subsystem: [1×6 struct]
        units: 'mks'
         vECI: [3×1 double]

Ephemeris

%----------
jD           = Date2JD([3 22 2001 0 0 0]); % Equinox
[uSun, rSun] = SunV1( jD );

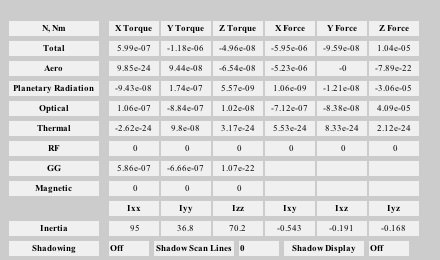
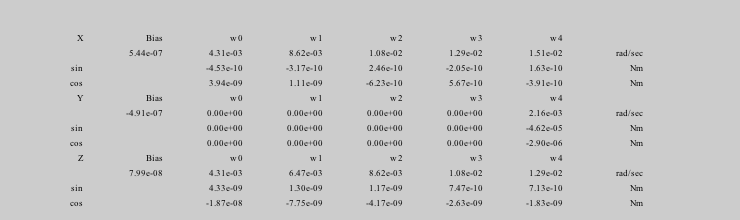
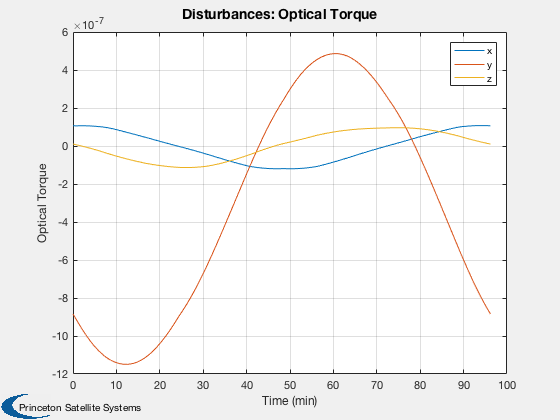
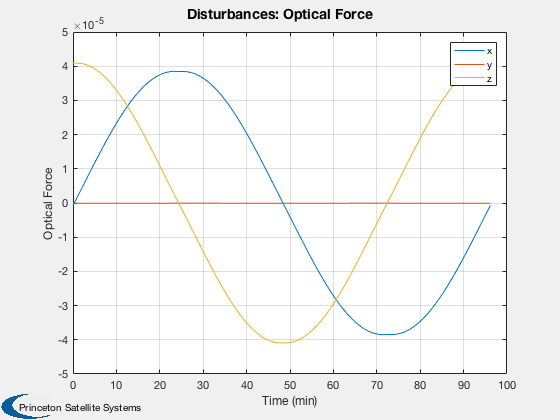
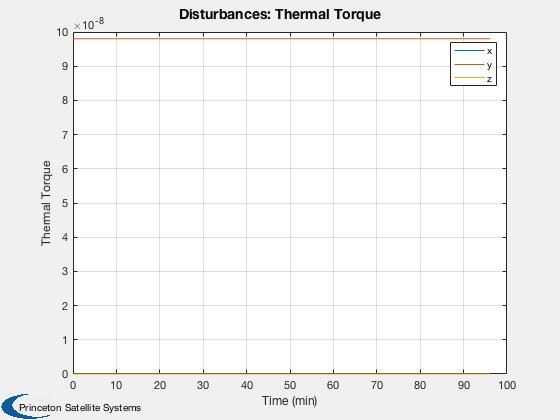
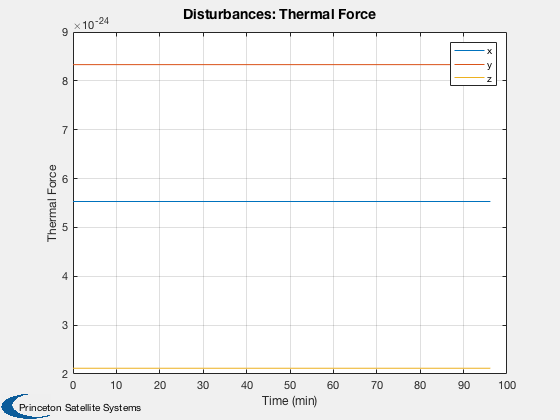
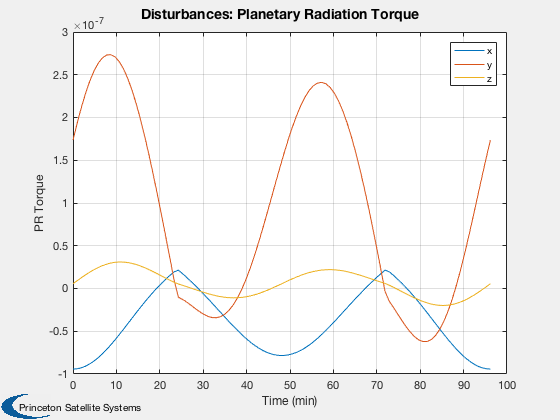
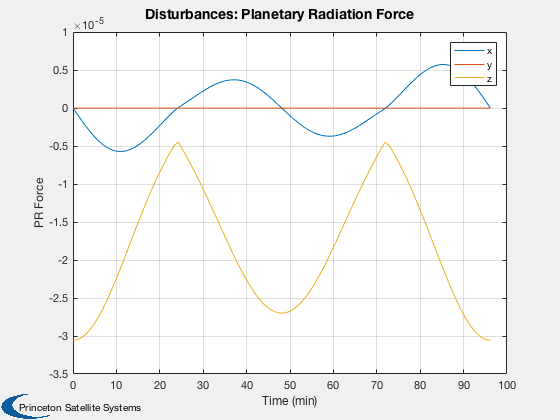
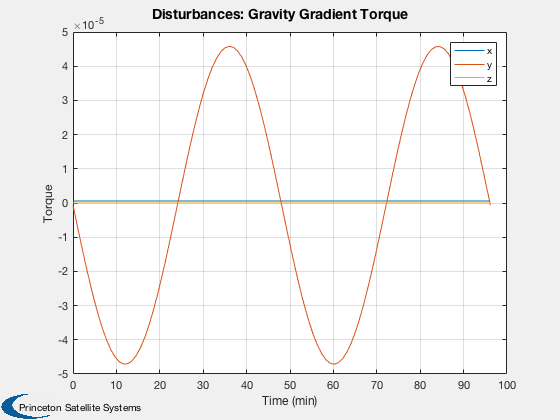
Disturbances

%-------------
d           = Disturbances('defaults');
solarFlux   = 1367; % Watts/m^2
d.s         = solarFlux*uSun;
d.shadow    = false;
d.units     = 'm';
d.planet    = 'earth';

Initialize the disturbance model

%---------------------------------
hD          = Disturbances( 'init', g, d );

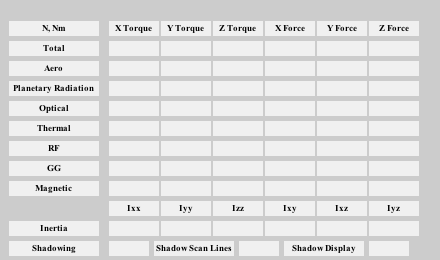
Do 100 samples in a circular orbit

%----------------------------------
nSamp       = 100;
rOrbit      = 7000;
period      = Period(rOrbit);
d.tSamp     = period/nSamp;
theta       = linspace(0,2*pi,nSamp);
c           = cos(theta);
s           = sin(theta);

A circular orbit with LVLH pointing

%-------------------------------------
[d.r,d.v]   = RVFromKepler([rOrbit 0.5 0 0 0 0],linspace(0,period,nSamp));
qLVLH       = QLVLH( d.r, d.v );

% Create the transformation matrix arrays.
% In this case we are using angles and
% axes. Visualize the result.
%----------------------------------------
gD = g;
gD.subsystem = [];
for k = 1:nSamp
  g.body(1).bHinge(k).b     = Q2Mat( qLVLH(:,k) )';
  g.body(2).bHinge(k).angle = theta(k);
  g.body(2).bHinge(k).axis  = 2;
  g.body(3).bHinge(k).angle = theta(k);
  g.body(3).bHinge(k).axis  = 2;

  % Display
  gD.body(1).bHinge = g.body(1).bHinge(k);
  gD.body(2).bHinge = g.body(2).bHinge(k);
  gD.body(3).bHinge = g.body(3).bHinge(k);
  gD.rECI = d.r(:,k);
  gD.vECI = d.v(:,k);
  if k == 1
    tag = DrawSCPlanPlugIn(gD);
    view(45,25)
  end
  DrawSCPlanPlugIn( 'vectors', tag, gD, uSun );
  drawnow;
end

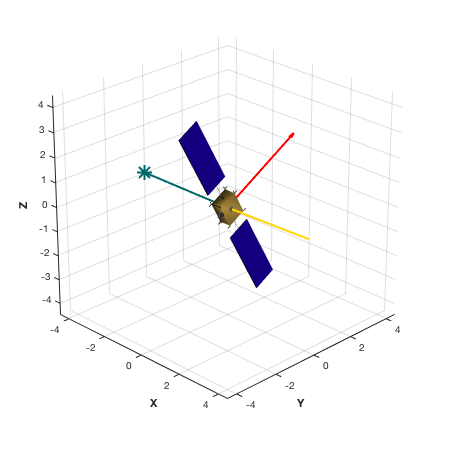
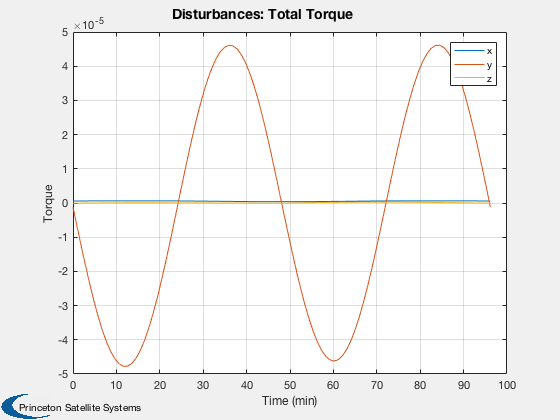
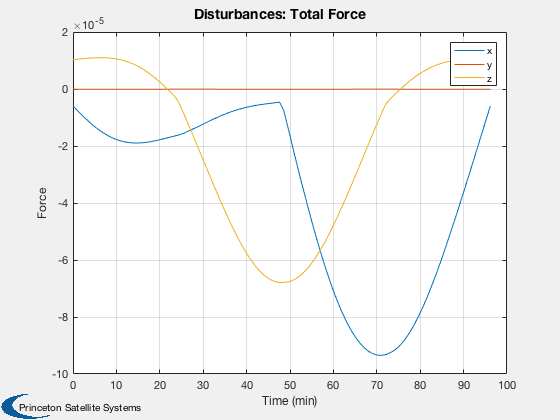
Run

%-----
Disturbances( 'run', g, d, hD );
Figui;


%--------------------------------------
% PSS internal file version information
%--------------------------------------