Example 4.2 and 4.3 in the reference.

We are using RK4 for this example but would use RK45 in practice since it has error checking.

------------------------------------------------------------------------- See also NewFig, XLabelS, YLabelS, RK4 -------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 1996 Princeton Satellite Systems.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2.
%--------------------------------------------------------------------------

fprintf('Pendulum with Sliding Mass\n--------------------------\n\n')

nSim = 400;
dT   = 0.001;

Pendulum with Sliding Mass
--------------------------

System properties

%-------------------
m1 = 1;
m2 = 2;
L  = 4;
g  = 9.806;

Solve in independent coordinates

%----------------------------------
q = [2; pi/4; 0; 0];

xIPlot = zeros(4,nSim);
tic
for k = 1:nSim
  q           = RK4( 'FIC', q, dT, 0, m1, m2, L, g );
  xIPlot(:,k) = [q(1)*cos(q(2));...
                 q(1)*sin(q(2));...
		            L*cos(q(2));...
			        L*sin(q(2))];
end
tI = toc;
fprintf('Time for the independent coordinate method %8.3f sec\n',tI);

Time for the independent coordinate method    0.061 sec

Solve in dependent coordinates

%--------------------------------
x         = [2;2;4;4;0;0;0;0]*cos(pi/4);
alpha     = 1e7;
mu        = 0.7071;
omega     = 1.0;
dynData   = [m1 m2 g];
constData = L^2;
penalty   = [alpha 2*mu*omega omega^2];

xDPlot = zeros(4,nSim);
nIts = 5;
tic
for k = 1:nSim
  x           = RK4( 'FDC', x, dT, 0, 'Dyn', 'KConst', dynData, constData, penalty, nIts );
  xDPlot(:,k) = x(1:4);
end
tD = toc;
fprintf('Time for the Lagrange Multiplier method    %8.3f sec\n',tD);
fprintf('The Lagrange method with %i iterations takes  %3.0f%% longer\n',nIts, 100*(tD/tI - 1));

Time for the Lagrange Multiplier method       0.207 sec
The Lagrange method with 5 iterations takes  240% longer

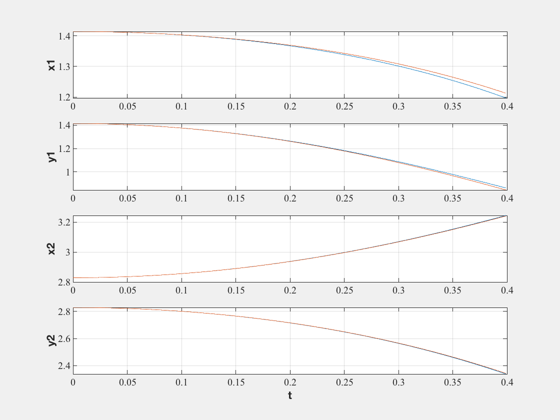
Plot the results

%------------------
t = dT*(0:(nSim-1));

NewFig('Independent Coordinates')
subplot(4,1,1)
plot(t,xIPlot(1,:),t,xDPlot(1,:))
YLabelS('x1')
grid
subplot(4,1,2)
plot(t,xIPlot(2,:),t,xDPlot(2,:))
YLabelS('y1')
grid

subplot(4,1,3)
plot(t,xIPlot(3,:),t,xDPlot(3,:))
YLabelS('x2')
grid
subplot(4,1,4)
plot(t,xIPlot(4,:),t,xDPlot(4,:))
YLabelS('y2')
XLabelS('t')
grid

%---------------------------------------------------------------------------------------------------

Single pendulum

%---------------------------------------------------------------------------------------------------
fprintf('\nSingle Pendulum\n---------------\n\n')

nSim = 1000;

Single Pendulum
---------------

System properties

%-------------------
m  = 1;
L  = 2;
g  = 9.806;

Solve in independent coordinates

%----------------------------------
q = [pi/8; 0];

xIPlot = zeros(2,nSim);
tic
for k = 1:nSim
  q           = RK4( 'FICP', q, dT, 0, L, g );
  xIPlot(:,k) = -L*[ sin(q(1));...
                     cos(q(1))];
end
tI = toc;
fprintf('Time for the independent coordinate method %8.3f sec\n',tI);

Time for the independent coordinate method    0.068 sec

Solve in dependent coordinates

%--------------------------------
x         = -L*[sin(pi/8);cos(pi/8);0;0];
alpha     = 1e7;
mu        = 0.7071;
omega     = 1.0;
dynData   = [m g];
constData = L^2;
penalty   = [alpha 2*mu*omega omega^2];

xDPlot = zeros(2,nSim);
nIts = 5;
tic
for k = 1:nSim
  x           = RK4( 'FDC', x, dT, 0, 'DynP', 'KConstP', dynData, constData, penalty, nIts );
  xDPlot(:,k) = x(1:2);
end
tD = toc;
fprintf('Time for the Lagrange Multiplier method    %8.3f sec\n',tD);
fprintf('The Lagrange method with %i iterations takes  %3.0f%% longer\n',nIts, 100*(tD/tI - 1));

Time for the Lagrange Multiplier method       0.522 sec
The Lagrange method with 5 iterations takes  664% longer

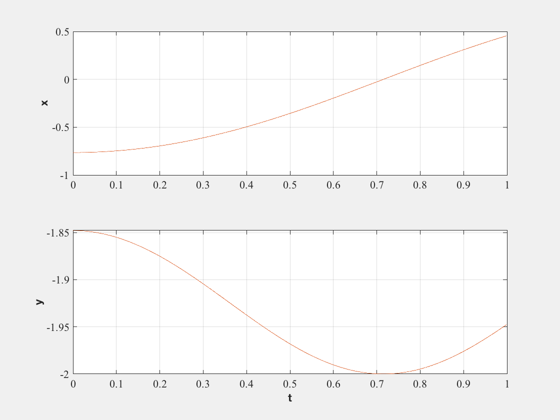
Plot the results

%------------------
t = dT*(0:(nSim-1));
NewFig('Independent Coordinates')
subplot(2,1,1)
plot(t,xIPlot(1,:),t,xDPlot(1,:))
YLabelS('x')
grid
subplot(2,1,2)
plot(t,xIPlot(2,:),t,xDPlot(2,:))
YLabelS('y')
grid
XLabelS('t')


%---------------------------------------------------------------------------------------------------

Slider Crank

%---------------------------------------------------------------------------------------------------
fprintf('\nSlider Crank\n------------\n\n')

nSim = 1000;

Slider Crank
------------

System properties

%-------------------
m  = 1;
L  = 2;
g  = 9.806;

Solve in dependent coordinates

%--------------------------------
x         = -L*[sin(pi/8);cos(pi/8);0;0];
alpha     = 1e7;
mu        = 0.7071;
omega     = 1.0;
dynData   = [m g];
constData = L^2;
penalty   = [alpha 2*mu*omega omega^2];

xDPlot = zeros(2,nSim);
nIts = 5;
tic
for k = 1:nSim
  x           = RK4( 'FDC', x, dT, 0, 'DynP', 'KConstP', dynData, constData, penalty, nIts );
  xDPlot(:,k) = x(1:2);
end
tD = toc;
fprintf('Time for the Lagrange Multiplier method    %8.3f sec\n',tD);
fprintf('The Lagrange method with %i iterations takes  %3.0f%% longer\n',nIts, 100*(tD/tI - 1));

Time for the Lagrange Multiplier method       0.306 sec
The Lagrange method with 5 iterations takes  348% longer

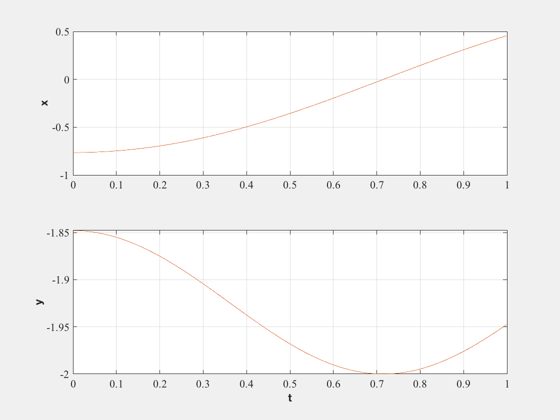
Plot the results

%------------------
t = dT*(0:(nSim-1));
NewFig('Independent Coordinates')
subplot(2,1,1)
plot(t,xIPlot(1,:),t,xDPlot(1,:))
YLabelS('x')
grid
subplot(2,1,2)
plot(t,xIPlot(2,:),t,xDPlot(2,:))
YLabelS('y')
grid
XLabelS('t')


%--------------------------------------

Published with MATLAB® R2019a