Demonstrate two body dynamics using the two body dynamics model.

See TBModel and FTB.

------------------------------------------------------------------------
See also QTForm, NPlot, Plot2D, RK4, TBModel
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 1995, 2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 1.
%--------------------------------------------------------------------------


%   r0             (3,1)     The vector from the origin to the body 0 cm in the body 0 frame
%   r1             (3,1)     The vector from the origin to the hinge in the body 0 frame
%   lam1           (3,1)     The vector from the hinge to the body 1 cm in the body 1 frame
%   iner0          (3,3)     The body 0 inertia in the body 0 frame
%   iner1          (3,3)     The body 1 inertia in the body 1 frame
%   m0                       The body 0 mass
%   m1                       The body 1 mass

r0    = [1;1;1];
r1    = [1;1;1];
lam1  = [1;1;1];
iner0 = 1000*[1.0, 0.1, 0.1; 0.1, 2.0, 0.1; 0.1, 0.1, 3.0];
iner1 =  100*[1.0, 0.1, 0.1; 0.1, 2.0, 0.1; 0.1, 0.1, 3.0];
m0    = 1000;
m1    =    1;

Initial State

%--------------

dOF     = 1;
nDOF    = length(dOF);
nStates = 11+length(dOF);

q       = [1;0;0;0];
q0To1   = [1;0;0;0];
w0      = [0.01;0.01;0.01];
w1      = 0.01*ones(nDOF,1);
tExt    = [0;0;0];
tInt    = 1.e-5*ones(nDOF,1);
torque  = [tExt;tInt];
force   = zeros(6,1);

x       = [q;q0To1;w0;w1];
dTSim   = 0.5;

nSim  = 100;
nPMax = 10;
nPlot = nSim/nPMax;
xPlot = zeros(nStates,nPlot);
tPlot = zeros(      1,nPlot);
hPlot = zeros(      4,nPlot);

%-------------------

Run the simulation

%-------------------

kP     = 0;
nP     = 0;
t      = 0;

for k = 1:nSim

  % Angular Momentum
  %-----------------
  q0To1 = x(5:8);
  w0    = x(9:11);
  w1    = x(12:nStates);

  [wdot,h,iner] = TBModel( w0, w1, q0To1, r0, r1, lam1, iner0, iner1, m0, m1, torque, force, dOF );

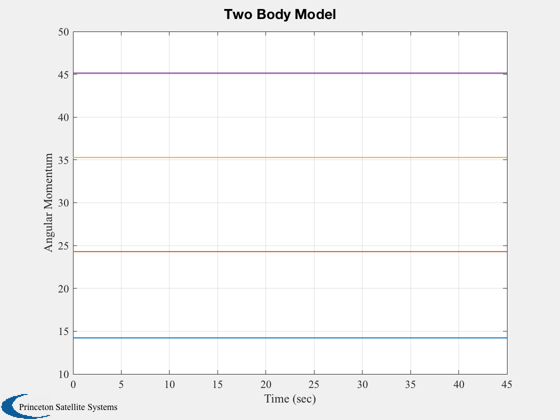
  hECI  = QTForm( x(1:4), h );

  % Plotting
  %---------
  if( nP == 0 )
    kP                  = kP + 1;
    xPlot(:,kP)         = x;
    hPlot(:,kP)         = [hECI;sqrt(h'*h)];
    tPlot(kP)           = t;
    nP                  = nPMax - 1;
  else
    nP                  = nP - 1;
  end

  % --------------
  % The simulation
  % --------------

  x = RK4( @FTB, x, dTSim, t, r0, r1, lam1, iner0, iner1, m0, m1, torque, force, dOF );
  t = t + dTSim;

end

Plot2D(tPlot,hPlot,'Time (sec)','Angular Momentum','Two Body Model')
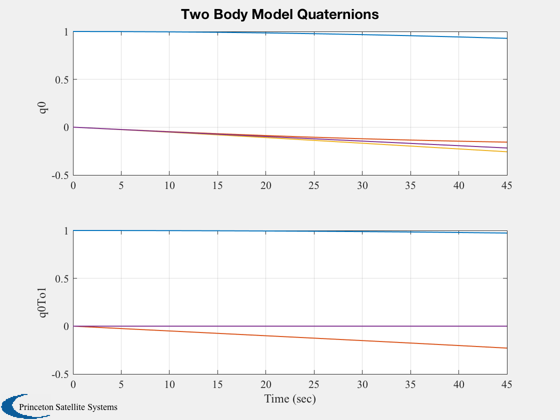
Plot2D(tPlot,xPlot(1:8,:),'Time (sec)',{'q0','q0To1'},'Two Body Model Quaternions','lin',...
  {'[1:4]','[5:8]'})
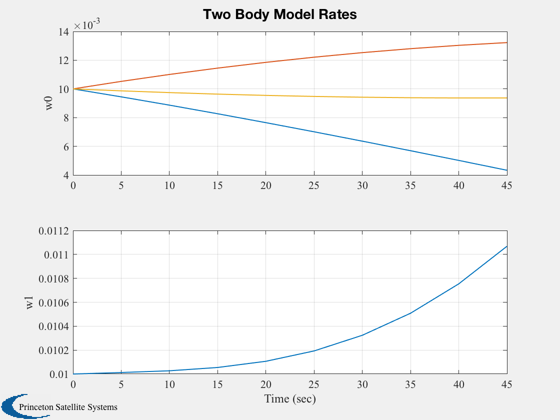
Plot2D(tPlot,xPlot(9:end,:),'Time (sec)',{'w0','w1'},'Two Body Model Rates','lin',...
  {'[1:3]','[4]'})


%--------------------------------------

Published with MATLAB® R2019a