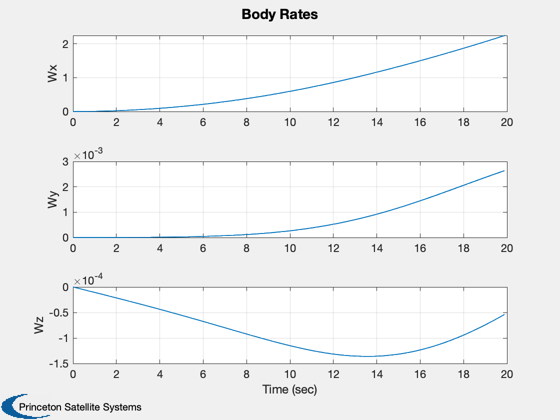
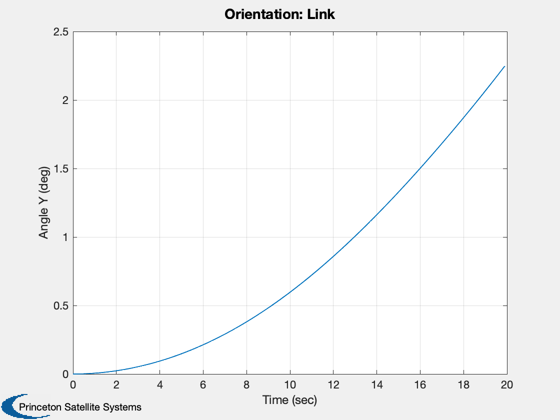
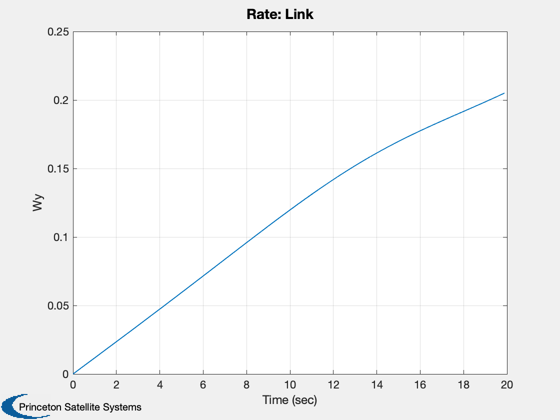
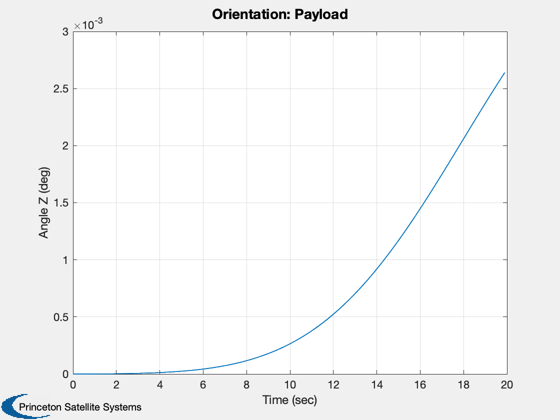
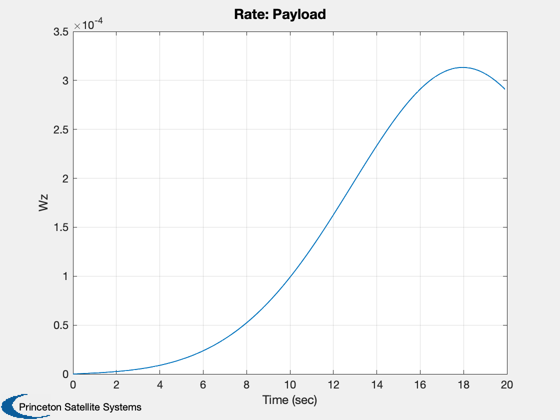
Three body simulation. The bodies are connected

1 - y DOF - 2 - zDOF - 3

Overall there are 5 dof.

See TreeCAD.m for a demonstration of how to use Tree with the CAD
functions.

Since version 2.
------------------------------------------------------------------------
See also TimeGUI, Mag, RK4, TreeAdd, TreeH, TreeInit, TreePlot, TreePrnt
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright 1997-1998 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

Global for the time GUI

%------------------------
global simulationAction
simulationAction = ' ';
clear body;

Vectors from previous body reference to the hinge of the body

%--------------------------------------------------------------
lambda1 = [0;0;0];
lambda2 = [2;0;0];
lambda3 = [1;0;0];

% Vector from body reference to body c.m. For all but the core

the reference is always the hinge that leads to the core

%-------------------------------------------------------------
r1      = [0;0;0];
r2      = [0;0.5;0];
r3      = [0;0;0.5];

Mass and inertia

%-----------------
m1      = 100;
m2      = 2;
m3      = 5;
i1      = diag([200 200 300]);
i2      = diag([  1   1   1]);
i3      = diag([  3   3   1]);

Add each body to the tree data structure

%-----------------------------------------
body(1) = TreeAdd( i1, r1, lambda1, m1, 0, 0, [], [], [], [], [], 'Core' );
body(2) = TreeAdd( i2, r2, lambda2, m2, 1, 2, [], [], [], [], [], 'Link' );
body(3) = TreeAdd( i3, r3, lambda3, m3, 2, 3, [], [], [], [], [], 'Payload' );

Internal torque

%----------------
body(2).torque = 0.1;

Initial orbit

%--------------
r = [7000;0;0];
v = [0;sqrt(3.98600436e5/7000);0];

Initialize the multibody tree

%------------------------------
[treeDS, x]  = TreeInit( body, r, v );

Print out the tree

%-------------------
TreePrnt( body, treeDS );

-----------------------------------------------------------------------
Body 1: Core
-----------------------------------------------------------------------
Inertia                =     200.0000       0.0000       0.0000
                               0.0000     200.0000       0.0000
                               0.0000       0.0000     300.0000

Mass                   =     100.0000

CM Location            =       0.0000       0.0000       0.0000

Vector to Hinge        =       0.0000       0.0000       0.0000

Previous Body          = None
Degree of Freedom      = 0

Torque about CM        =       0.0000       0.0000       0.0000

Force at CM            =       0.0000       0.0000       0.0000

Hinge spring stiffness =       0.0000       0.0000       0.0000

Hinge spring damping   =       0.0000       0.0000       0.0000

Constant Alignment     =       1.0000       0.0000       0.0000
Matrix                         0.0000       1.0000       0.0000
                               0.0000       0.0000       1.0000
-----------------------------------------------------------------------
Body 2: Link
-----------------------------------------------------------------------
Inertia                =       1.0000       0.0000       0.0000
                               0.0000       1.0000       0.0000
                               0.0000       0.0000       1.0000

Mass                   =       2.0000

CM Location            =       0.0000       0.5000       0.0000

Vector to Hinge        =       2.0000       0.0000       0.0000

Previous Body          = 1 Core
Degree of Freedom      = 2

Torque about CM        =       0.1000 Force at CM            =       0.0000       0.0000       0.0000

Hinge spring stiffness =       0.0000 Hinge spring damping   =       0.0000 Constant Alignment     =       1.0000       0.0000       0.0000
Matrix                         0.0000       1.0000       0.0000
                               0.0000       0.0000       1.0000
-----------------------------------------------------------------------
Body 3: Payload
-----------------------------------------------------------------------
Inertia                =       3.0000       0.0000       0.0000
                               0.0000       3.0000       0.0000
                               0.0000       0.0000       1.0000

Mass                   =       5.0000

CM Location            =       0.0000       0.0000       0.5000

Vector to Hinge        =       1.0000       0.0000       0.0000

Previous Body          = 2 Link
Degree of Freedom      = 3

Torque about CM        =       0.0000 Force at CM            =       0.0000       0.0000       0.0000

Hinge spring stiffness =       0.0000 Hinge spring damping   =       0.0000 Constant Alignment     =       1.0000       0.0000       0.0000
Matrix                         0.0000       1.0000       0.0000
                               0.0000       0.0000       1.0000
  
-----------------------------------------------------------------------
Tree Properties
-----------------------------------------------------------------------
Gravity gradient off
-----------------------------------------------------------------------
Mass                      =     107.0000
-----------------------------------------------------------------------
Active degrees of freedom = 5
-----------------------------------------------------------------------

Reduced mass matrix

  6.5421e-02
 -1.8692e-02
 -4.6729e-02
 -9.3458e-01
  9.8131e-01
 -4.6729e-02
 -9.3458e-01
 -1.8692e-02
  9.5327e-01
-----------------------------------------------------------------------

Paths to Core
-------------
Body 1
1 
Body 2
2 
1 
Body 3
3 
2 
1 
-----------------------------------------------------------------------

Bodies in aggregates
--------------------
Aggregate 1
1 
2 
3 
Aggregate 2
2 
3 
Aggregate 3
3 
-----------------------------------------------------------------------

Plotting and initialization

%----------------------------
tSim        = 20;
dTSim       = 0.1;
nSim        = floor(tSim/dTSim);
hPlot       = zeros(1,nSim);
tPlot       = zeros(1,nSim);
xPlot       = zeros(length(x),nSim);
t           = 0;

Initialize the time display

%----------------------------
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, [], 0, dTSim, 'Tree Sim' );

Run the simulation

%-------------------
for k = 1:nSim

  % Display the status message
  %---------------------------
  [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dTSim );

  % Save for plotting
  %------------------
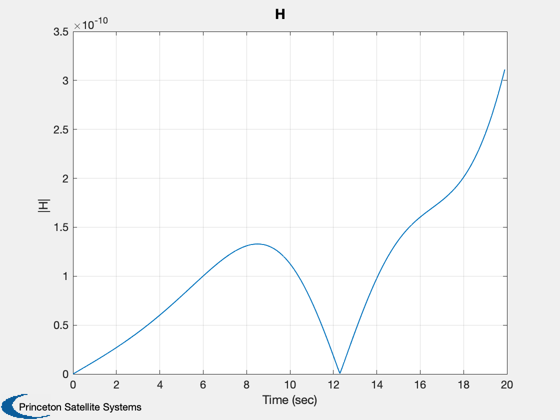
  hPlot(k)   = Mag( TreeH( x, t, treeDS, body ) );
  xPlot(:,k) = x;
  tPlot(k)   = t;

  % Update the equations of motion
  %-------------------------------
  x = RK4( 'Tree', x, dTSim, t, treeDS, body );
  t = t + dTSim;

  % Time control
  %-------------
  switch simulationAction
    case 'pause'
      pause
      simulationAction = ' ';
    case 'stop'
      return;
    case 'plot'
      break;
  end

end

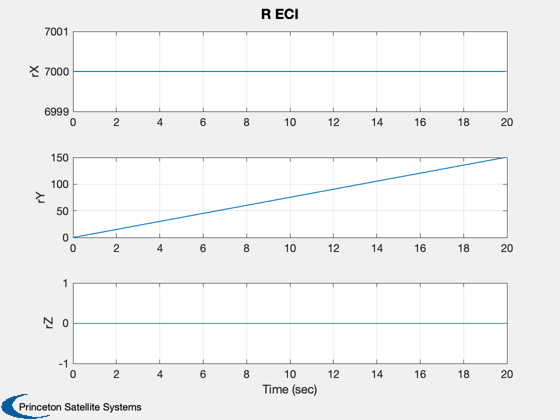
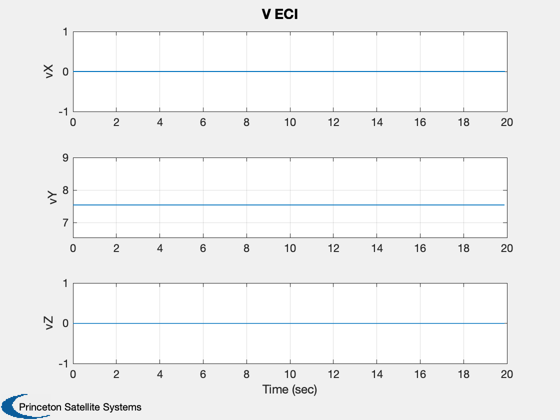
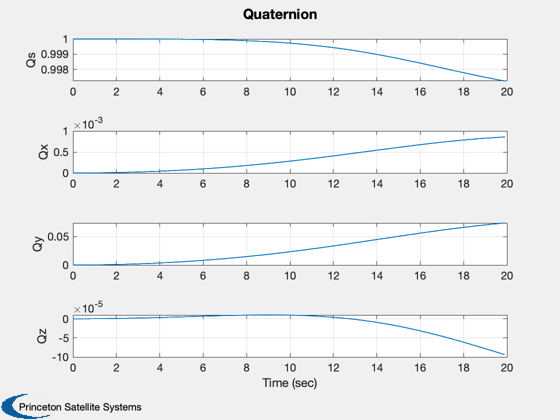
TreePlot( tPlot, xPlot, treeDS, body, hPlot )


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Max Momentum Error =   3.1148e-10 Nms

Published with MATLAB® R2020a