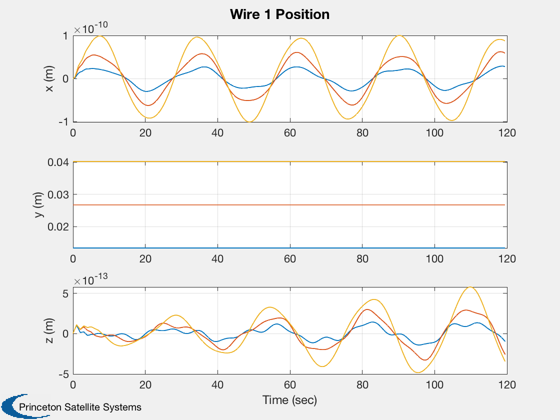
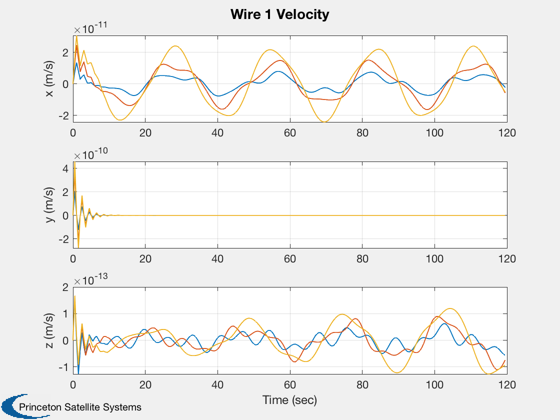
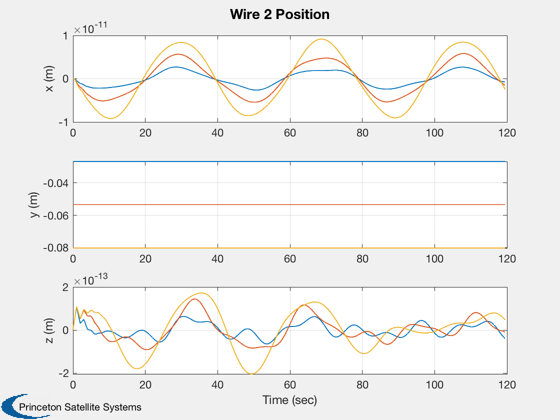
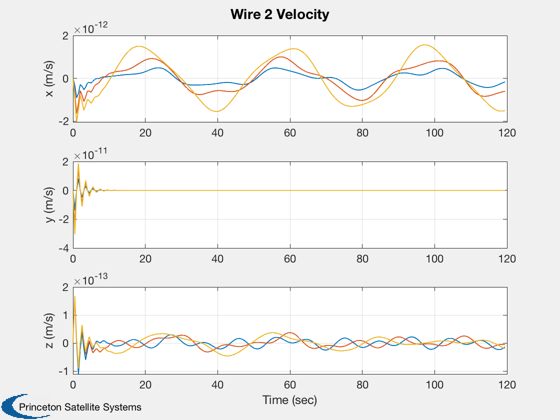
This script demonstrates the deployment of the wire from the spacecraft.

This model assumes that the center-of-mass of the spacecraft does not move as the wires deploy. The simulation models the wire as a string of masses connected by springs. Orbit dynamics and gravity gradient are included.

Since version 2.
-------------------------------------------------------------------------
See also NPlot, Plot2D, TimeGUI, RK4, KConst, WireDMch, WireH,
WireInit, WirePlot, WireDS
-------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
% Copyright  1997 Princeton Satellite Systems, Inc. All rights reserved.
%--------------------------------------------------------------------------

Global for the time GUI

%-------------------------
global simulationAction
simulationAction = ' ';
clear penalty;

Constants

%-----------
false  =  0;
true   =  1;

Simulation parameters

%-----------------------
tSim      = 120.0;
dT        = 0.125;
nSim      = tSim/dT;
nPlot     = min([tSim/dT 200]);
nPMax     = floor(nSim/nPlot);
nPlot     = floor(nSim/nPMax);
gGOn      = false;
kConst    = true;

Print the time to go message every nTTGo steps

%------------------------------------------------
nTTGo     = 1000;

Spacecraft properties

%-----------------------
mass      = 800; % kg
r0        = [0;0;0];
inertia   = [104 0 0;0 107.8 0;0 0 125.4];

muEarth       = 3.98600436e5;

Initial rigid body state

%--------------------------
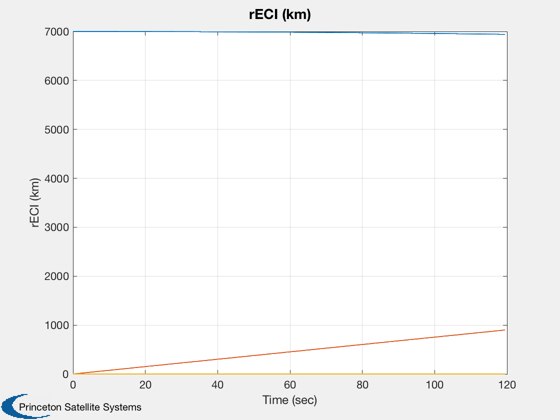
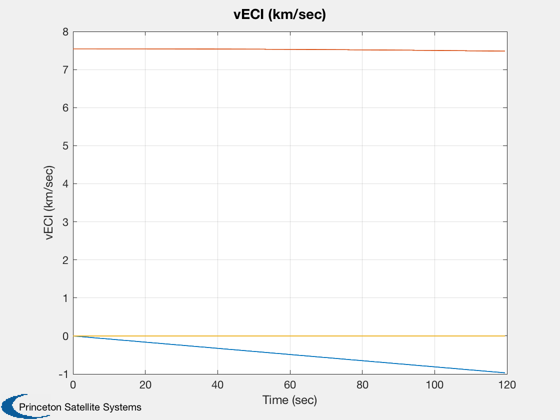
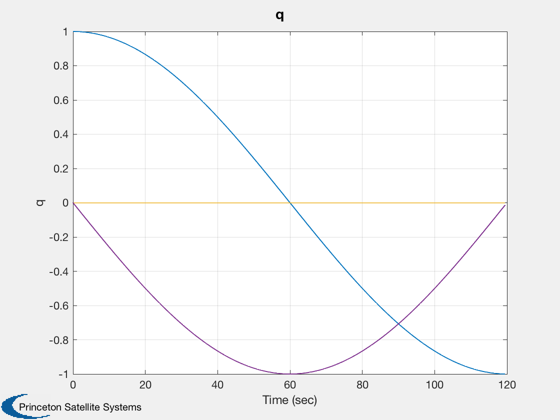
rECI          = [7000;0;0];
vECI          = [0;sqrt(muEarth/7000);0];
omega         = [0;0;0.5]*pi/30;
q             = [1;0;0;0];
torque        = [0;0;0]; % On the central body
force         = [0;0;0]; % On the central body

The wire model. Each column is one wire

%-----------------------------------------
nNodes        = [ 3     3 ];
rWireBase     = [0 0;0.6 -0.6;0 0];
lWireMax      = [0.04 0.08];
massWire      = [0.4 0.4];
kSpring       = [ 3.0   3.0];  % Used only by WireFRB
cSpring       = [ 0.5   0.5 ]; % Used only by WireFRB
cDeploy       = cSpring;       % Used only by WireFRB
nodeDeploying = [ 0     0   ]; % To start undeployed set these to 3
vDeploy       = [ 0.001  0.001 ]; % m/sec

Initialize the wire data structure

%------------------------------------
[wireDS, x] = WireInit( nNodes, mass, massWire, lWireMax, kSpring, cSpring, vDeploy,...
					    cDeploy, nodeDeploying, rWireBase, rECI, vECI, q, omega,...
						r0, inertia, gGOn );

If using the kinematic constraints

%------------------------------------
penalty.alpha = 1e6;
penalty.mu    = 1;
penalty.omega = 10;
penalty.nIts  = 2;

Plotting arrays

%-----------------
xPlot = zeros(length(x),nPlot);
hPlot = zeros(1,nPlot);
tPlot = zeros(1,nPlot);
nP    = 0;
kP    = 0;

t     = 0;

Initialize the time display

%-----------------------------
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, [], 0, dT, 'WireSimG' );

for k = 1:nSim

  % Display the status message
  %---------------------------
  [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT );

  % Plotting
  %---------
  if( nP == 0 )
    kP           = kP + 1;
    xPlot(:,kP)  = x;
    hPlot(kP)    = WireH( x, wireDS );
	tPlot(kP)    = t;
    nP           = nPMax - 1;
  else
    nP           = nP - 1;
  end

  % Choose either the extensional stiffness or constrained wire models
  %-------------------------------------------------------------------
  if( kConst == true )
  	x = RK4( 'WireC',   x, dT, t, wireDS, muEarth, torque, force, penalty );
  else
	x = RK4( 'WireFRB', x, dT, t, wireDS, muEarth, torque, force );
  end
  t           = t + dT;
  [wireDS, x] = WireDMch( wireDS, x, t );

  % Time control
  %-------------
  switch simulationAction
    case 'pause'
      pause
      simulationAction = ' ';
    case 'stop'
      return;
    case 'plot'
      break;
  end

end

Output

%--------
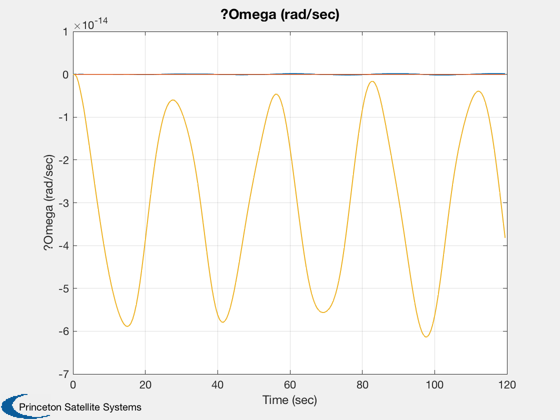
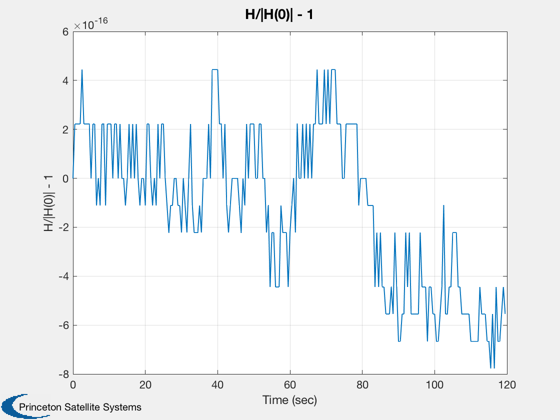
dOmega = [xPlot(11,:) - xPlot(11,1);...
          xPlot(12,:) - xPlot(12,1);...
          xPlot(13,:) - xPlot(13,1)];

magH = abs(hPlot(1));
hPlot = hPlot / magH;

j = 1:kP;
tPlot = tPlot(j);

Plot2D( tPlot, xPlot( 1: 3,j),   'Time (sec)', 'rECI (km)'        );
Plot2D( tPlot, xPlot( 4: 6,j),   'Time (sec)', 'vECI (km/sec)'    );
Plot2D( tPlot, xPlot( 7:10,j),   'Time (sec)', 'q'                );
Plot2D( tPlot, dOmega(:,j),      'Time (sec)', '?Omega (rad/sec)' );
Plot2D( tPlot, hPlot(j) - 1,     'Time (sec)', 'H/|H(0)| - 1'     );

WirePlot( xPlot(:,j), tPlot, wireDS );

fprintf('Max momentum change = %12.4e with dT = %8.4f and tSim = %8.4f\n',max(abs(hPlot-1)), dT, tSim)


%--------------------------------------

Max momentum change =   7.7716e-16 with dT =   0.1250 and tSim = 120.0000

Published with MATLAB® R2019a