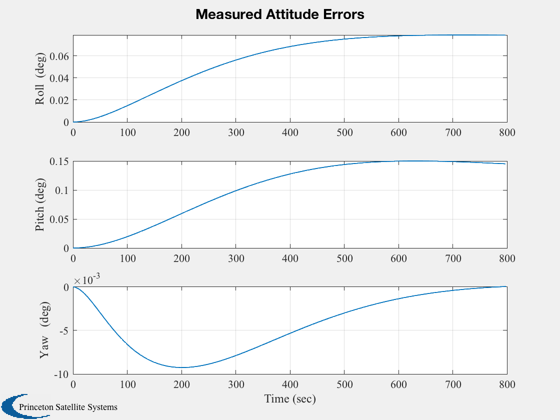
Simulate a momentum bias spacecraft with magnetic roll/yaw control.

The orbit is modeled and the spacecraft controls errors with respect to the LVLH frame. ------------------------------------------------------------------------- Specification ------------------------------------------------------------------------- The controller uses the momentum wheel to control pitch and magnetic torquer control for roll and yaw. The 3-axis controller is a 3-axis PD and torque demand is handed to the torquers. We assume that the torquers allow linear actuation. For the purposes of the simulation we compute the dipole required to meet the instantaneous torque demand. We ignore the disturbance the torquers create around pitch and also the momentum unloading system. This script is useful for sizing the control system.

The inertia in the three directions are Ix=120, Iy=120 and Iz=1.3. The satellite is in an equatorial orbit so that the field is almost normal to the orbit.

The damping ratios and natural frequencies are:

Tach loop:
zeta = 0.7621
wN= 0.5

Pitch and Roll loop:
zeta = 0.7621
wN   = 0.009

Yaw loop:
zeta = 1.0
wN   = 0.15

------------------------------------------------------------------------- See also IC623X3, PDDesign, PIDesign, QForm, QLVLH, QMult, QPose, Constant, NPlot, Plot2D, TimeGUI, RK4, JD2000, TOrbit, RVFromKepler, MagField, SunV1 -------------------------------------------------------------------------

Global for the TimeGUI
Constants
The control sampling period and the simulation integration time step
Number of sim steps
Plot every nPMax steps
spacecraft with respect to the sun projection in the orbit plane
Spacecraft Inertias
Wheel spin axis unit vector
Design the control loops
Tach loop
Attitude Loops
Initialize the control system
The sun sensors along +X and -X
Plotting arrays
Initialize the time display
Magnetic field
Generate the orbit
el = [a,i,W,w,e,M].
Initial conditions at equinox
Initial conditions
Get a step response
Run the simulation
Plotting

%--------------------------------------------------------------------------
%   Copyright (c) 1999, 2007, 2016 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 5.5 (2003)
%   2016.1 Switch to newer IGRF11 model (from 1995 data) for the Earth
%--------------------------------------------------------------------------

Global for the TimeGUI

%------------------------
global simulationAction
simulationAction = ' ';

Constants

%----------
degToRad    = Constant('deg to rad');
radToDeg    = Constant('rad to deg');

The control sampling period and the simulation integration time step

%--------------------------------------------------------------------
tSamp       = 2;

Number of sim steps

%--------------------
nSim        = 400;
tEnd        = nSim*tSamp;

Plot every nPMax steps

%----------------------
nPMax       = 1;
nPlot       = nSim/nPMax;

% Sun angle with respect to the orbit plane and location of the

spacecraft with respect to the sun projection in the orbit plane

%----------------------------------------------------------------
rOrbit      = 6700;
mu          = 3.98600436e5;

Spacecraft Inertias

%--------------------
inr         = IC623X3( [120 120 1.3 0 0 0] );
inrRWA      = 0.01; % A guess
invInr      = inv(inr);

Wheel spin axis unit vector

%----------------------------
uW          = [0;1;0];

%--------------------------------------------------------------------------

Design the control loops

%--------------------------------------------------------------------------

Tach loop

%----------
[aTL,bTL,cTL,dTL] = PIDesign( 0.7621,  0.5, inrRWA, tSamp );

Attitude Loops

%--------------
[aRoll ,bRoll, cRoll, dRoll]  = PDDesign( 0.7621, 0.009, 0.09, inr(1,1), tSamp );
[aPitch,bPitch,cPitch,dPitch] = PDDesign( 0.7621, 0.009, 0.09, inr(2,2), tSamp );
[aYaw,  bYaw,  cYaw,  dYaw]   = PDDesign( 1.0,    0.15,  1.5,  inr(3,3), tSamp );

Initialize the control system

%-----------------------------
xTL             = zeros(size(aTL,   1),1);
xRoll           = zeros(size(aRoll, 1),1);
xPitch          = zeros(size(aPitch,1),1);
xYaw            = zeros(size(aYaw,  1),1);
tC              = [0;0;0];
wBias           = 100; % Momentum wheel bias rate
xEst            = [2;2;2]*pi/180;
rEst            = [0.1 0.1 0.1 0.1 0.1 0.1 0.1];
fScale          = 1;
p               = 10*eye(3);

The sun sensors along +X and -X

%--------------------------------
qBToS   = [cos(pi/4)  cos(pi/4);...
                   0          0;...
           sin(pi/4) -sin(pi/4);...
                   0          0];
fOV     = [60 60;60 60]*degToRad;
uS      = [0 0;0 0;1 1];

Plotting arrays

%----------------
cPlot      = zeros( 4,nPlot);
ePlot      = zeros( 3,nPlot);
tPlot      = zeros( 1,nPlot);
xPlot      = zeros( 8,nPlot);
pPlot      = zeros( 3,nPlot);
vPlot      = zeros( 3,nPlot);
mPlot      = zeros( 3,nPlot);
rVPlot     = zeros( 6,nPlot);
bPlot      = zeros( 3,nPlot);
dTSim      = tSamp;
t          = 0;
nP         = 0;
kP         = 0;

Initialize the time display

%----------------------------
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, [], 0, dTSim, 'MagSim' );

Magnetic field

%---------------
magFieldData = load('IGRF11');

Generate the orbit

%-------------------
tOrbit = (0:(nSim-1))*dTSim;

el = [a,i,W,w,e,M].

%--------------------
[rECI, vECI] = RVFromKepler( [rOrbit 0 0 0 0 0], tOrbit );

Initial conditions at equinox

%------------------------------
jD     = JD2000 + tOrbit/86400 + 1000;

Initial conditions

%-------------------
%                  q         w     wRWA
x      = [ QLVLH( rECI(:,1), vECI(:,1) ); [0;-sqrt(mu/rOrbit^3);0]; 100 ];
uSun   =  SunV1( jD, rECI );

Get a step response

%--------------------
tDist   = [10;10;0]*1.e-6;
tWF     = 0.0;
tW      = 0;
mDipole = zeros(3,1);

Run the simulation

%------------------
for k = 1:nSim

  qECIToBody = x(1:4);

  qLVLH      = QLVLH( rECI(:,k), vECI(:,k) ); % The local vertical frame

  % qLVLH  transforms from ECI to LVLH
  % We want LVLH to Body
  %-----------------------------------
  qLVLHToBody = QMult(  QPose( qLVLH ), qECIToBody );

  if( qLVLHToBody(1) < 0 )
    qLVLHToBody = - qLVLHToBody;
  end

  % Small angles
  %-------------
  roll  = -2*qLVLHToBody(2);
  pitch = -2*qLVLHToBody(3);
  yaw   = -2*qLVLHToBody(4);

  % Display the status message
  %---------------------------
  [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dTSim );

  % The magnetic field
  %-------------------
  b                = MagField( rECI(:,k), jD, 5, magFieldData.g, magFieldData.h );
  bMeas            = QForm( qECIToBody, b );

  % Plotting
  %--------
  if( nP == 0 )
    kP           = kP + 1;
    xPlot(:,kP)  = x;
    tPlot(1,kP)  = t;
    cPlot(:,kP)  = [tC;tW];
    ePlot(:,kP)  = [roll;pitch;yaw]*radToDeg;
    rVPlot(:,kP) = [rECI(:,k);vECI(:,k)];
    bPlot(:,kP)  = b;
    mPlot(:,kP)  = mDipole;
    nP           = nPMax - 1;
  else
    nP           = nP - 1;
  end

  wTach = x(8); % Perfect tachometer

  % The attitude control loops
  %--------------------------
  tC(1)  = -cRoll*xRoll - dRoll*roll;
  xRoll  =  aRoll*xRoll + bRoll*roll;

  tC(2)  = -cPitch*xPitch - dPitch*pitch;
  xPitch =  aPitch*xPitch + bPitch*pitch;

  tC(3)  = -cYaw*xYaw - dYaw*yaw;
  xYaw   =  aYaw*xYaw + bYaw*yaw;

  tD     = tC; % What we actually pass to the sim

  % The torquers supply roll and yaw torques
  % Our controller only uses the body y-field
  % This will lead to disturbance in pitch which we are going to ignore
  %--------------------------------------------------------------------
  mDipole(1) =  tC(3)/bMeas(3);
  mDipole(3) = -tC(1)/bMeas(3);

  % The bias momentum is adjusted by the torque demand for pitch
  %-------------------------------------------------------------
  dWBias = -tC(2)/inrRWA; % Note we flip the sign
  tD(2)  = 0; % Our magnetic torquer loops will not handle this now
  wBias  = wBias + dWBias;

  % The MWA Tach Loops
  %------------------
  wError =  wTach - wBias;
  tW     = -dTL*wError - cTL*xTL;
  xTL    =  aTL*xTL + bTL*wError;

  %------------------------------------------------------------------------
  % Update the equations of motion
  %------------------------------------------------------------------------
  x        = RK4( 'FMagSim', x, dTSim, t, inr, invInr, tDist + tD, inrRWA, uW, tW+tWF );
  t        = t  + dTSim;
  jD       = jD + dTSim/86400;

  % Time control
  %-------------
  switch simulationAction
    case 'pause'
      pause
      simulationAction = ' ';
    case 'stop'
      return;
    case 'plot'
      break;
  end

end

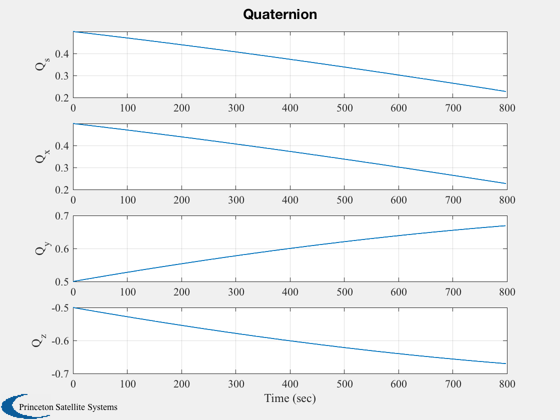
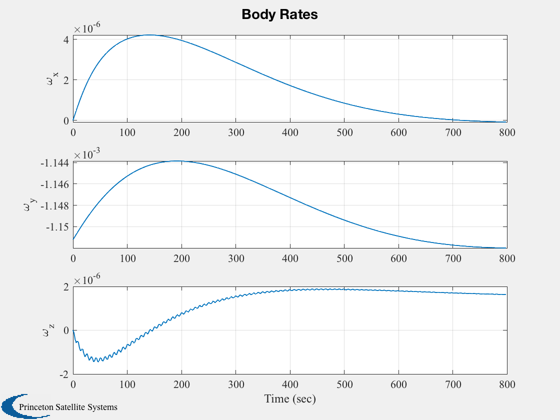
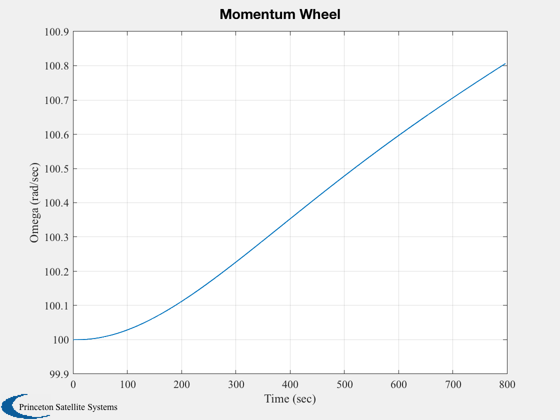
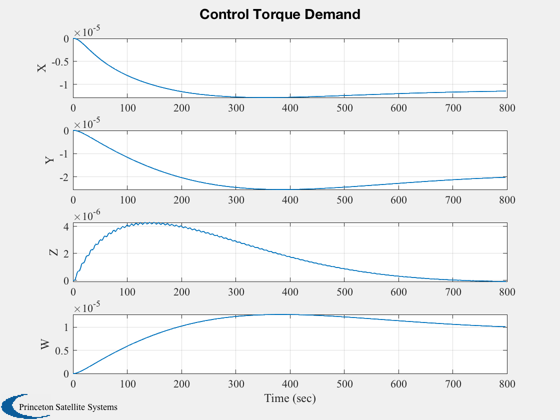
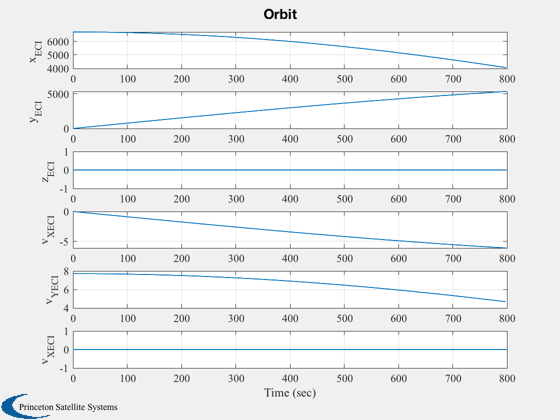
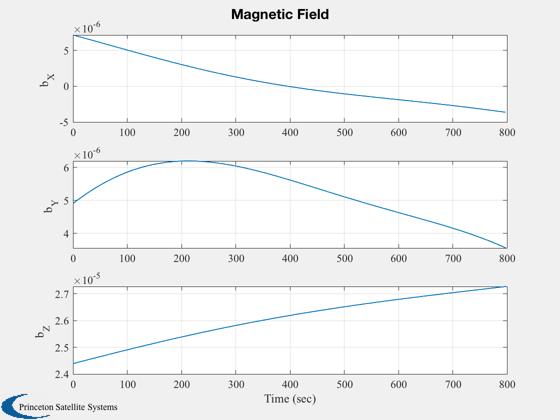
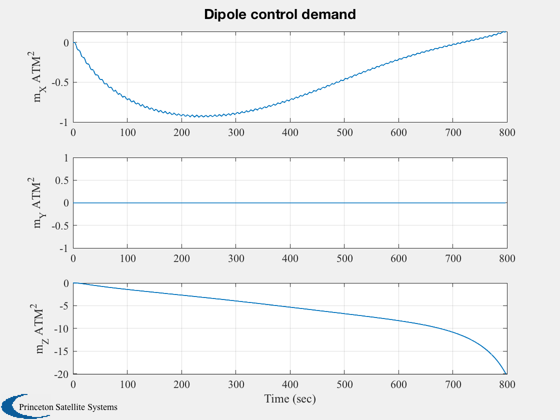
Plotting

%---------
xLbl = 'Time (sec)';

j = 1:kP;

tPlot = tPlot(j);

Plot2D( tPlot, xPlot(1:4,j),xLbl,['Q_s';'Q_x';'Q_y';'Q_z'],'Quaternion')
Plot2D( tPlot, xPlot(5:7,j),xLbl,['\omega_x';'\omega_y';'\omega_z'],'Body Rates')
Plot2D( tPlot, xPlot(8,j),  xLbl,'Omega (rad/sec)','Momentum Wheel')
Plot2D( tPlot, cPlot(:,j),  xLbl,['X';'Y';'Z';'W'],'Control Torque Demand')
Plot2D( tPlot, ePlot(:,j),  xLbl,['Roll  (deg)';'Pitch (deg)';'Yaw   (deg)'],'Measured Attitude Errors')
Plot2D( tPlot, rVPlot(:,j), xLbl,{'x_{ECI}';'y_{ECI}';'z_{ECI}';'v_{XECI}';'v_{YECI}';'v_{XECI}'},'Orbit')
Plot2D( tPlot, bPlot(:,j),  xLbl,['b_X ';'b_Y ';'b_Z '],'Magnetic Field')
Plot2D( tPlot, mPlot(:,j),  xLbl,['m_X ATM^2';'m_Y ATM^2';'m_Z ATM^2'],'Dipole control demand')


%--------------------------------------