Demonstrates magnetic control and power profiles.

Six DOF simulation with point mass orbit, rigid body dynamics, and the magnetic torque handled explicitly in the RHS. Satellite is modeled with three magnetic torquers and four solar panels. ------------------------------------------------------------------------- See also MagField and FRBWithMag, QForm, Constant, NPlot, Plot2D, Plot3D, PrintFig, TimeGUI, TimeLabl, RK4, Date2JD, OrbRate, El2RV, PltOrbit, Eclipse, SunV1 -------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 1995-2004, 2008, 2016 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   2016.1 Switch to newer IGRF11 model (from 1995 data) for the Earth. Also
%   change RHS to a function handle.
%--------------------------------------------------------------------------

clear d

Print plots to eps file

%-------------------------
printPlots = 0;

Global for the TimeGUI

%------------------------
global simulationAction
simulationAction = ' ';

Constants

%-----------
degToRad    = pi/180;
radToDeg    = 180/pi;
c45         = cos(45*degToRad);

Power system - 4 solar panels

%-------------------------------
% assume same area and efficiency for all panels
pEff        = 0.15;
pSun        = 1367; % solar flux, Watts/m^2
areaPanel   = 0.2;  %m^2
fPanel      = pEff*pSun*areaPanel;
uPanel      = [1 0 0 -1;0 1 -1 0;0 0 0 0]; % 4 unit vectors

Torquers

%----------
mTorquer    = 10*eye(3); % 3 orthogonal torquers
uDipole     = [0;0;1]; % The control (on/off flags)

The control sampling period and the simulation integration time step

---------------------------------------------------------------------

dTSim       = 1; % sec

Number of sim steps

--------------------

nSim        = 6000; % sec
tEnd        = nSim*dTSim;

Plot every nPMax steps

-----------------------

nPMax       = 1;
nPlot       = nSim/nPMax;

Print the time to go message every nTTGo steps

%------------------------------------------------
nTTGo       = 100;

Gravity model

%---------------
d.mu        = Constant('mu earth');

The external disturbance model

-------------------------------

d.tExt      = [0.0;0.0;0.0];

Spacecraft inertia

-------------------

d.inr       = [2000,0,0;0,4000,0;0,0,2000];
d.invInr    = inv(d.inr);

Plotting arrays

----------------

tPlot      = zeros( 1,nPlot);
xPlot      = zeros(26,nPlot);

Magnetic field

%----------------
magFieldData = load('IGRF11');

Epoch

%-------
jD         = Date2JD([2004 7 21 0 0 0]); % Julian date

Orbit

%-------
sma        = 7000;  % km
inc        = 0.5;   % rad
el         = [sma inc 0 0 0 0];
[r0,v0]    = El2RV(el);
PltOrbit( el, jD );

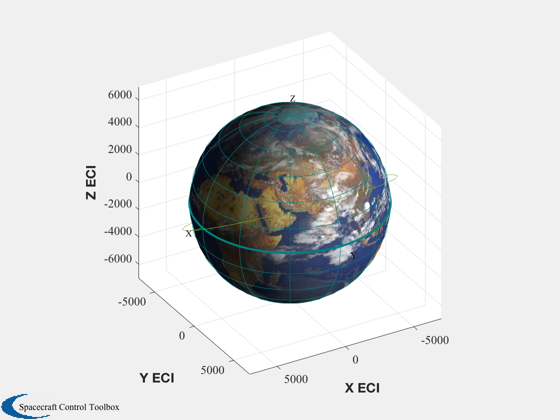
OrbRate function -

r is radius; d.mu is Gravitational parameter;

Orbit_Rate = @( r ) sqrt(d.mu*(2./r - 1./r))./r;

Initial conditions [r;v;q;omega]

%----------------------------------
q0         = [1;0;0;0]; % ECI to body frame
w0         = [0;Orbit_Rate(7000);0]; % rad/s
x          = [r0; v0;  q0;  w0]; % r in km and v in km/s
t          = 0;

Plotting controls

%-------------------
nP         = 0;
kP         = 0;

Initialize the time display

%-----------------------------
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, [], 0, dTSim, 'Magnetic Control Sim' );

Run the simulation

-------------------

for k = 1:nSim

  % The sun vector in the body frame
  %---------------------------------
  [uSun,rSun] = SunV1( jD );
  uSunBody = QForm( x(7:10), uSun );
  n = Eclipse( x(1:3), rSun*uSun );

  % Power
  %------
  f      = uSunBody'*uPanel;
  % find panels facing away from sun and set power to zero
  j      = find(f < 0);
  f(j)   = 0;
  % multiply power factor times cos(angle) to the sun, including eclipses
  pPanel = n*fPanel*f;

  % Control - compute total dipole
  %-------------------------------
  d.dipole = [0;0;0];
  for j = 1:length(uDipole)
      if( uDipole(j) == 1 )
          d.dipole = d.dipole + mTorquer(:,j);
      end
  end

  % The magnetic field
  %-------------------
  d.bECI =  MagField( x(1:3), jD, 2, magFieldData );

  % Display the status message
  %---------------------------
  [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dTSim );

  % Integrate one time step
  %------------------------
  x        = RK4( @FRBWithMag, x, dTSim, t, d );

  % Update the time
  %----------------
  t        = t + dTSim;
  jD       = jD + dTSim/86400;

  % Plotting
  % --------
  if( nP == 0 )
    kP          = kP + 1;
    xPlot(:,kP) = [x;d.bECI;pPanel';d.dipole;uDipole];
  	tPlot(kP)   = t;
    nP          = nPMax - 1;
  else
    nP          = nP - 1;
  end

  % Time control
  %-------------
  switch simulationAction
    case 'pause'
      pause
      simulationAction = ' ';
    case 'stop'
      return;
    case 'plot'
      break;
  end

end

Adjust the plotting arrays if you stopped early

%-------------------------------------------------
j     = 1:kP;
tPlot = tPlot(j);
xPlot = xPlot(:,j);

Nice units for time

%---------------------
[tPlot,tL] = TimeLabl( tPlot );

Plotting function

%-------------------
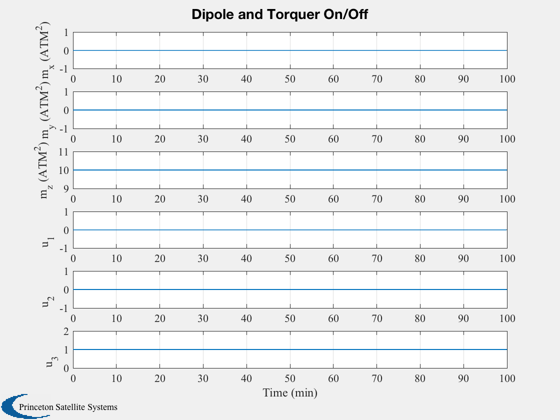
Plot3D( xPlot( 1: 3,:),'R_x (km)','R_y (km)','R_z (km)', 'RECI' );
Plot2D( tPlot, xPlot( 7:10,:), tL, {'Q_s';'Q_x';'Q_y';'Q_z'},                'Quaternion'   )
Plot2D( tPlot, xPlot(11:13,:), tL, {'\omega_x';'\omega_y';'\omega_z'},      'Angular Rates (rad/s)'  )
Plot2D( tPlot, xPlot(14:16,:), tL, {'B_x (T)';'B_y (T)';'B_z (T)'},         'Magnetic Field')
Plot2D( tPlot, xPlot(17:20,:), tL, {'P_1 (W)';'P_2 (W)';'P_3 (W)'; 'P_4 (W)'}, 'Power Generated by Panels')
Plot2D( tPlot, xPlot(21:26,:), tL, {'m_x (ATM^2)'  'm_y (ATM^2)' 'm_z (ATM^2)' 'u_1'  'u_2' 'u_3'}, 'Dipole and Torquer On/Off')

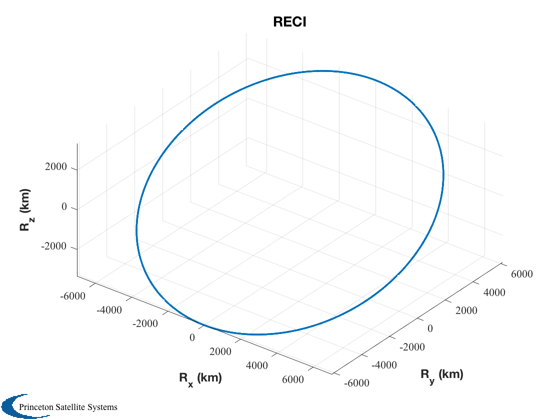
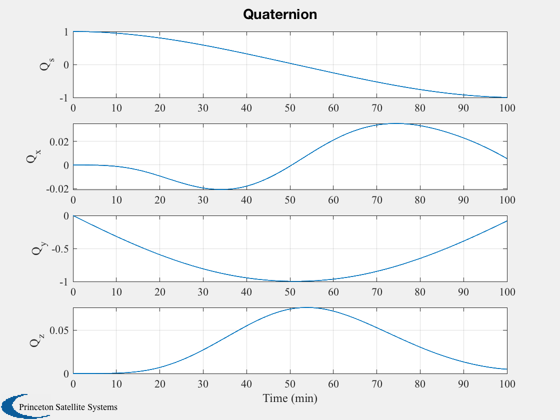
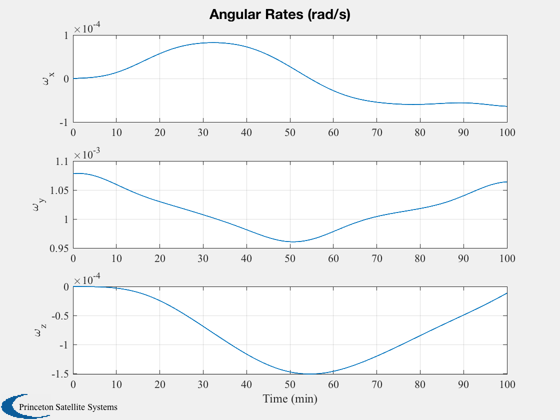
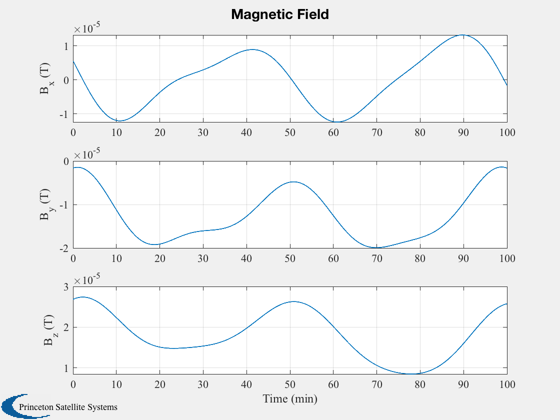
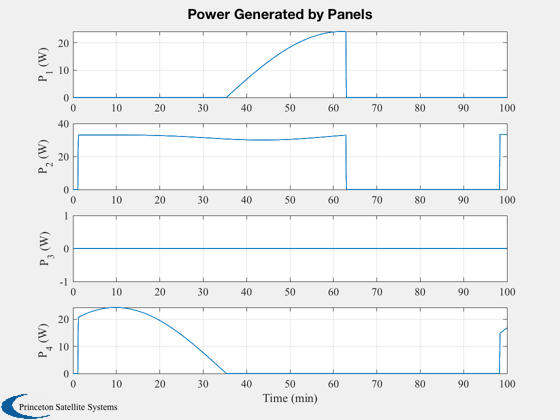
Save plots as eps files

%-------------------------
if( printPlots )
  PrintFig(0,1,1,'Mag_R');
  PrintFig(0,1,2,'Mag_V');
  PrintFig(0,1,3,'Mag_Q');
  PrintFig(0,1,4,'Mag_Omega');
  PrintFig(0,1,5,'Mag_B');
  PrintFig(0,1,5,'Power');
end


%--------------------------------------

Published with MATLAB® R2019a