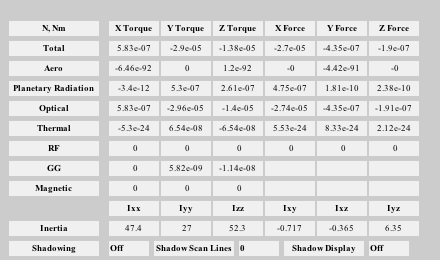
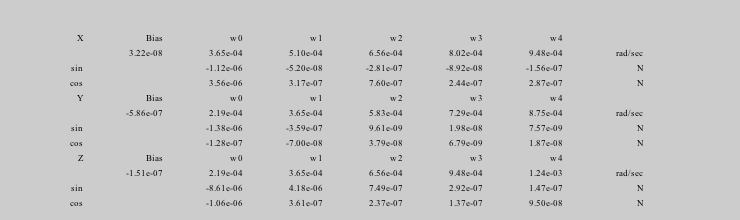
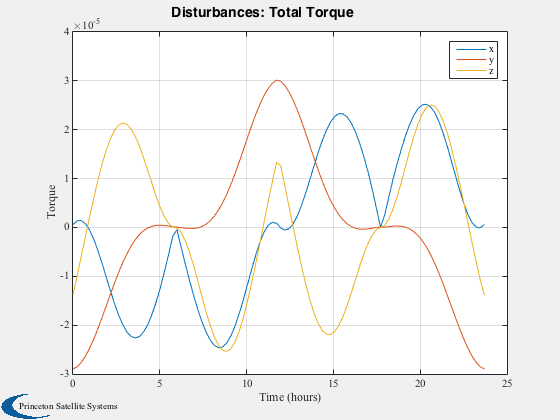
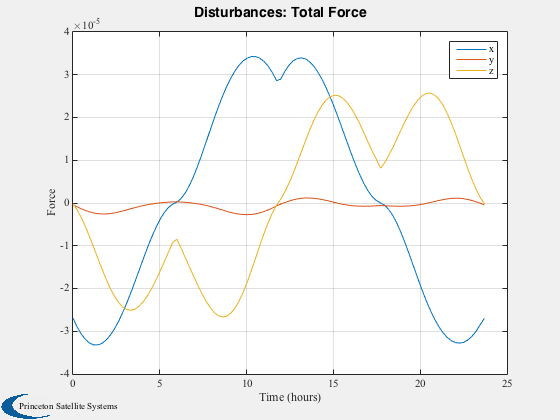
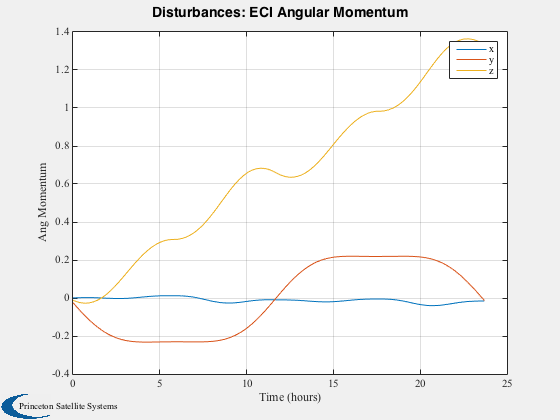
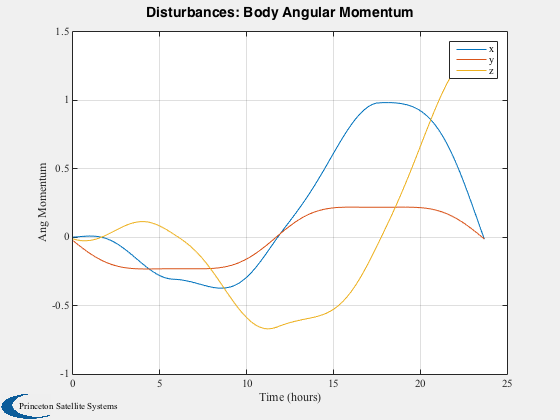
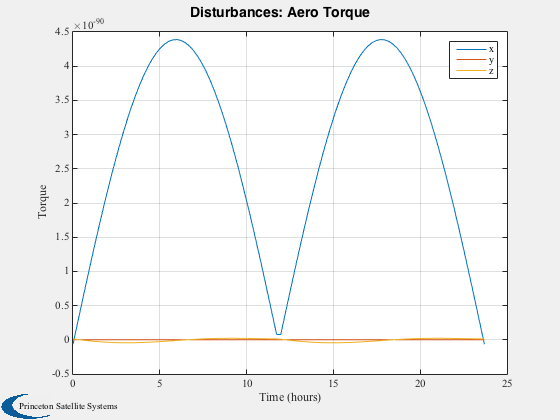
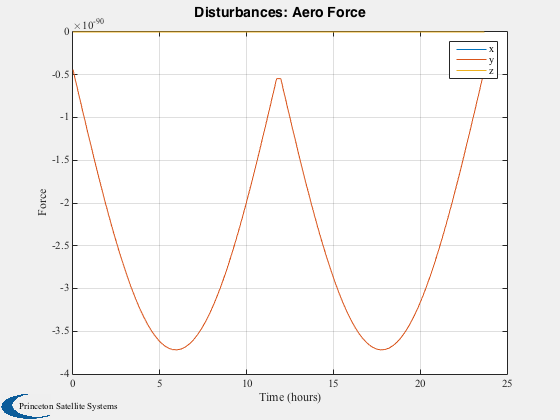
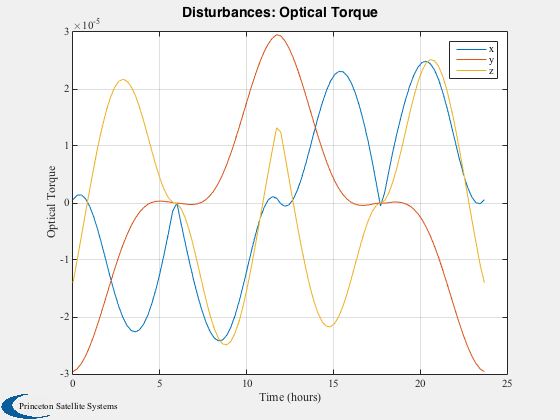
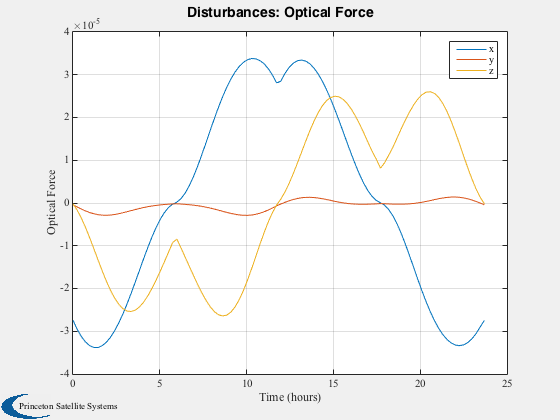
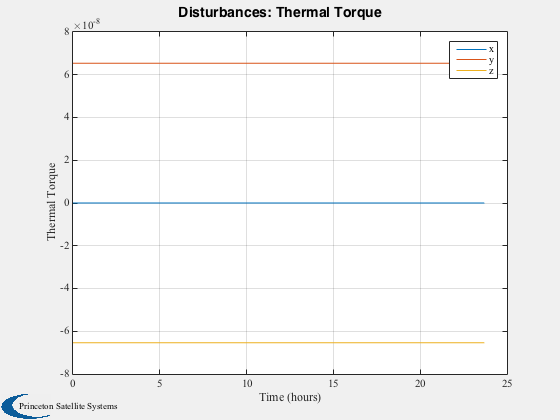
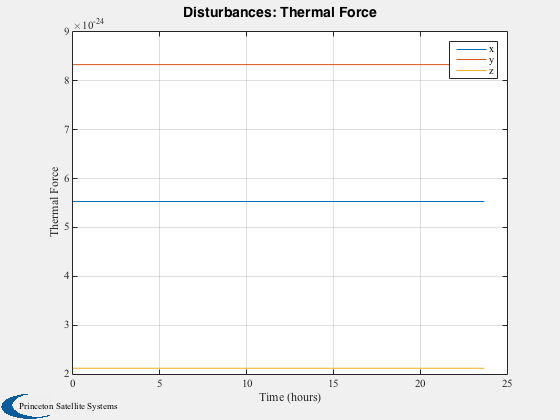
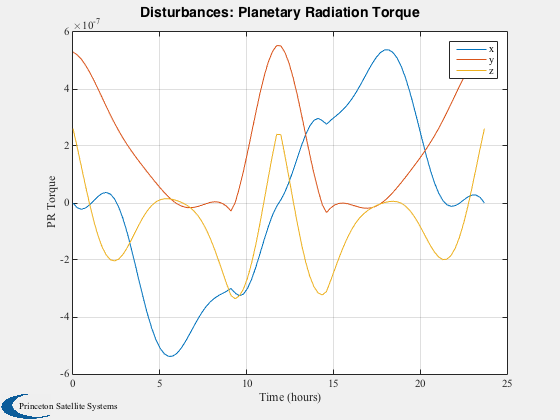
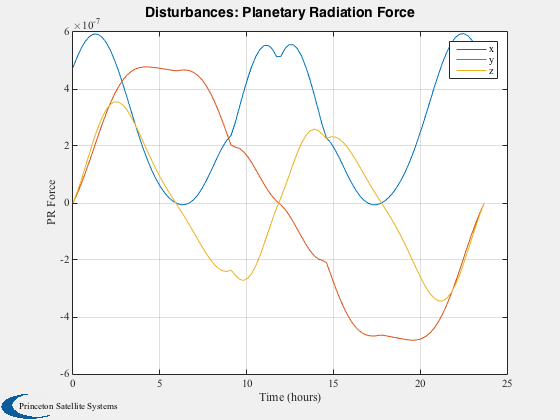
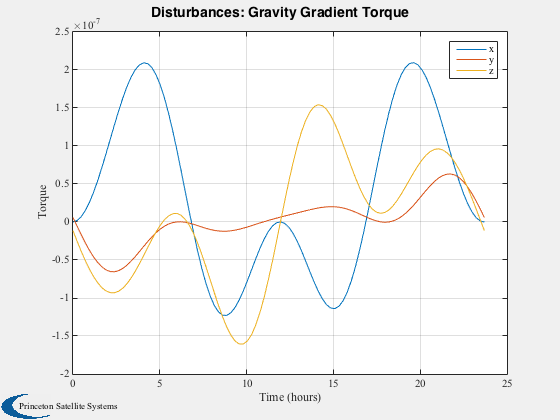
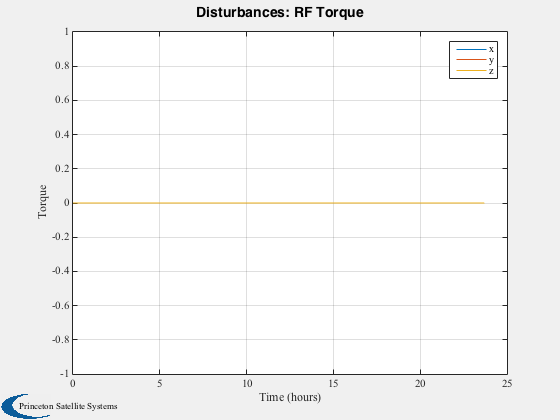
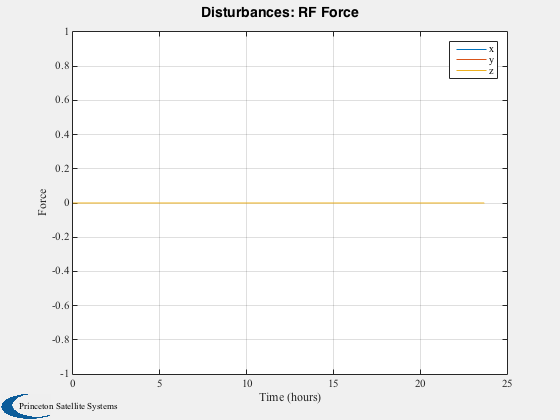
Run the disturbance model in GEO. Uses TwoArraySC.mat

------------------------------------------------------------------------
See also Q2Mat, QLVLH, Constant, Date2JD, Period, Disturbances, SunV1
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%  	Copyright (c) 1998-2003 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

% Load the model
%-----------------------
g = load('TwoArraySC');
DrawSCPlanPlugIn(g);

% Ephemeris
%----------
jD           = Date2JD([3 22 2001 0 0 0]); % Equinox
[uSun, rSun] = SunV1( jD );

% Disturbances parameters
%------------------------
d           = Disturbances( 'defaults' );
solarFlux   = 1367; % Watts/m^2
d.s         = solarFlux*uSun;
d.shadow    = 0;
d.units     = 'm';
d.planet    = 'earth';
d.mu        = Constant('mu earth');

% Initialize the disturbance model
%---------------------------------
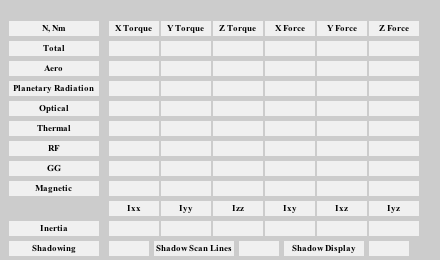
hD = Disturbances( 'init', g, d );

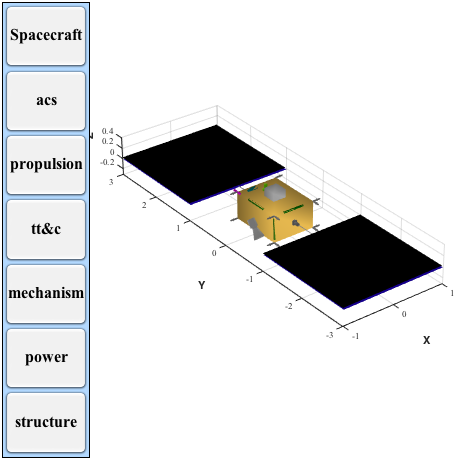
Prepare 100 samples in a circular orbit

%-----------------------------------------
nSamp       = 100;
rOrbit      = 42167;
period      = Period(rOrbit);
d.tSamp     = period/nSamp;
theta       = linspace(0,2*pi,nSamp);
c           = cos(theta);
s           = sin(theta);

% A circular orbit
%-----------------
d.r         = rOrbit*[c;s;zeros(1,nSamp)];
v           = sqrt(d.mu/rOrbit)*[-s;c;zeros(1,nSamp)];
qLVLH       = QLVLH( d.r, v );

% Create the transformation matrix arrays
% In this case we are using angles and
% axes.
%----------------------------------------
for k = 1:nSamp
  g.body(1).bHinge(k).angle = theta(k);
  g.body(1).bHinge(k).axis  = 2;
  g.body(2).bHinge(k).angle = theta(k);
  g.body(2).bHinge(k).axis  = 2;
  g.body(3).bHinge(k).b     = Q2Mat( qLVLH(:,k) )';
end

Run

Disturbances( 'run', g, d, hD );
Figui;


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b