Contents

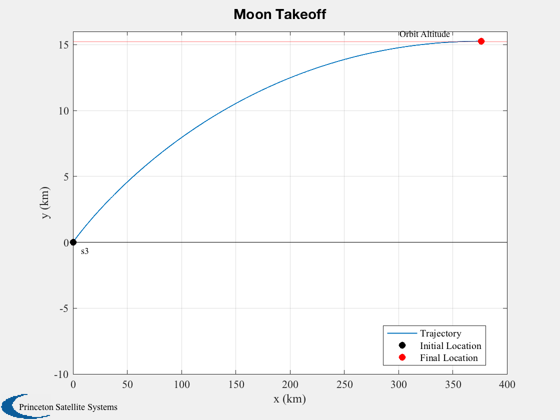
Takeoff demo using bilinear tangent thrust programming.

%--------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2013-2014 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 2014.1
%--------------------------------------------------------------------------

Setup

% Select the body for launch
%---------------------------
body = 'Moon'; % 'Mars'

% These are in km
%----------------
switch body
    case 'Mars' % Mars
        mu          = Constant('mu mars');
        rMars       = Constant('equatorial radius mars');
        u           = sqrt(mu/rMars);
        g           = mu/rMars^2;
        h           = 200;

    case 'Moon'
        u           = 1.8654;
        g           = 1.6154e-3;
        h           = 15.240;
end

% Number of simulation steps
%---------------------------
n           = 2000;

% Thrust acceleration
%--------------------
a           = 3*g;

% Find the thrust direction angles
%---------------------------------
TolX        = 1e-7; TolFun = 1e-11; MaxFunEvals = 2500;
Options     = optimset('TolX',TolX,'TolFun',TolFun,'MaxFunEvals',MaxFunEvals);


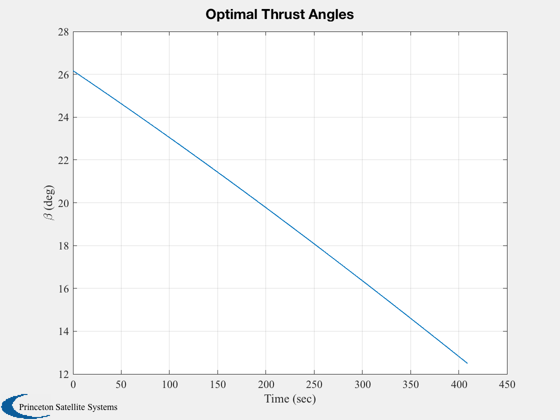
[beta, t]	= BilinearTangentLaw( u, g, a, h, n, Options );
              BilinearTangentLaw( u, g, a, h, n, Options );

dT          = t(2) - t(1);

% Size the array
%---------------
xP          = zeros(4,n);

% Initial state
%--------------
x           = [0;0;0;0];

Simulate

%----------
for k = 1:n
    xP(:,k)	= x;
    x       = RK4('RHSPlanetTakeoff',x,dT,t,a,g,beta(k));
end

Plot

%------
[t, tL] = TimeLabl(t);

% Titles for plots
%-----------------
s1 = sprintf('%s Takeoff',body);
s2 = sprintf('%s Takeoff States',body);
s3 = sprintf('%s Surface',body);

Plot2D(xP(1,:),xP(2,:),'x (km)','y (km)',s1);

% Annotate the plot
%------------------
hold on
plot(xP(1,1),xP(2,1),'ko','MarkerFaceColor','k')
plot(xP(1,end),xP(2,end),'ro','MarkerFaceColor','r')
xLim = get(gca,'xlim');
set(gca,'yLim',[-10 floor(1.1*h)])
line(xLim,[0,0],'color','black')
text(xP(1,1)+0.02*xP(1,end),-0.04*h,'s3')
line(xLim,[h;h],'color','red')
text(0.8*xP(1,end),1.04*h,'Orbit Altitude')
legend('Trajectory','Initial Location','Final Location','Location','Best')

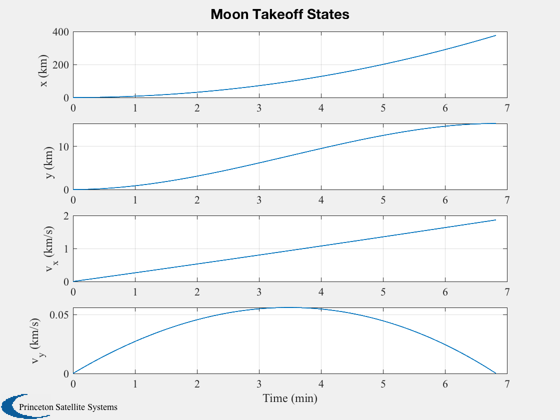
Plot2D(t,xP,tL,{'x (km)','y (km)','v_x (km/s)', 'v_y (km/s)'},s2);


%--------------------------------------

Published with MATLAB® R2019a