BLDCMDemo

Brushless DC motor simulation.
Plot

Brushless DC motor simulation.

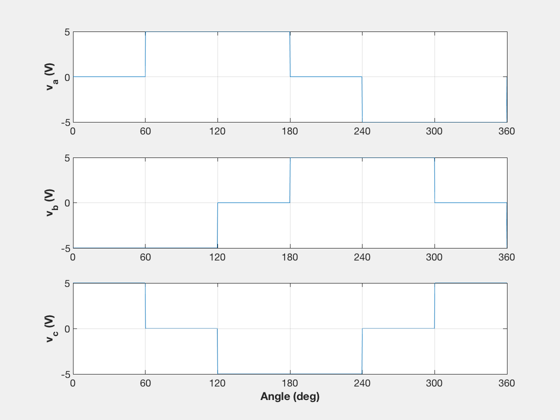
The demo first generates a voltage map for 1 electrical revolution
to show the 6 step commutation. This is typical commutation used
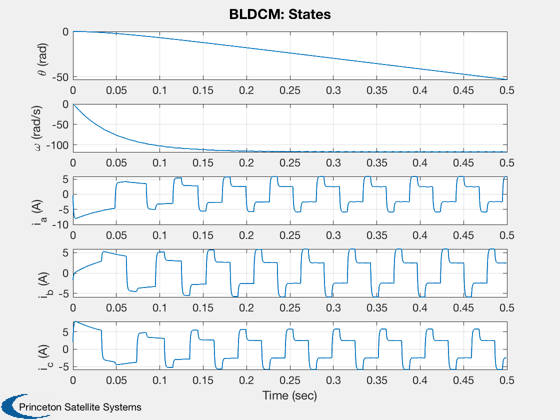
in reaction wheels. These leads to torque noise and poor response
at low speeds. You can see the torque noise in the plots.

%--------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2012 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 11.
%--------------------------------------------------------------------------

dT              = 0.0002;
tEnd            = 0.5;
n               = floor(tEnd/dT);

xP              = zeros(9,n);


% [angle;mechanical angular rate;iA;iB;iC]
%----------------------------------------
x               = [0;0;0;0;0];

d               = struct;
d.r             = 0.6;
d.l             = 0.42e-3;
d.j             = 0.0002;
d.kB            = 0.1;
d.kT            = 0.1;
d.tL            = 0;
d.p             = 2;
d.dEMF.flux     = 0.6; % Tesla
d.dInverter.dir = -1; % Direction
d.dInverter.vS	= 5;
d.dFriction     = [];
d.fEMF          = @BLDCMFlux;
d.fFriction     = @BLDCMFriction;
d.fInverter     = @BLDCMInverter;

% Test the inverter
%------------------
a               = linspace(0,2*pi,1000);
vS              = zeros(3,1000);
hS              = zeros(3,1000);
for k = 1:length(a)
 	thetaE = d.p*a(k)/2;
	f	= [ feval(d.fEMF,thetaE,       d.dEMF);...
        feval(d.fEMF,thetaE-2*pi/3,d.dEMF);...
        feval(d.fEMF,thetaE-4*pi/3,d.dEMF)];

	[v, hS(:,k)] = BLDCMInverter( f, d.dInverter );
	vS(:,k) = v;
end

a = a*180/pi;

hS(1,:) = hS(1,:)*0.8;
hS(2,:) = hS(2,:)*0.6;
hS(3,:) = hS(3,:)*0.4;

c = 'abc';

NewFig('Voltages 2 Pole')
for k = 1:3
    subplot(3,1,k)
    plot(a,vS(k,:))
    grid
    YLabelS(sprintf('v_{%s} (V)',c(k)))
    set(gca,'xlim',[0 360],'xTick',[0 60 120 180 240 300 360]);
end
XLabelS('Angle (deg)')


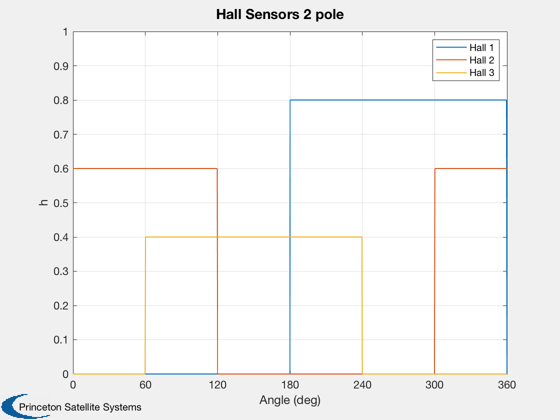
Plot2D(a,hS,'Angle (deg)','h','Hall Sensors 2 pole');
set(gca,'xlim',[0 360],'ylim',[0 1],'xTick',[0 60 120 180 240 300 360]);
legend('Hall 1', 'Hall 2', 'Hall 3')

d.p = 2;

for k = 1:n
    x               = RK4('BLDCMRHS',x,dT,0,d);
    [xDot, tE, v]	= BLDCMRHS( x, 0, d );
    xP(:,k)         = [x;tE;v];
end

Plot

%------
[t, tL] = TimeLabl((0:(n-1))*dT);

Plot2D( t, xP(1:5,:), tL, {'\theta (rad)' '\omega (rad/s)' 'i_a (A)' 'i_b (A)' 'i_c (A)'}, 'BLDCM: States')
Plot2D( t, xP(6:9,:), tL, {'t_E (Nm)' 'v_{a} (V)' 'v_{b} (V)' 'v_{c} (V)' }, 'BLDCM: Torque and Voltages')


%--------------------------------------

Contents

Brushless DC motor simulation.

Plot