Demonstrate a spacecraft in orbit pointing at a target on the Earth

Since version 8.
------------------------------------------------------------------------
See also C2DelZOH, PIDMIMO, AU2Q, CoordinateTransform, LatLonToR, Q2AU,
QForm, QMult, QPose, U2Q, Constant, AnimateVectors, Map, RK4, Unit,
Date2JD, JD2T, OrbRate, RVFromKepler, Period, DMS2Rad, GMSTime,
TruEarth, DeltaQTarget, AttitudeTarget
------------------------------------------------------------------------

Setup the orbit
Constants
Ground target
Simulation parameters
Compute orbital elements and show ground track with target
Initial conditions for attitude dynamics
The plant: rigid body model
The controller
Calculate state-space control system matrices:
Simulation
plots
animation

%--------------------------------------------------------------------------
%   Copyright (c) 2008 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

Setup the orbit

%----------------

Constants

%--------------
Re = 6378.14; % radius of Earth (km)

Ground target

%--------------
tgt.latitude  = DMS2Rad( 51, 15, 44.20 ); % latitude to point at (rad)
tgt.longitude = DMS2Rad( -2, 17, 17.27 ); % longitude to point at (rad)
tgt.u         = [1;0;0];                  % body vector to point

Simulation parameters

%----------------------------
jD       = Date2JD+100;  % today's date in Julian date format
alt      = 400;      % altitude of orbit (km)
tSpan    = 3*60;     % time span to simulate (seconds)
tSamp    = 0.25;     % control sampling time (seconds)

Compute orbital elements and show ground track with target

%-----------------------------------------------------------
time  = 0:tSamp:tSpan;
T     = Period(Re+alt);                       % orbit period (sec)
gms   = GMSTime( jD )*pi/180;    % Greenwich mean time at jD (deg)
rA    = gms-pi/2+tgt.longitude;  % Right ascension (rad)
inc   = tgt.latitude;            % Inclination (rad)
n     = OrbRate( Re+alt );       % mean orbit rate (rad/s)
M     = pi/2 - tSpan/2*n;        % initial mean anomaly
el    = [Re+alt, inc, rA, 0, 0, M];    % orbital elements
t     = linspace(0,tSpan,30);
[r,v] = RVFromKepler( el, t );
lla   = zeros(size(r));
for i=1:length(t),
   lla(:,i) = CoordinateTransform('eci','llr',r(:,i),jD+t(i)/86400);
end
Map('Earth','2d')
plot(lla(2,:)*180/pi,lla(1,:)*180/pi,'y')
plot(tgt.longitude*180/pi,tgt.latitude*180/pi,'r.','markersize',20)

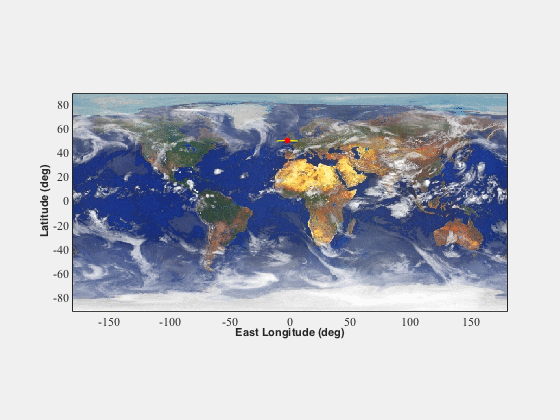
Initial conditions for attitude dynamics

q0          = [1;0;0;0];   % Initial ECI to Body quaternion
w0          = [0;0;0];     % Initial angular rates of Body [rad/sec]
inertia     = eye(3); % inertia matrix [kg-m^2]
noiseSigma  = 0;        % 1-sigma noise level for pointing knowledge [rad]

The plant: rigid body model

Our plant (the rigid body spacecraft) is a double integrator. The input to the the plant is a commanded angular acceleration. The output is an angular rotation.

Compute the plant statespace system

ap = [0 1;0 0]; bp = [0;1]; cp = [1 0]; dp = 0;

The controller

We will now design a PID controller with input "u" and output "y". It will have the following transfer function:

             Kr s         u
 y = Kp u +  ---- u + Ki ---
            s + wR        s

The gains (Kp, Kr, Ki) and the derivative roll-off term (wR) will be computed using the PIDMIMO function. It will compute these controller parameters so that the closed-loop system (the controlled spacecraft) will have the desired properties. We specify the desired properties in terms of: * natural frequency * damping ratio * integrator time constant * derivative roll-off frequency

zeta        = 0.7071;      % damping ratio (critically damped)
omega       = 0.3;         % natural frequency
tauInt      = 100;         % integrator time constant (sec)
omegaR      = 4;           % derivative roll-off
inr         = 1;           % unit inertia - controller outputs an acceleration
rateLimit   = .25;         % maximum angular rate [rad/s]
stepLimit   = rateLimit*tSamp;

Calculate state-space control system matrices:

[ak, bk, ck, dk, gains] = PIDMIMO( inr, zeta, omega, tauInt, omegaR);
[akd,bkd] = C2DelZOH(ak,bk,tSamp);
invInertia = inv(inertia);

Simulation

We will simulate a point mass orbit and a rigid body

xOrb = [r(:,1);v(:,1)];
xAtt = [q0;w0];

mu = Constant('mu earth');
orbitRHS = @(x,t) FOrbCart(x,t,0,mu);

d = struct;
d.qECIToBody = q0;
d.rECI = xOrb(1:3);
d.jD = jD;

xRoll = [0;0];
xPitch= [0;0];
xYaw  = [0;0];
xPlot = zeros(13,length(time));
trq   = zeros(3,length(time));
pointingError = zeros(1,length(time));
uTB           = zeros(3,length(time));
angleError    = trq;
qECIToTargetOld = q0;
for k = 1:length(time)
   xPlot(:,k) = [xAtt;xOrb]; % record
   qECIToBody = xAtt(1:4);   % rename for clarity

   % Compute the new target quaternion
   %----------------------------------
   d.qECIToBody = qECIToBody;
   d.rECI = xOrb(1:3);
   d.jD = jD+time(k)/86400;
   qTarget = AttitudeTarget( 'latlon', d, tgt );

   % Limit the total angular change
   %-------------------------------
   [qTargetToBody,qECIToTargetOld] = DeltaQTarget(qTarget,qECIToBody,...
                                                qECIToTargetOld,stepLimit);
   qBodyToTarget = QPose(qTargetToBody);

   qTToB = QMult( QPose(qTarget), qECIToBody );
   uTB(:,k) = QForm(qTToB,tgt.u);
   pointingError(k) = acos(dot(uTB(:,k),tgt.u));
   angleError(:,k) = 2*qBodyToTarget(2:4) + randn(3,1)*noiseSigma;

   % The delta form of the controller
   %---------------------------------
   acc    = zeros(3,1);
   acc(1) =          ck*xRoll   + dk*angleError(1,k);
   xRoll  = xRoll  + akd*xRoll  + bkd*angleError(1,k);
   acc(2) =          ck*xPitch  + dk*angleError(2,k);
   xPitch = xPitch + akd*xPitch + bkd*angleError(2,k);
   acc(3) =          ck*xYaw    + dk*angleError(3,k);
   xYaw   = xYaw   + akd*xYaw   + bkd*angleError(3,k);
   tExt  = -inertia*acc;

   % Numerical integration of the dynamics:
   xAtt = RK4( 'FRB', xAtt, tSamp, time(k), inertia, invInertia, tExt );
   xOrb = RK4( orbitRHS, xOrb, tSamp, time(k) );
   trq(:,k) = tExt;
end

plots

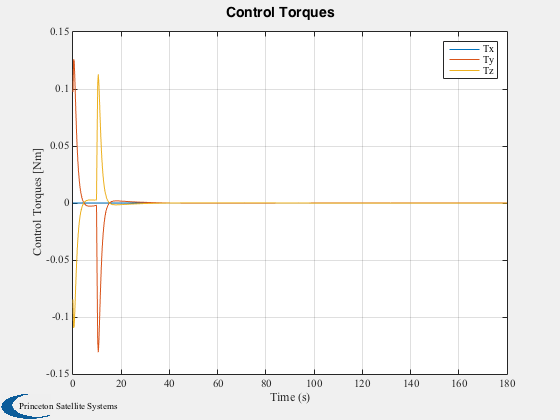
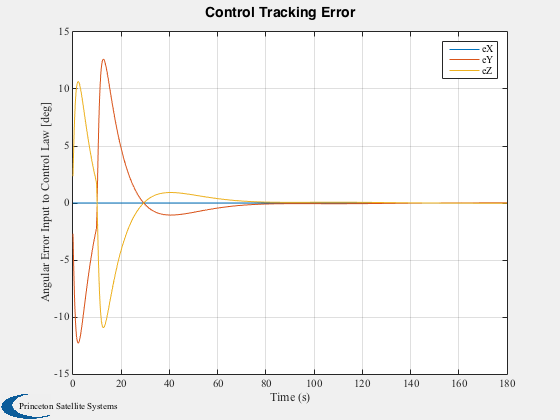
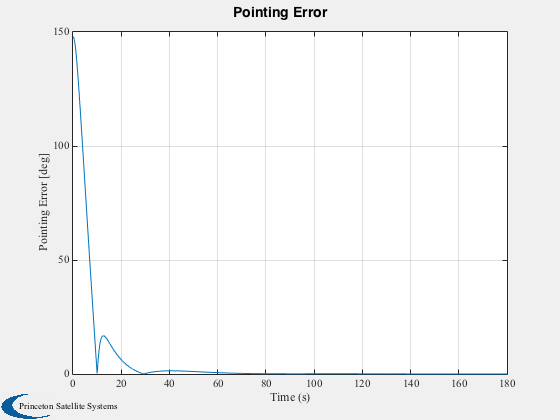
Plot2D(time,xPlot(1:4,:),'Time (s)','Quaternion','Inertial to Body Quaternion');
legend('qS','qX','qY','qZ');
Plot2D(time,xPlot(5:7,:)*180/pi,'Time (s)','Body rates [deg/s]','Body rates');
legend('wX','wY','wZ');
Plot2D(time,trq,'Time (s)','Control Torques [Nm]','Control Torques');
legend('Tx','Ty','Tz'),...
Plot2D(time,angleError*180/pi,'Time (s)','Angular Error Input to Control Law [deg]','Control Tracking Error');
legend('eX','eY','eZ');
Plot2D(time,pointingError*180/pi,'Time (s)','Pointing Error [deg]','Pointing Error');

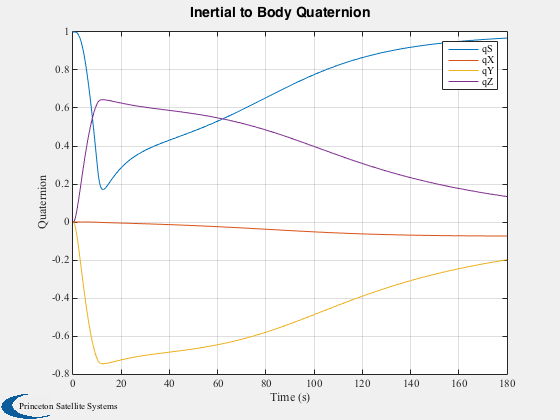
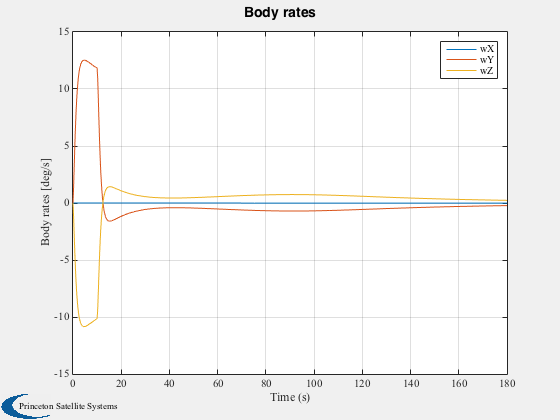
animation

animate the target vector in the Body frame during the transient period define end of transient period at point when pointing error drops below 1 deg

k = find( pointingError*180/pi > 1 );
AnimateVectors(uTB(:,1:k(end)),'y');


%--------------------------------------
% PSS internal file version information
%--------------------------------------