Controls the momentum in a spacecraft using solar pressure.

Uses a PI controller and a two degree of freedom gimbal at the end of the solar array. The solar pressure flap is a perfect mirror. The available torque is first mapped over a range of angles. Then a controller is designed and simulated. Note that the array can only provide torques in X and Z.

Since version 1.
--------------------------------------------------------------------------
See also SolarF., SunBeta, Mesh2, Normal, Plot2D, TimeLabl, Cross, SumV
-------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright 1996 Princeton Satellite Systems, Inc. All rights reserved.
%--------------------------------------------------------------------------

Constants

%----------
degToRad      = pi/180;
radToDeg      = 180/pi;
solarPressure = 1350/3e8;

The solar panel parameters in the inertial frame

%-------------------------------------------------
rCP   = [ 0.0  0.0;...
          5.0 -5.0;...
	        0.0  0.0 ];

area   = [0.5 0.5];
rho    = [0 0;1 1;0 0;0 0]; % All specular reflection (perfect mirrors)
normal = [0 0;0.7071 0.7071;0.7071 0.7071]; % This orientation gives us decoupled x and z torques

The nominal sun direction is +z

%--------------------------------
sunBeta = 0*degToRad;
uSun    = [0;-sin(sunBeta);cos(sunBeta)];

tX      = zeros(20,20);
tY      = zeros(20,20);
tZ      = zeros(20,20);

alpha   = (1:20) - 11;
beta    = (1:20) - 11;

Map out the control torques for +/- 10 degree rotations

%--------------------------------------------------------
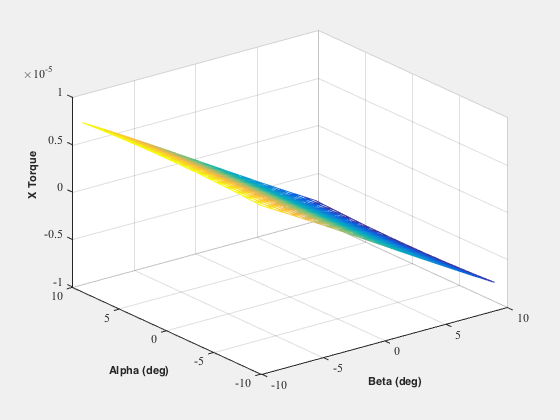
for i = 1:20
  for j = 1:20

    cA      = cos(alpha(i)*degToRad);
    sA      = sin(alpha(i)*degToRad);
    cB      = cos( beta(j)*degToRad);
    sB      = sin( beta(j)*degToRad);

    c1      = [cA 0  sA;0 1 0;-sA 0 cA]*[1 0 0;0 cB -sB;0  sB cB];
    c2      = [cA 0 -sA;0 1 0; sA 0 cA]*[1 0 0;0 cB  sB;0 -sB cB];

    normalI = [c1*normal(:,1),c2*normal(:,2)];
    f       = SolarF( solarPressure, rho, normalI, uSun, area );
    t       = SumV( Cross( rCP, f ) );
    tX(i,j) = t(1);
    tY(i,j) = t(2);
    tZ(i,j) = t(3);

  end
end

Mesh2(beta,alpha,tX,'Beta (deg)','Alpha (deg)','X Torque');
Mesh2(beta,alpha,tY,'Beta (deg)','Alpha (deg)','Y Torque');
Mesh2(beta,alpha,tZ,'Beta (deg)','Alpha (deg)','Z Torque');

Compute the forward gains in torque/rad

%----------------------------------------
kFX = (max(max(tX)) - min(min(tX)))/(( max(beta)- min(beta))*degToRad)
kFZ = (max(max(tZ)) - min(min(tZ)))/((max(alpha)-min(alpha))*degToRad)

kFX =

   4.6638e-05


kFZ =

   1.6082e-05

Simulate the control system

%----------------------------
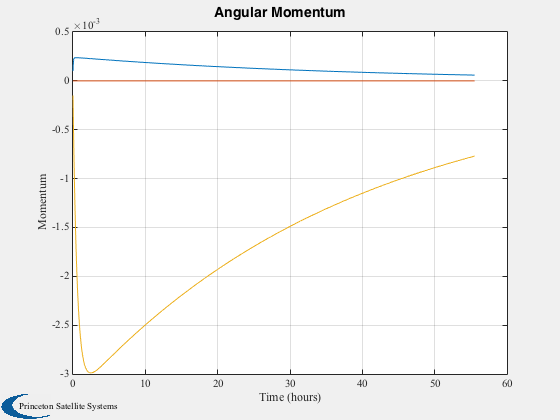
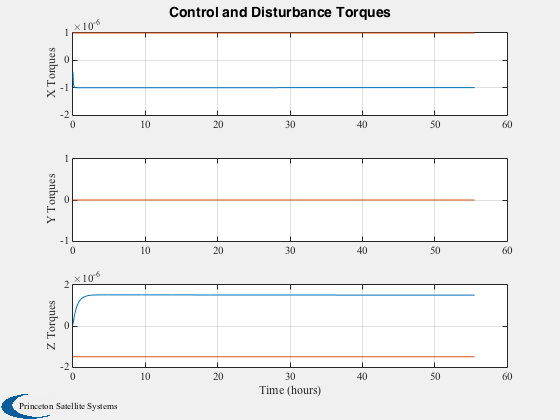
nSim   = 2000;
dT     = 100;
tD     = [1.e-6;0;-1.5e-6];   % disturbance torque
h      = [0.0001;0;-0.00015]; % initial angular momentum
hI     = [0;0;0];             % integral of momentum

Design the controller

%----------------------
w      = 0.001;
zeta   = 0.7071;
kM     = 2*zeta*w*[1/kFX;1/kFZ];
kI     = w^2*[1/kFX;1/kFZ];

Create the plotting arrays

%---------------------------
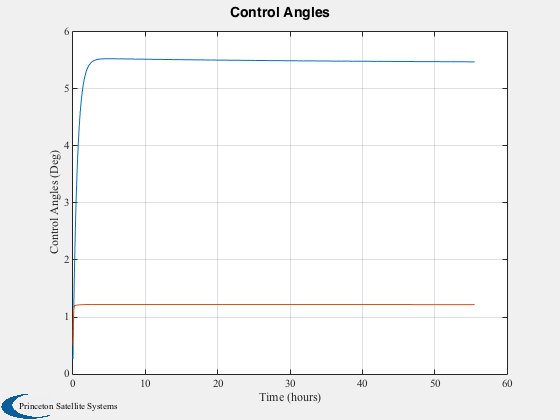
hPlot  = zeros(3,nSim);
tCPlot = zeros(3,nSim);
tDPlot = zeros(3,nSim);
aPlot  = zeros(2,nSim);

for k = 1:nSim
  hI          =  hI + h;
  alpha       = -(kM(1)*h(3) + kI(1)*hI(3));
  beta        =  (kM(2)*h(1) + kI(2)*hI(1));
  cA          =  cos(alpha);
  sA          =  sin(alpha);
  cB          =  cos( beta);
  sB          =  sin( beta);

  c1          =  [cA 0  sA;0 1 0;-sA 0 cA]*[1 0 0;0 cB -sB;0  sB cB];
  c2          =  [cA 0 -sA;0 1 0; sA 0 cA]*[1 0 0;0 cB  sB;0 -sB cB];

  normalI     =  [c1*normal(:,1),c2*normal(:,2)];
  f           =  SolarF( solarPressure, rho, normalI, uSun, area );
  t           =  SumV( Cross( rCP, f ) );
  hPlot(:,k)  =  h;
  tCPlot(:,k) =  t;
  tDPlot(:,k) =  tD;
  aPlot(:,k)  =  [alpha;beta]*radToDeg;
  h           =  h + dT*(tD + t);
end

time = dT*(0:(nSim-1));
[tPlot, tLbl] = TimeLabl( time );
Plot2D(tPlot, hPlot,tLbl,'Momentum','Angular Momentum');
Plot2D(tPlot, aPlot,tLbl,'Control Angles (Deg)','Control Angles');
yL = ['X Torques';'Y Torques';'Z Torques'];
Plot2D(tPlot,[tCPlot;tDPlot],tLbl,yL,'Control and Disturbance Torques','lin',['[1 4]';'[2 5]';'[3 6]']);


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b