Simulate a momentum bias spacecraft with a telescope on a roll pivot

The momentum wheel is used to control spacecraft pitch orientation.
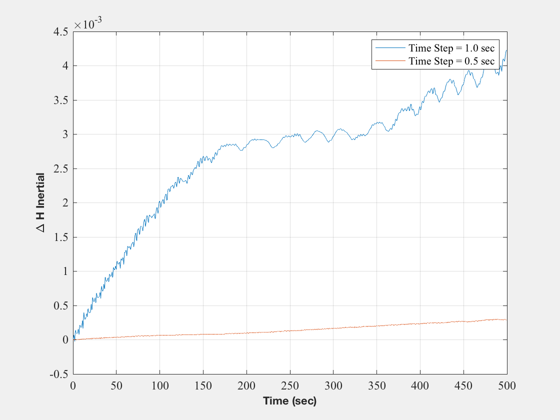
The script includes an initial test of angular momentum conservation.
It also computes the eigenvalues for the spacecraft when it is earth
pointing.

In the simulation the telescope points at a ground target.

%--------------------------------------------------------------------------
%  See also LatLonAltToEF, OmegaLVLH, QLVLH, EarthRot, RHSThreeBody,
%  NewFig, Plot2D, TimeLabl, XLabelS, YLabelS, Date2JD, JD2T, Jacobian, RK4,
%  Dot, Mag, Unit
% -------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2012 Princeton Satellite Systems, Inc.
%   All Rights Reserved.
%--------------------------------------------------------------------------
%   Since version 10.
%--------------------------------------------------------------------------

% Set the flag to test the angular momentum
%------------------------------------------
testAngularMomentum = 1;

d           = struct();

% Satellite properties
%---------------------
d.inr0      = diag([1 2 3]);
d.inr1      = diag([1 2 1]);
d.inr2      = diag([0.2 2 0.5]);
d.m0        = 1;
d.m1        = 0;
d.m2        = 0;
d.u1        = [1;0;0];
d.u2        = [1;0;0];
d.rho0      = [0;0;0];
d.rho1      = [0.0;0;0];
d.rho2      = [0;0;0];
d.lambda1	= [0;0;0];
d.lambda2	= [0;0;0];
d.torque0   = [0;0;0];
d.torque1   = 0;
d.torque2   = 0;

tEnd        = 60;
dTSim       = 0.1;
nSim        = ceil(tEnd/dTSim);

jD0         = Date2JD([2014 7 1 0 0 0]);

% Timesteps for testing the angular momentum
%-------------------------------------------
dT = [0.5 0.25];

if( testAngularMomentum )
  % Compute the angular momentum
  %-----------------------------
  n = 1000;

  % State [a;omega0;theta1;theta2;omega1;omega2]
  %---------------------------------------------
  x = [1;0;0;0;.1;0.2;0.3;0;0;0;0.0];
  h1 = zeros(1,n);
  for k = 1:n
    [nU,h] = RHSThreeBody(x,0,d);
    h1(k)	 = Mag(h);
    x      = RK4('RHSThreeBody',x,dT(1),0,d);
  end

  x = [1;0;0;0;.1;0.2;0.3;0;0;0;0.0];
  h2 = zeros(1,2*n);
  for k = 1:2*n
    [nU,h] = RHSThreeBody(x,0,d);
    h2(k)	 = Mag(h);
    x      = RK4('RHSThreeBody',x,dT(2),0,d);
  end

  t1 = (0:(n  -1))*dT(1);
  t2 = (0:(2*n-1))*dT(2);

  NewFig('|H|')
  plot(t1,h1-h1(1),t2,h2-h2(1));
  legend('Time Step = 1.0 sec','Time Step = 0.5 sec');
  XLabelS('Time (sec)')
  YLabelS('\Delta H Inertial')
  grid
end

% Run the simulation
%-------------------
mu	= 3.98600436e5;
r   = [6678.165;0;0];
v   = [0;sqrt(mu/r(1));0];
q   = QLVLH(r,v);
w   = OmegaLVLH(r,v);
x   = [q;w;0;0;0;0];

a   = Jacobian('RHSThreeBody',x,0,d);

fprintf(1,'Eigenvalues: Orbit rate = %12.4f rad/s',sqrt(mu/r(1)^2))
eig(a)

% Taywarah, Afghanistan
%----------------------
lat = 33.51987810*pi/180;
lon = 64.41708930*pi/180;
alt = 2.2; % km

rTarget = LatLonAltToEF([lat;lon;alt]);
rTarget = [6378.165;0;0];

xOrb    = [r;v];

t       = 0;
xP      = zeros(18,nSim);

for k = 1:nSim
  jD       = jD0 + t/86400;
  mEFToECI = EarthRot( JD2T(jD) );
  rECI     = mEFToECI*rTarget;
  angle    = acos(Dot(Unit(-rECI),Unit(xOrb(1:3)-rECI)))*180/pi;
  xP(:,k)	 = [x;xOrb;angle];
  xOrb     = RK4('FOrb', xOrb, dTSim, t, 'car');
  x        = RK4('RHSThreeBody',x,dTSim,0,d);
  t        = t + dTSim;
end

[t, tL] = TimeLabl((0:(nSim-1))*dTSim);
yL = {'q_s' 'q_x' 'q_y' 'q_z' '\omega_x' '\omega_y' '\omega_z' '\theta_1' '\theta_2' '\omega_1' '\omega_2', 'x (km)' 'y (km)' 'z (km)' 'Horizon Angle (deg)'};
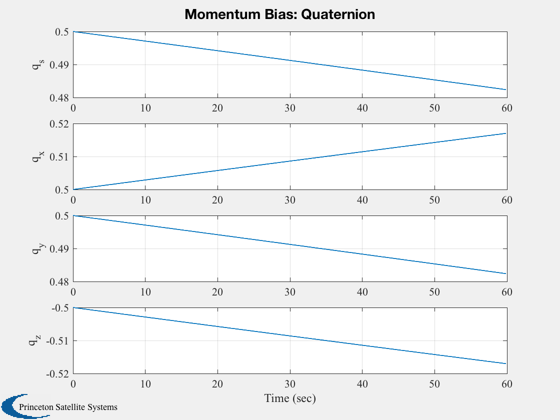
Plot2D(t,xP(  1:4,:),tL,yL( 1: 4),'Momentum Bias: Quaternion'   );
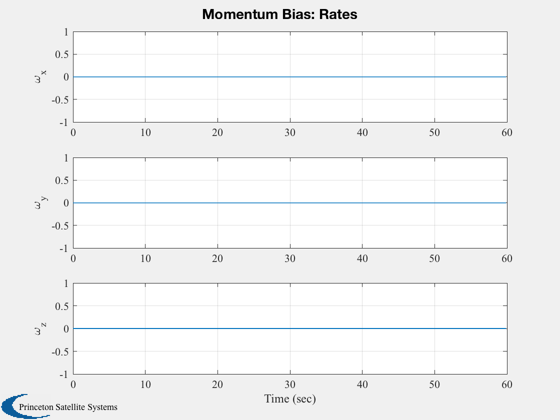
Plot2D(t,xP(  5:7,:),tL,yL( 5: 7),'Momentum Bias: Rates'        );
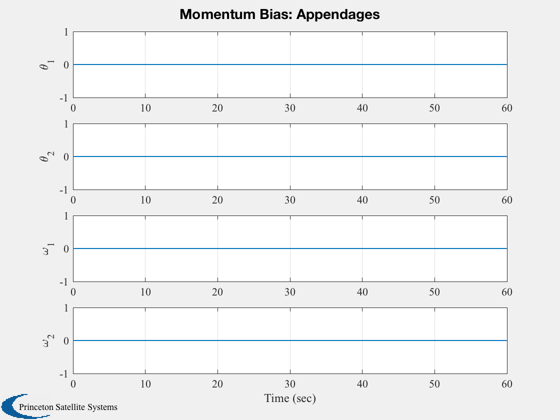
Plot2D(t,xP( 8:11,:),tL,yL( 8:11),'Momentum Bias: Appendages'   );
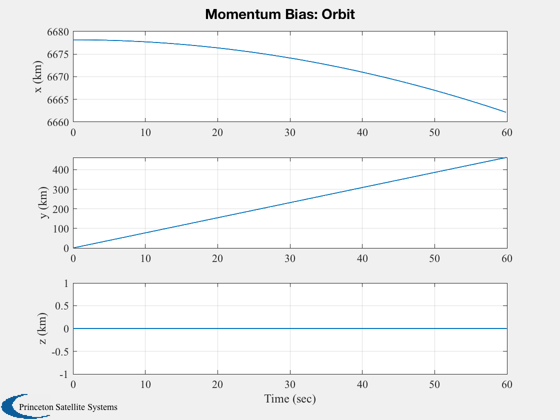
Plot2D(t,xP(12:14,:),tL,yL(12:14),'Momentum Bias: Orbit'        );
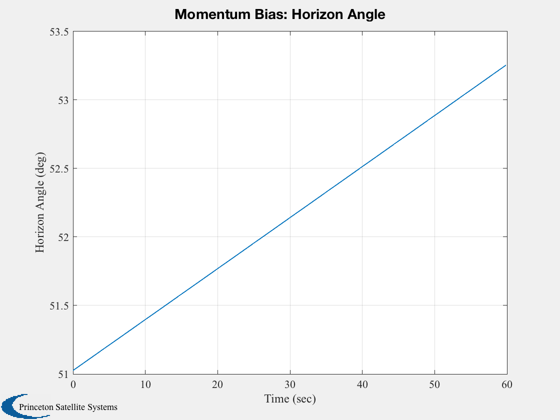
Plot2D(t,xP(   18,:),tL,yL(   15),'Momentum Bias: Horizon Angle');


%--------------------------------------

Eigenvalues: Orbit rate =       0.0945 rad/sans =
  0.000000000000000 + 0.000578433145908i
  0.000000000000000 - 0.000578433145908i
  0.000000000000000 + 0.000578433145908i
  0.000000000000000 - 0.000578433145908i
  0.002718246887781 + 0.000000000000000i
 -0.002718246887781 + 0.000000000000000i
  0.000000000000000 + 0.001156866291817i
  0.000000000000000 - 0.001156866291817i
 -0.000834826754860 + 0.000000000000000i
  0.000834826754860 + 0.000000000000000i
  0.000000000000000 + 0.000000000000000i

Published with MATLAB® R2019a