Attitude control of a sail using ballast masses in-plane.

Demonstrates control of a single axis using a simple PID controller.
This uses a fixed-rate dynamics model that is suitable for masses that
are controlled by stepper motors.

Demonstrates:
   PlateWithMasses
   PIDMIMO
   FMovingBody and FCoreAndMoving
   TorqueToCM
   CMToMassPositions

Since version 7.
------------------------------------------------------------------------
See also AC, PIDMIMO, QTForm, QZero, Plot2D, Cross, RK4,
CMToMassPositions, TorqueToCM, FCoreAndMoving, FMovingBody
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%   This file is referenced for listings in the User's Guide.
%-------------------------------------------------------------------------------

%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%  User Parameters
pitchStep = 0.01;  % y-axis, radians
yawStep   = 0.01;  % z-axis, radians
%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clear SailDisturbance

%---------------------------------------------------------

First, create suitable CAD model

%---------------------------------------------------------
g = load('PlateWithMasses');

%---------------------------------------------------------

Second, design controller

%---------------------------------------------------------

Control parameters - use PIDMIMO to design control loops

%---------------------------------------------------------
xN           = zeros(6,1);      % Controller state
iner         = diag([1 1 1]);   % Unit inertia
zeta         = 2;               % Damping ratio
wn           = 0.001;           % Control frequency
tauInt       = 5000;            % Integrator time constant
omegaR       = 5*wn;            % Rate filter frequency
sType        = 'z';             % Type of equations
dT           = 30;              % sec
% Resulting control values will be accelerations (due to unit inertia input).
[aC, bC, cC, dC] = PIDMIMO( iner, zeta*ones(1,3), wn*ones(1,3), tauInt*ones(1,3), ...
                            omegaR*ones(1,3), dT, sType );

uControl = [0 1 0; 0 0 1]';
dOffset  = zeros(3,3);
mControl = [g.body(1).mass.mass g.body(2).mass.mass g.body(3).mass.mass];

%---------------------------------------------------------

Third, set up an attitude maneuver to simulate

%---------------------------------------------------------

% States for each body, including attitude, are stacked
xCore = [zeros(6,1);QZero;zeros(3,1)];
xMass = [zeros(6,1);QZero;zeros(3,1)];
x     = [xCore; xMass; xMass];
iR1   = 2+13;  % y mass position
iR2   = 3+26;  % z mass position
iV1   = 5+13;  % y mass velocity
iV2   = 6+26;  % z mass velocity

% New attitude command
angCommand = [0;pitchStep;yawStep];

% Assume a contant sail force in the ECI frame
f        = struct;
f.total  = [-2*1367/3e8*100^2;0;0];
tq       = struct;
tq.total = [0;0;0];

% Assume center of pressure is at origin
Cp       = [0;0;0];

% Additional fields for RHS
d.g      = g;
d.nBody  = 3;
maxRate  = 1;  % m/s

%---------------------------------------------------------

Fourth, simulate maneuver

%---------------------------------------------------------

% Number of simulation points
nSim = 60;

% Preallocate plotting arrays
xPlot  = zeros(size(x,1),nSim);
tPlot  = zeros(1,nSim);
aEPlot = zeros(3,nSim);
TcPlot = zeros(3,nSim);
TaPlot = zeros(3,nSim);

% Simulation loop
for k = 1:nSim
  % Transverse angle error (small angles)
  angleError = [0;0;0];
  u = QTForm( x(7:10), [1;0;0] );
  angleError(3) = u(2) - angCommand(3);
  angleError(2) = -u(3) - angCommand(2);

  % Control
  yN = cC*xN + dC*angleError;
  xN = aC*xN + bC*angleError;
  Tcommand = -g.mass.inertia*yN;

  % Actuation
  cM         = TorqueToCM( Tcommand, f.total, Cp );
  rhoCommand = CMToMassPositions( cM, mControl, dOffset, uControl );
  rhoActual  = [x(iR1); x(iR2)];
  deltaRho   = rhoCommand - rhoActual;
  rhoDot     = sign(deltaRho).*min( abs(deltaRho)/dT, maxRate*[1;1] );

  % Update rates
  xRates = x;
  xRates(iV1) = rhoDot(1);
  xRates(iV2) = rhoDot(2);
  xNew = FMovingBody( 'init', x, xRates, tq, struct('g', g) );

  % Disturbances - simple torque model
  g.body(2).rHinge = [0;rhoActual(1);0];
  g.body(3).rHinge = [0;0;rhoActual(2)];
  cMActual = (mControl(2)*g.body(2).rHinge + mControl(3)*g.body(3).rHinge)/g.mass.mass;
  tq.total = Cross( Cp - cMActual, f.total );
  d.force  = f;
  d.torque = tq;

  % Store
  xPlot(:,k)  = x;
  tPlot(:,k)  = (k-1)*dT;
  aEPlot(:,k) = angleError;
  TcPlot(:,k) = Tcommand;
  TaPlot(:,k) = tq.total;

  % Integrate
  x = RK4( @FCoreAndMoving, xNew, dT, 0, '', d );
end

%---------------------------------------------------------

Plot

%---------------------------------------------------------
h = [];
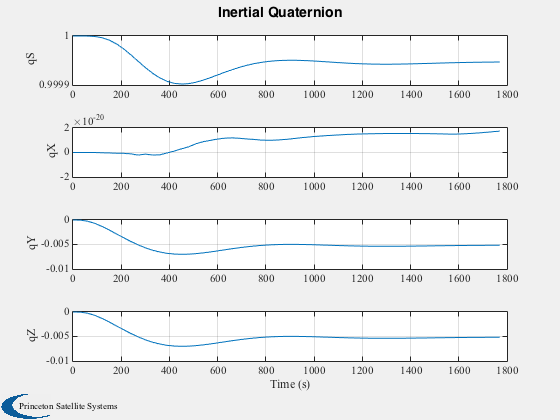
h(1) = Plot2D( tPlot, xPlot(7:10,:), 'Time (s)', {'qS','qX','qY','qZ'},'Inertial Quaternion' );
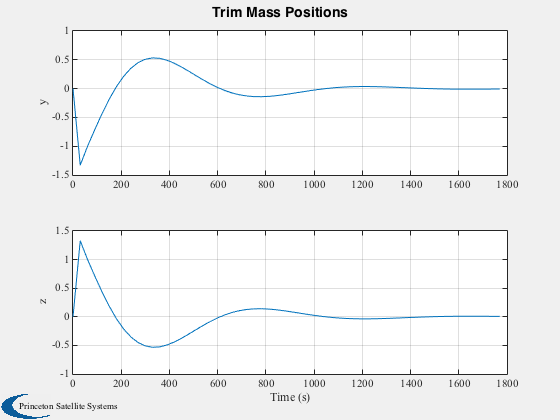
h(2) = Plot2D( tPlot, xPlot([iR1 iR2],:), 'Time (s)', {'y','z'},'Trim Mass Positions' );
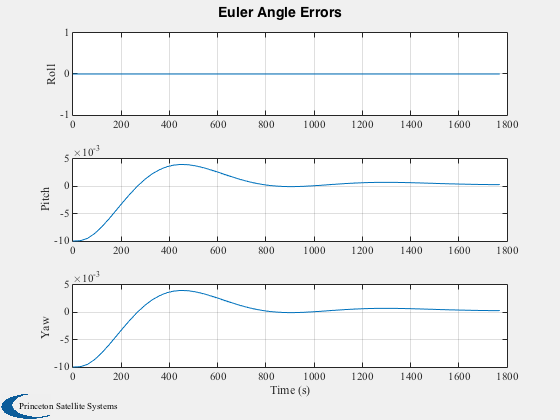
h(3) = Plot2D( tPlot, aEPlot, 'Time (s)', {'Roll','Pitch','Yaw'},'Euler Angle Errors' );
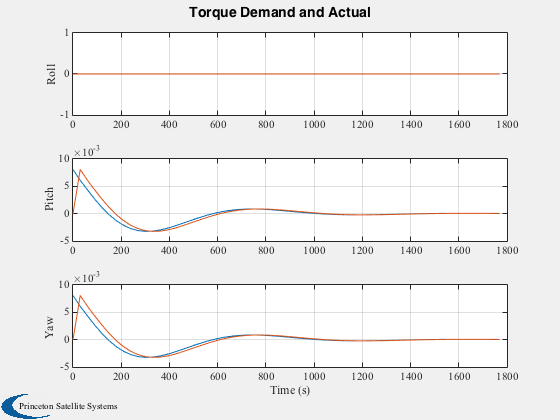
Plot2D( tPlot, [TcPlot;TaPlot], 'Time (s)', {'Roll','Pitch','Yaw'},'Torque Demand and Actual',...
  'lin',{[1 4],[2 5],[3 6]});

if 0
  % print figures for User's Guide.
  figure(h(3));
  print -depsc2 AngleErrorsM1Axis
  figure(h(2));
  print -depsc2 MassPositionsM1Axis
  figure(h(1));
  print -depsc2 QInertialM1Axis
end


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b