Attitude control of a sail using control vanes.

The attitude dynamics are rigid body. The vanes are assumed to reach
the commanded location instanteously and inertia effects are neglected.

Functions demonstrated:
     PlateWithVanes
     PIDMIMO
     SailDisturbance
     FRB
     VaneAngles

Since version 7.
------------------------------------------------------------------------
See also AC, PIDMIMO, Eul2Q, Q2Eul, QMult, QPose, QZero, Constant,
Plot2D, RK4, Unit, JD2000, El2RV, FRB, VaneAngles, QSail,
DisturbanceStruct, EnvironmentStruct, ProfileStruct, SailDisturbance,
SailEnvironment
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%   This file is referenced for listings in the User's Guide.
%-------------------------------------------------------------------------------

%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%  User Parameters
rollStep = 0.01;  % radians
specular = 1;     % use ideal specular properties for sail and vanes
pitch    = 0;     % initialize sail with nonzero pitch angle (sun angle)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clear SailDisturbance

%---------------------------------------------------------

First, create suitable CAD model.

%---------------------------------------------------------
% The sail is 100 m square.
g = load('PlateWithVanes');
lSail = 100;

if ~specular
  % overwrite sail and vane optical properties with nonideal values
  optical = g.component(2).optical;
  optical.sigmaS = 0.9;
  optical.sigmaA = 0.08;
  optical.sigmaD = 0.02;
  for k = 1:3
    g.component(k+1).optical = optical;
  end
end

%---------------------------------------------------------

Second, design controller

%---------------------------------------------------------

% Control parameters - use PIDMIMO to design control loops
xN           = zeros(2,1);      % Controller state
iner         = 1;               % Unit inertia
zeta         = 2;               % Damping ratio
wn           = 0.001;           % Control frequency
tauInt       = 3000;            % Integrator time constant
omegaR       = 5*wn;            % Rate filter frequency
sType        = 'z';             % Type of equations
dT           = 50;
% Resulting control values will be accelerations (due to unit inertia input).
[aC, bC, cC, dC] = PIDMIMO( iner, zeta, wn, tauInt, omegaR, dT, sType );

% Actuator model, assume sail is 100 m and vane is 5%
areaVane = 0.05*lSail^2;
lBoom    = lSail/sqrt(2);
Ps       = 1367/Constant('speed of light')/1000;

%---------------------------------------------------------

Third, set up an attitude maneuver to simulate

%---------------------------------------------------------

% Need an epoch and orbit state to use full disturbance model
[r,v] = El2RV( [Constant('au') 0 0 0 0 0], [], Constant('mu sun') );
jD    = JD2000;
qS    = QSail( -Unit(r), r, v );
if pitch
  qY = Eul2Q([0;5*pi/180;30*pi/180]);
else
  qY = QZero;
end
q0    = QMult(qS,qY);

% for integration will just use attitude states
x     = [q0;zeros(3,1)];

% New attitude command - step around roll
rollCommand = rollStep;

% Environment and disturbance models
d = struct;
d = EnvironmentStruct( d );
d = DisturbanceStruct( d );
d.aeroOn   = 0;
d.albedoOn = 0;
d.magOn    = 0;
d.radOn    = 0;

% Profile
p    = ProfileStruct;
p.q  = qS;
p.r  = r;
p.v  = v;
p.jD = jD;
% states for rotating vanes
p.body  = [2 3];
p.angle = [0; 0];
p.axis  = [0 0 1; 0 0 1]';

% Environment will be constant over this short period
env = SailEnvironment( 'sun', p, d );

% inertia and inverse for rigid body model
inr    = g.mass.inertia;
invInr = inv(inr);

%---------------------------------------------------------

Fourth, simulate maneuver

%---------------------------------------------------------

% Number of simulation points
nSim = 100;

% Preallocate plotting arrays
xPlot  = zeros(size(x,1),nSim);
tPlot  = zeros(1,nSim);
aEPlot = zeros(1,nSim);
thPlot = zeros(1,nSim);
tqPlot = zeros(3,nSim);

% Simulation loop
for k = 1:nSim
  % Euler angle error (small angles)
  qSB        = QMult( QPose( qS ), x(1:4) );
  eulActual  = Q2Eul(qSB);
  angleError = eulActual(1) - rollCommand;

  % Control
  yN = cC*xN + dC*angleError;
  xN = aC*xN + bC*angleError;
  Tcommand = -g.mass.inertia(1,1)*yN;

  % Actuation - vane angle
  p.angle  = VaneAngles( areaVane*cos(25*pi/180)*[1; 1], lBoom, Tcommand );

  % Disturbances
  [f, tq] = SailDisturbance( g, p, env, d );

  % Store
  xPlot(:,k)  = x;
  tPlot(:,k)  = (k-1)*dT;
  aEPlot(:,k) = angleError;
  thPlot(:,k) = p.angle(1);
  tqPlot(:,k) = tq.total;

  % Integrate
  x = RK4( @FRB, x, dT, 0, inr, invInr, tq.total );
end

%---------------------------------------------------------

Plot

%---------------------------------------------------------
h = [];
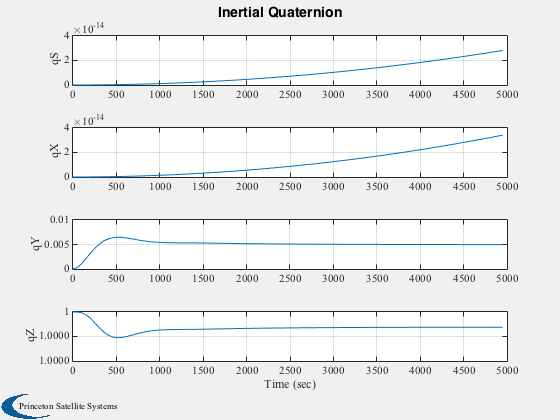
h(1) = Plot2D( tPlot, xPlot(1:4,:), 'Time (sec)', {'qS','qX','qY','qZ'},'Inertial Quaternion' );
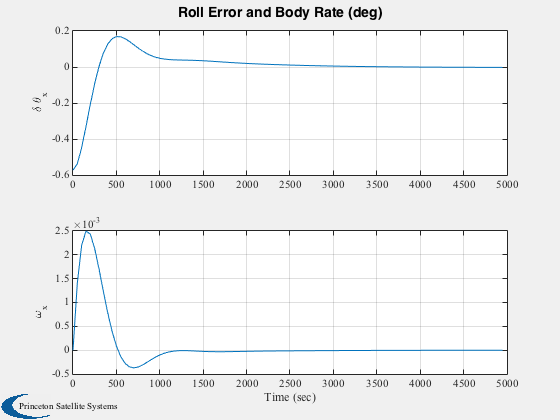
h(2) = Plot2D( tPlot, [aEPlot;xPlot(5,:)]*180/pi, 'Time (sec)', {'\delta \theta_x','\omega_x'},...
               'Roll Error and Body Rate (deg)' );
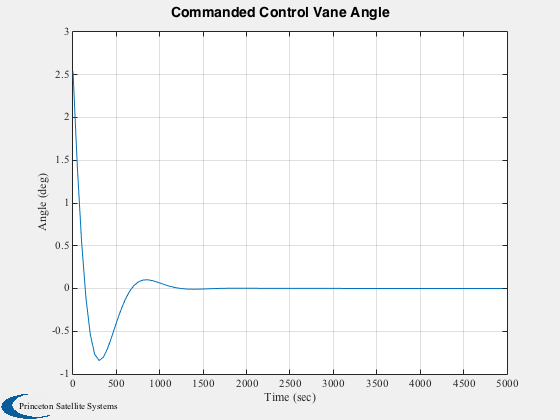
h(3) = Plot2D( tPlot, thPlot*180/pi, 'Time (sec)', 'Angle (deg)', 'Commanded Control Vane Angle' );
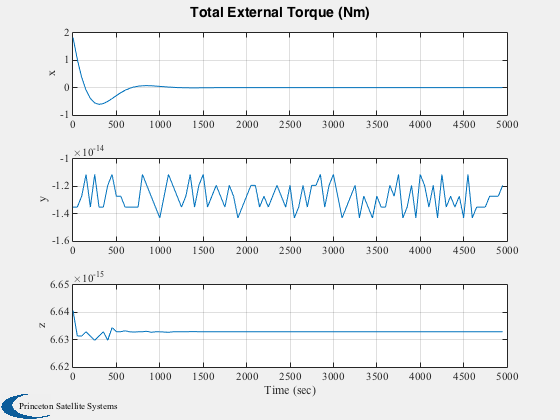
Plot2D( tPlot, tqPlot*180/pi, 'Time (sec)', {'x','y','z'}, 'Total External Torque (Nm)' );

if 0
  % print figures for User's Guide.
  figure(h(3));
  print -depsc2 VaneAngleV1Axis
  figure(h(2));
  print -depsc2 RollErrorsV1Axis
  figure(h(1));
  print -depsc2 QInertialV1Axis
end


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b