Earth-orbit sail analysis with sail aligned to LVLH.

The sail is in a dawn-dusk sun-synchronous orbit. The sail tracks the LVLH frame with fixed "yaw" offsets (rotation about the nadir vector). This script demonstrates the difference between sail angle definitions for a planet-centric orbit. Note in the last plot that the cone and clock angles for a fixed yaw offset are not constant due to the orbit geometry of the selected date.

Since version 7.
------------------------------------------------------------------------
See also: SunV2, UToConeClock, ClockConversion, Eul2Q, QForm, QLVLH,
QMult, QPose, QTForm, Plot2D, TimeLabl, Unit, Date2JD, JDToDateString,
RVOrbGen, El2RV, PltOrbit, VOrbit, VisualizeSailAttitude
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 2006,2009 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

Orbit and epoch

%----------------
el        = [7978.1;1.7891;1.5708;3.0220;0;0];
jD0       = Date2JD([2010 3 15, 16 0 0]);
[r,v]     = El2RV( el );
uSun      = SunV2( jD0 );

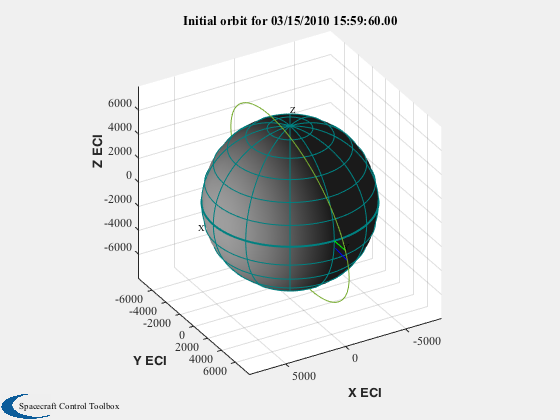
Draw orbit

%-----------
PltOrbit( el, jD0 )
hold on;
plot3(r(1),r(2),r(3),'*')
title(['Initial orbit for ' JDToDateString(jD0)])

ans = 
  Figure (PlotPSS) with properties:

      Number: 2
        Name: 'Earth Orbit'
       Color: [0.94 0.94 0.94]
    Position: [440 378 560 420]
       Units: 'pixels'

  Use GET to show all properties

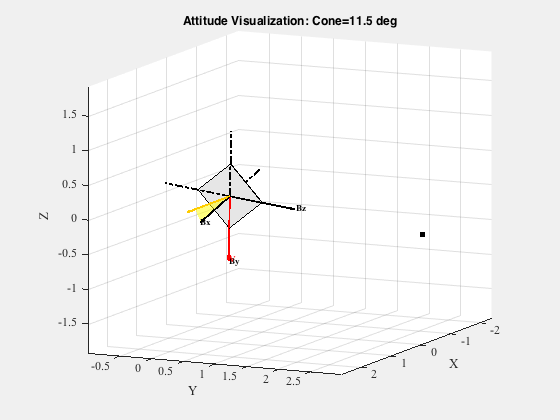
Attitude

%---------
% PSS LVLH frame: z is in the -r direction, y is in the - rxv direction,
% and x completes the set.
% Nominal sail orientation: body z aligned with LVLH x, body x along orbit normal
% --> -90* rotation about z axis
qLVLH = QLVLH( r, v );
qLVLHToBody = Eul2Q([0;0;-pi/2]);
q0 = QMult( qLVLH, qLVLHToBody );
VisualizeSailAttitude( q0, uSun )
% Add earth
hold on;
rE = QTForm( qLVLH, [0;0;3] );
plot3([rE(1)],[rE(2)],[rE(3)],'k.','markersize',20)
vhat = Unit(v);
qV = quiver3(0,0,0,vhat(1),vhat(2),vhat(3),0);
set(qV,'color','r','linewidth',2)
tt = text(vhat(1),vhat(2),vhat(3),'V')
set(tt,'fontweight','bold','color','r')
view(115,10)

ans =
      0.20005
tt = 
  Text (V) with properties:

                 String: 'V'
               FontSize: 9
             FontWeight: 'normal'
               FontName: 'Times'
                  Color: [0 0 0]
    HorizontalAlignment: 'left'
               Position: [-0.21503 -0.11931 -0.96929]
                  Units: 'data'

  Use GET to show all properties

Propagate for one orbit and plot cone/clock angles

%---------------------------------------------------
[rOrbit,vOrbit,tPlot] = RVOrbGen(el);
[tPlot,tLabl] = TimeLabl(tPlot);
qLVLH = QLVLH( rOrbit, vOrbit );
sVec  = repmat(uSun,1,size(qLVLH,2));
dCC   = struct('r',rOrbit,'v',vOrbit,'s',sVec,'c',1);

for k = 1:size(qLVLH,2)
  qOrbit(:,k) = QMult( qLVLH(:,k), qLVLHToBody );
end

Sail normal vector is body X axis

%----------------------------------
nHat = QTForm( qOrbit, [1;0;0] );

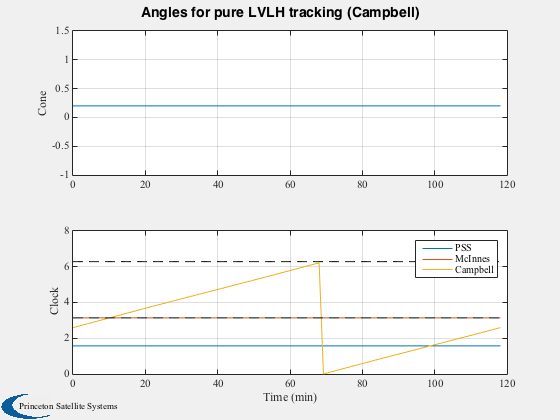
Cone and clock measured from Earth orbit/pure LVLH

%---------------------------------------------------
% Assume for a single orbit that the sun is fixed
[cone, clock]   = UToConeClock( nHat, rOrbit, vOrbit, sVec );
clockNew        = ClockConversion( cone, clock, 2, 1, dCC );
[cone3, clock3] = UToConeClock( -nHat, [], vOrbit, sVec, -1 );
Plot2D(tPlot,[cone;clock;clockNew;clock3],tLabl,{'Cone','Clock'},...
  'Angles for pure LVLH tracking (Campbell)',...
  [],{1,[2 3 4]});
legend('PSS','McInnes','Campbell')
hold on
plot(tPlot,pi*ones(size(tPlot)),'k--')
plot(tPlot,2*pi*ones(size(tPlot)),'k--')

% Result: cone angle is constant!

kN =
  Columns 1 through 13
     1     3     5     6     7     9    11    15    17    21    22    41    78
  Columns 14 through 25
    82    86    88    89    92    93    94    95    96    97    98   100

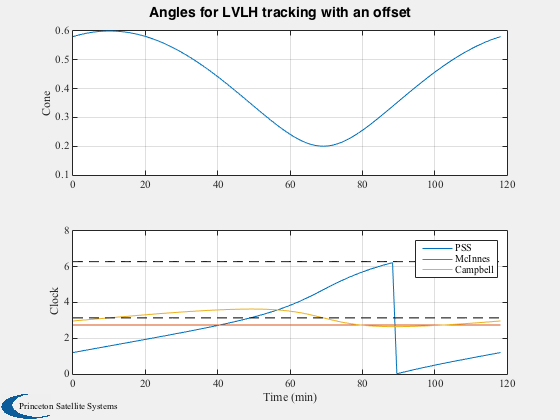
Now add fixed yaw angle to LVLH attitude

%-----------------------------------------
qYaw = Eul2Q([0;0;0.4]);
for k = 1:size(qLVLH,2)
  qECIYaw(:,k) = QMult( qOrbit(:,k), qYaw );
end
nHat = QForm( QPose(qECIYaw), [1;0;0] );
[cone, clock] = UToConeClock( nHat, rOrbit, vOrbit, sVec );
clockNew = ClockConversion( cone, clock, 2, 1, dCC );
[cone3, clock3] = UToConeClock( -nHat, [], vOrbit, sVec, -1 );
Plot2D(tPlot,[cone;clock;clockNew;clock3],tLabl,{'Cone','Clock'},...
  'Angles for LVLH tracking with an offset',...
  [],{1,[2 3 4]});
legend('PSS','McInnes','Campbell')
hold on
plot(tPlot,pi*ones(size(tPlot)),'k--')
plot(tPlot,2*pi*ones(size(tPlot)),'k--')

% Result: cone angle is NOT constant!

%--------------------------------------
% PSS internal file version information
%--------------------------------------

kN =
   Empty matrix: 1-by-0

Published with MATLAB® R2014b