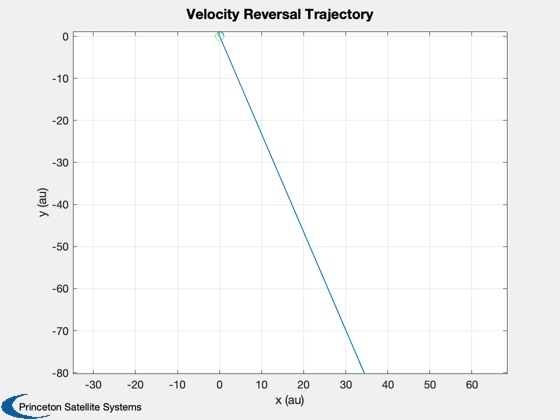
Planar heliopause mission simulation.

Can use either a built-in specular sail force disturbance function or the
full sail disturbance function. Uses the FlatSail CAD model.
The sail characteristic acceleration is about 4.6e-6 km/s2.

Functions demonstrated:
    RHSHelio2DOrbit
    HeliopauseSailAngle
    FlatPlate

Since version 7.
------------------------------------------------------------------------
See also Constant, Plot2D, TimeLabl, JD2000, HeliopauseSailAngle
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%	Copyright (c) 2005,2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% User Parameters
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Two choices of disturbance model:
%    1 (specular)
%    2 (full)
disturbModel = 1;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Load the flat plate model

%--------------------------
d.g = load(fullfile('SailData','FlatSail.mat'));


% Scale the sail
%---------------
d.g.component(1).v = 2*d.g.component(1).v;

Disturbance model data

%-----------------------
d.distModel.aeroOn   = 0;
d.distModel.albedoOn = 0;
d.distModel.solarOn  = 1;
d.distModel.magOn    = 0;
d.distModel.radOn    = 0;
d.distModel.ggOn     = 0;
d.distModel.planet   = 'Sun';
d.jD0                = JD2000;

The maximum number of days for the numerical integration

%---------------------------------------------------------
maxDays        = 365;

Constants

%----------
mu             = Constant('mu sun');
aU             = Constant('au'); % km
lbFToN         = Constant('lb force to n');
lbFToKg        = Constant('lb force to kg');
c              = Constant('speed of light')*1e3;
secInDay       = 86400;
mToKm          = 1/1000;

Build the data structure for the differential equations

%--------------------------------------------------------
d.tEnd         = maxDays*secInDay;
d.mu           = mu;
d.m0           = 100; % kg
d.laserOn      = 0;

The following are for the specular model only

%----------------------------------------------
area           = 350*d.m0;
p              = 1367;  % W/m2
d.accel        = 2.0*(p/c)*area*mToKm*aU^2/d.m0;

Sail pointing angle function

%-----------------------------
d.sailAngleFun = 'HeliopauseSailAngle';

Select the disturance model

%----------------------------
switch disturbModel
  case 1
    % This uses the specular model
    d.forceModel   = 'specular';
  otherwise
    % This uses the full disturbance model
    d.forceModel   = 'full';
end
disp('HeliopauseSimulation:')
disp(['Disturbance type: ' d.forceModel])

HeliopauseSimulation:
Disturbance type: specular

Set up ode113

%--------------
oDEOptions     = odeset( 'abstol', 1e-12, 'reltol', 4e-8, 'events', 'off' );

Initial conditions. States are [r;dr/dt;drTheta/dt]

%----------------------------------------------------
x              = [aU;0;sqrt(d.mu/aU);0];

[t, x]         = ode23('RHSHelio2DOrbit', [0, d.tEnd], x, oDEOptions, d );

x              = x';
angle          = HeliopauseSailAngle( x, t );
[t, tL]        = TimeLabl( t' );

Plot the orbit

%---------------
cA = cos( x(4,:) );
sA = sin( x(4,:) );
Plot2D( x(1,:).*cA/aU, x(1,:).*sA/aU, ['x (au)'], ['y (au)'],'Velocity Reversal Trajectory' )
hold on

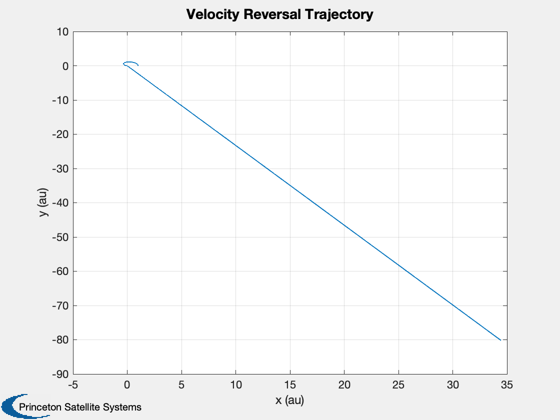
Plot the initial orbit

%-----------------------
th = linspace(0,2*pi);
plot(x(1,1)*cos(th)/aU,x(1,1)*sin(th)/aU,'g');
axis equal
hold off

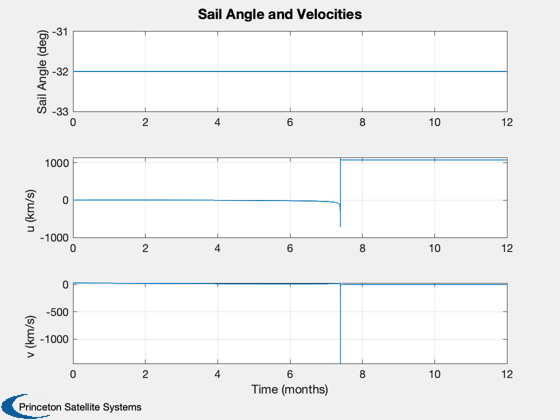
yL = {'Sail Angle (deg)' 'u (km/s)' 'v (km/s)'};
Plot2D( t, [angle*180/pi;x(2,:);x(3,:)], tL, yL, 'Sail Angle and Velocities' );


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2020a