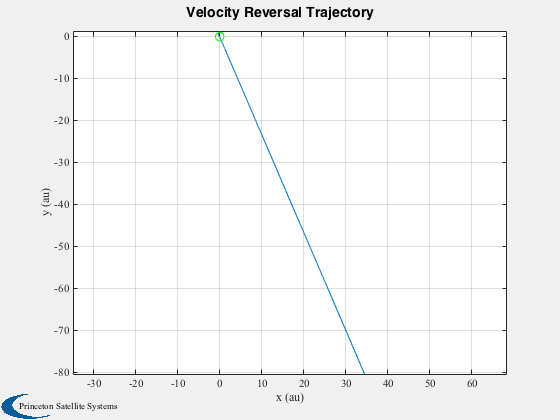
Planar heliopause mission simulation.

Can use either a built-in specular sail force disturbance function or the
full sail disturbance function. Uses the FlatSail CAD model.
The sail characteristic acceleration is about 4.6e-6 km/s2.

This simulation has a simple laser model. When the spacecraft is
past earth orbit it adds the power from the laser model along the
velocity vector. This is added to the sun acceleration. The laser model
only works with the specular model. The logic works by turning on the
laser after the spacecraft has flown by the sun.

Functions demonstrated:
    RHSHelio2DOrbit
    HeliopauseSailAngle
    FlatPlate

Since version 10.
------------------------------------------------------------------------
See also Constant, Plot2D, TimeLabl, JD2000, HeliopauseSailAngle
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%	Copyright (c) 2005,2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% User Parameters
%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Two choices of disturbance model:
%    1 (specular)
%    2 (full)
disturbModel = 1;
laserOn      = 0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Load the flat plate model

%--------------------------
d.g = load(fullfile('SailData','FlatSail.mat'));

% Scale the sail
%---------------
d.g.component(1).v = 2*d.g.component(1).v;

Disturbance model data

%-----------------------
d.distModel.aeroOn   = 0;
d.distModel.albedoOn = 0;
d.distModel.solarOn  = 1;
d.distModel.magOn    = 0;
d.distModel.radOn    = 0;
d.distModel.ggOn     = 0;
d.distModel.planet   = 'Sun';
d.jD0                = JD2000;

The maximum number of days for the numerical integration

%---------------------------------------------------------
maxDays        = 365;

Constants

%----------
mu             = Constant('mu sun');
aU             = Constant('au'); % km
lbFToN         = Constant('lb force to n');
lbFToKg        = Constant('lb force to kg');
c              = Constant('speed of light')*1e3;
secInDay       = 86400;
mToKm          = 1/1000;

Build the data structure for the differential equations

%--------------------------------------------------------
d.tEnd         = maxDays*secInDay;
d.mu           = mu;
d.m0           = 100; % kg

The following are for the specular model only

%----------------------------------------------
area           = 350*d.m0;
p              = 1367;  % W/m2
d.accel        = 2.0*(p/c)*area*mToKm*aU^2/d.m0;

Sail pointing angle function

%-----------------------------
d.sailAngleFun = 'HeliopauseSailAngle';

Select the disturance model

%----------------------------
switch disturbModel
  case 1
    % This uses the specular model
    d.forceModel   = 'specular';
  otherwise
    % This uses the full disturbance model
    d.forceModel   = 'full';
end
disp('HeliopauseSimulation:')
disp(['Disturbance type: ' d.forceModel])
if( laserOn == 1)
    disp('Laser on');
end

% This only works with the specular simulation
%---------------------------------------------
if( laserOn )
    d.laserOn        = 1;
    d.laser.power    = 1e9; % 10 GW
    d.laser.lambda   = 526e-9;
    d.laser.aperture = 10;
    d.laser.f        = 2.0*(1/c)*mToKm/d.m0;
    d.laser.area     = area;
    d.laser.aU       = aU;
else
    d.laserOn        = 0;
end

HeliopauseSimulation:
Disturbance type: specular

Set up ode113

%--------------
oDEOptions     = odeset( 'abstol', 1e-12, 'reltol', 4e-8, 'events', 'off' );

Initial conditions. States are [r;dr/dt;drTheta/dt]

%----------------------------------------------------
x              = [aU;0;sqrt(d.mu/aU);0];

[t, x]         = ode23('RHSHelio2DOrbit', [0, d.tEnd], x, oDEOptions, d );

x              = x';
angle          = HeliopauseSailAngle( x, t );
[t, tL]        = TimeLabl( t' );

Plot the orbit

%---------------
c              = cos( x(4,:) );
s              = sin( x(4,:) );
Plot2D( x(1,:).*c/aU, x(1,:).*s/aU, 'x (au)', 'y (au)','Velocity Reversal Trajectory' )
hold on

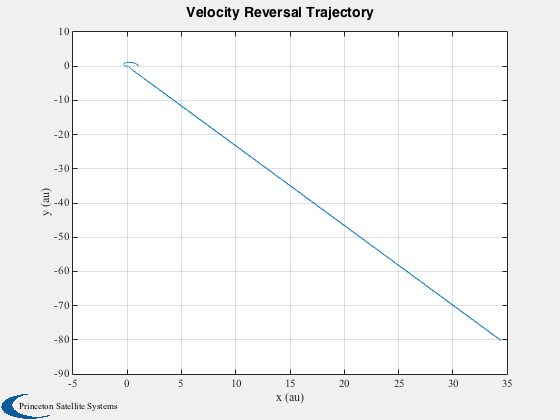
Plot the initial orbit

%-----------------------
a = linspace(0,2*pi);
plot(x(1,1)*cos(a)/aU,x(1,1)*sin(a)/aU,'g');
axis equal
hold off

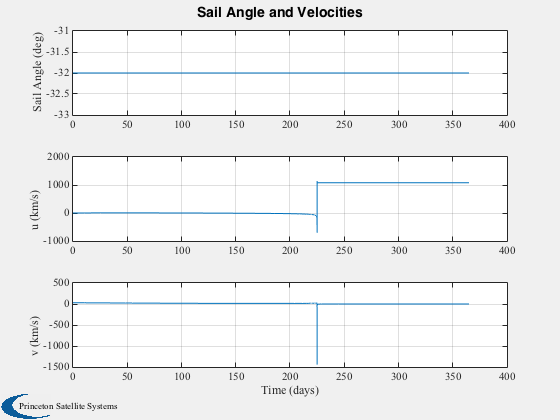
yL = {'Sail Angle (deg)' 'u (km/s)' 'v (km/s)'};
Plot2D( t, [angle*180/pi;x(2,:);x(3,:)], tL, yL, 'Sail Angle and Velocities' );


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b