Combined guidance and control demo with fixed rate two-body dynamics.

This script uses FMovingBody which distributes rates to the core body when
the boom is moved to conserve momentum.

This demo uses the PlateWithBoom CAD model. The control law is
designed using PIDMIMO. There is no roll actuation and therefore the
attitude trajectory must use only Y and Z torques.

The attitude dynamics assume fixed gimbal rates.
The CAD model is a perfectly specular plate with a control boom.
The time step is 600 sec for the outer ACS loop and 120 sec for the inner
loop which moves the boom.

Functions demonstrated:
    PIDMIMO
    QToConeClock
    FMovingBody
    SailDisturbance
    PlateWithBoom

Since version 7.
------------------------------------------------------------------------
See also AC, CrossSection, PIDMIMO, Q2AU, QForm, QTForm, QZero, U2Q,
Constant, WaitBarManager, Plot2D, Plot3D, TimeLabl, Cross, Mag, RK4, Unit,
JD2000, RV2AE, El2RV, Accel, FMovingBody, ClockConversion, ConeClockToU,
QToConeClock, FHingeOrbit, ProfileStruct, SailDisturbance,
SailEnvironment, delta, LocallyOptimalTraj
------------------------------------------------------------------------

Load the control boom sail model
Sim timing
Control parameters - use PIDMIMO to design attitude control loop
Sail physical parameters
Create the disturbance profile
Initial Julian date
We are creating a circular heliocentric orbit.
Orbit state
Initial Quaternion (inertial to body frame)
Create the data structure
Orbiting the sun.
Initial state
Simulation loop
Prepare data for plotting
Create Plots

%-------------------------------------------------------------------------------
%	  Copyright (c) 2005,2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%   This file is referenced for listings in the User's Guide.
%-------------------------------------------------------------------------------

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% User Parameters
%%%%%%%%%%%%%%%%%%
% Change these to explore the system dynamics.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Nominal gimbal rate (rad/s)
aRateNom = 0.3;
% Controller natural frequency (rad/sec)
wn = 0.0001;
% Duration for sim (days)
days = 2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clear SailDisturbance

%---------------------------------

Load the control boom sail model

%---------------------------------
g = load('PlateWithBoom.mat');
% To view the model, run: DrawSCPlanPlugIn( 'initialize', g );

Sim timing

%-----------
dTg  = 2*3600; % guidance update time
dTo  = 600;    % outer attitude dT
dTi  = dTo/5;  % inner dT
tDuration = days*86400;
nSim      = floor(tDuration/dTi);

%-----------------------------------------------------------------

Control parameters - use PIDMIMO to design attitude control loop

%-----------------------------------------------------------------
xN           = zeros(6,1);       % Controller state
iner         = diag([1 1 1]);    % Unit inertia
zeta         = 2;                % Damping ratio
omegaR       = 5*wn;             % Rate filter frequency
tauInt       = 10000;            % Integrator time constant
sType        = 'z';              % Type of equations
% Resulting control values are accelerations (due to unit inertia input).
[aC, bC, cC, dC] = PIDMIMO( iner, zeta*ones(1,3), wn*ones(1,3), tauInt*ones(1,3), ...
                            omegaR*ones(1,3), dTo, sType );

Sail physical parameters

%-------------------------
aSail = CrossSection(g);
fSail = 1367/3e8*2*aSail*[-1;0;0]; % Specular reflective force, N
aBoom(:,1) = Cross([0;1;0],fSail); % Boom control axes
aBoom(:,2) = Cross([0;0;1],fSail);
Aboom   = pinv(aBoom);
mC      = g.body(1).mass.mass;     % Core is body 1
mB      = g.body(2).mass.mass;     % Boom is body 2
rBoomCM = Mag(g.body(2).mass.cM);  % Distance to boom center-of-mass

%-------------------------------

Create the disturbance profile

%-------------------------------

Initial Julian date

%--------------------
p          = ProfileStruct;
p.jD       = JD2000;
p.body     = 2;

% Parameters for the orbit.

We are creating a circular heliocentric orbit.

%-----------------------------------------------
au  = Constant('au'); % Radius in km
mu  = Constant('mu sun');
el  = [au 0 0 0 0.01 0];

Orbit state

%------------
[r0,v0]  = El2RV(el,[],mu);

Initial Quaternion (inertial to body frame)

%--------------------------------------------
[alpha, delta] = LocallyOptimalTraj( 'semi-major axis', r0, v0, mu, -1 );
s     = -Unit(r0);
clock = ClockConversion( alpha, delta, 1, 2, ...
                            struct('r',r0,'v',v0,'s',s,'eciFlag',0) );
clock = pi;
[u,qItoCC] = ConeClockToU( alpha, clock, r0, v0, s );
q0 = qItoCC;

%--------------------------

kN =
     1

Create the data structure

%--------------------------
d          = [];
d.aeroOn   = 0;
d.albedoOn = 0;
d.solarOn  = 1.0;
d.magOn    = 0;
d.radOn    = 0;
d.ggOn     = 1.0;
d.g        = g;
d.mu       = mu;

Orbiting the sun.

%-------------------
d.planet   = 'sun';

Initial state

%--------------
t     = 0;       % time
tO    = dTo;     % Attitude outer loop timer
tG    = dTg;     % Guidance timer
w     = [0;0;0]; % body rates
% Stack states for core and boom
x     = [r0;v0;q0;w;zeros(6,1);QZero;zeros(3,1)];
% Actuator states
boomCM = [0;0];   % Commanded CM for boom

tPlot  = zeros(1,nSim);
xPlot  = zeros(length(x),nSim);
hPlot  = zeros(3,nSim);  % angular momentum
tqPlot = zeros(6,nSim);  % commanded and achieved torque, stacked
aEPlot = zeros(2,nSim);  % Euler angle errors
cMPlot = zeros(2,nSim);  % Commanded center of mass
cCPlot = zeros(2,nSim);  % Commanded cone and clock angles
xOPlot = zeros(6,nSim);
fPlot  = zeros(3,nSim);
cAPlot = zeros(2,nSim);  % Actual cone and clock angles

Simulation loop

%----------------
WaitBarManager( 'initialize', struct('nSamp',nSim,'name','Boom Control Demo') );
tic
for k = 1:nSim
  % Rename variables
  %-----------------
  r     = x(1:3);
  v     = x(4:6);
  rHat  = Unit(r);
  qCore = x(7:10);
  qBoom = x(20:23);

  % Update profile
  %---------------
  p.r  = r;
  p.v  = v;
  p.q  = qCore;
  [angle,u] = Q2AU( qBoom );
  p.angle = angle;
  p.axis  = u;

  %------------------------
  % Guidance
  %------------------------
  if (tG >= dTg)
    % Locally optimal SMA - know that clock angle remains constant.
    [alpha, delta] = LocallyOptimalTraj( 'semi-major axis', r, v, mu, -1 );
    coneC  = alpha;
    clockC = pi;
    tG = 0;
  end

  %---------------------------------------------------------
  % Angle errors
  %---------------------------------------------------------
  [coneA,clockA] = QToConeClock(qCore,r,v,-rHat);
  % Small angle approximation from commanded normal in current body frame
  uSailI = ConeClockToU( coneC, clockC, r, v, -rHat );
  uSailB = QForm( qCore, uSailI );
  errY   = uSailB(3);
  errZ   = -uSailB(2);
  eulErr = [0;errY;errZ];

  %--------------------------------------------------------------
  % Outer attitude loop: Update the boom command at dTo intervals
  %--------------------------------------------------------------
  if (tO >= dTo)

    % Environment - changes slowly
    %-----------------------------
    e = SailEnvironment( 'sun', p, d );

    % Control law and torque
    %-----------------------
    % small angle convention
    angleError = [0;eulErr(2:3)];
    % first compute body acceleration
    accel = cC*xN + dC*angleError;
    % controller state update
    xN    = aC*xN + bC*angleError;
    % convert acceleration to control torque using actual vehicle inertia
    tExt  = -g.mass.inertia*accel;

    % Cp/Cm offset
    %-------------
    % use pinv to allocate torque to controllable axes (Y/Z) via Aboom.
    % assume Cp is at center and compute new Cm from torque and masses.
    % Scale force by cosine of clock angle.
    boomCM = -Aboom/cos(coneA)^2*tExt/(mB/(mC+mB));
    mBoomCM = Mag(boomCM);
    if (mBoomCM >= rBoomCM)
      % requesting CM beyond reach of boom
      hB = 0;
    else
      % Boom unit vector component along normal
      hB = sqrt(rBoomCM^2 - mBoomCM^2);
    end
    % New boom unit vector in core body frame
    uB = Unit([hB;boomCM]);

    % Reset outer timer
    %------------------
    tO = 0;
  end

  % Actuation: Boom equivalent angle and boom body rate (Omega)
  %------------------------------------------------------------
  qBoomError  = U2Q( QTForm(qBoom,[1;0;0]), uB );
  [angleE,uV] = Q2AU( qBoomError );
  aDot        = min( abs(angleE)/dTi, aRateNom );
  Omega       = -sign(angleE)*aDot*uV;

  %--------------------------
  % Compute the disturbances.
  %--------------------------
  [f,tq]  = SailDisturbance( g, p, e, d );
  tqPlot(4:6,k) = tq.total;

  % Store data in plots
  %--------------------
  tPlot(k)    = t;
  xPlot(:,k)  = x;
  aEPlot(1:2,k) = eulErr(2:3);     % store actual Euler errors
  tqPlot(1:3,k) = tExt;
  cMPlot(:,k)   = boomCM;
  fPlot(:,k)    = f.total;
  cAPlot(:,k)   = [coneA;clockA];
  cCPlot(:,k)   = [coneC;clockC];

  %-------------
  % Integrate
  %-------------

  % Distribute momentum
  %--------------------
  % new body rates
  xRates        = x;
  xRates(24:26) = Omega;
  xNew = FMovingBody( 'init', x, xRates, tq, d );

  % Update dynamics
  %----------------
  x    = RK4( @FHingeOrbit, xNew, dTi, t, f, tq, d );

  % Update timers
  %--------------
  t    = t + dTi;
  tO   = tO + dTi;
  tG   = tG + dTi;
  p.jD = p.jD + dTi/86400;


  WaitBarManager( 'update', k ); drawnow;

end
WaitBarManager( 'close' );
toc

Elapsed time is 14.957587 seconds.

Prepare data for plotting

%--------------------------
% scale time vector
[tPlot2, tLabl] = TimeLabl( tPlot );

Create Plots

%-------------
h = [];
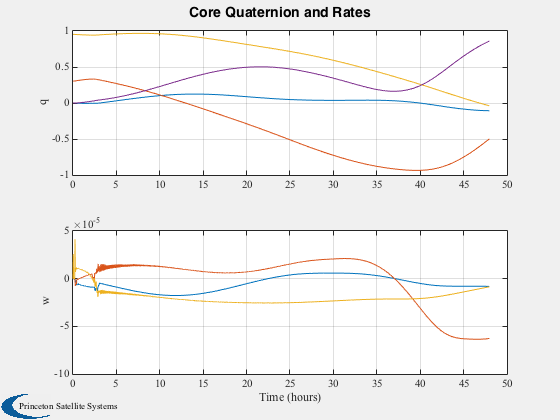
h(1) = Plot2D(tPlot2,xPlot(7:13,:),tLabl,{'q','w'},'Core Quaternion and Rates',...
  'lin',{[1 2 3 4],[5 6 7]});
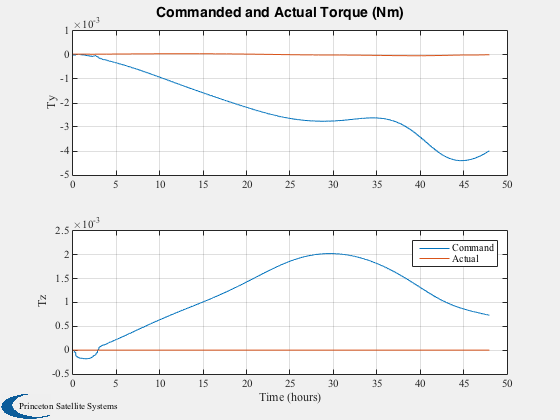
h(2) = Plot2D(tPlot2,tqPlot,tLabl,{'Ty','Tz'},'Commanded and Actual Torque (Nm)',...
           [],{[2 5],[3 6]});
legend('Command','Actual')
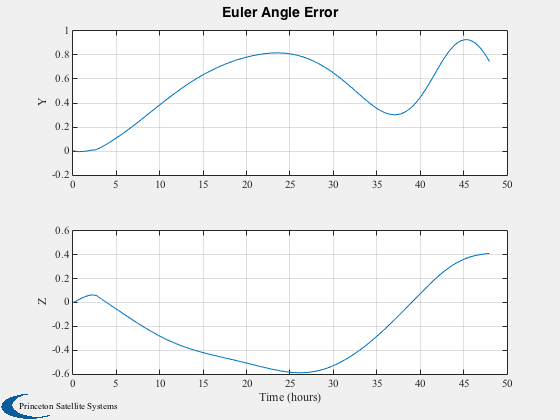
Plot2D(tPlot2,aEPlot,tLabl,{'Y','Z'},'Euler Angle Error');

% Commanded boom CM control
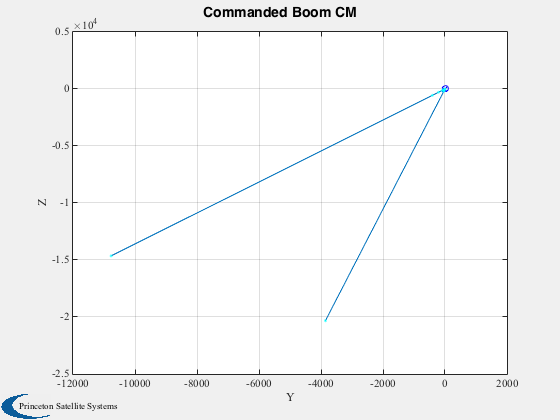
Plot2D(cMPlot(1,:),cMPlot(2,:),'Y','Z','Commanded Boom CM');
hold on
plot(cMPlot(1,1),cMPlot(2,1),'bo');
plot(cMPlot(1,end),cMPlot(2,end),'bx');
plot(cMPlot(1,:),cMPlot(2,:),'c.');

% Resulting guidance trajectory
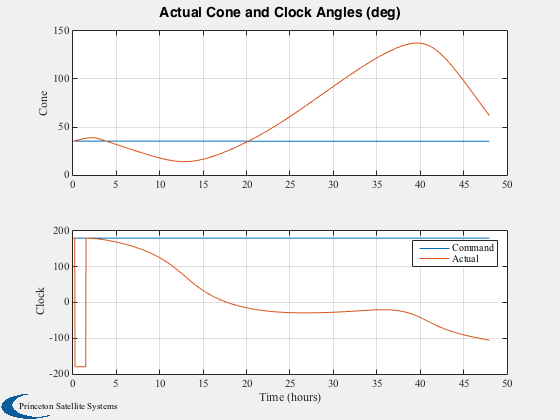
Plot2D(tPlot2,[cCPlot;cAPlot]*180/pi, tLabl, {'Cone','Clock'}, 'Actual Cone and Clock Angles (deg)',...
  'lin',{[1 3],[2 4]})
legend('Command','Actual')

% Orbit
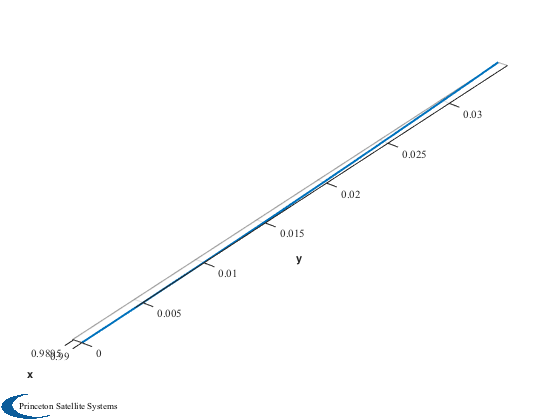
Plot3D(xPlot(1:3,:)/au);
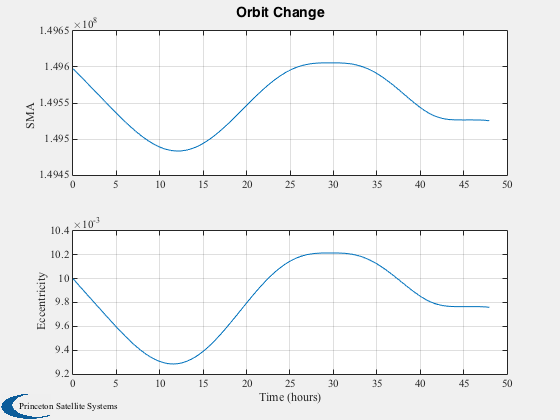
[sma, ecc] = RV2AE( xPlot(1:3,:), xPlot(4:6,:), mu );
Plot2D(tPlot2,[sma;ecc],tLabl,{'SMA','Eccentricity'},'Orbit Change')


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Combined guidance and control demo with fixed rate two-body dynamics.

Contents

Load the control boom sail model

Sim timing

Control parameters - use PIDMIMO to design attitude control loop

Sail physical parameters

Create the disturbance profile

Initial Julian date

We are creating a circular heliocentric orbit.

Orbit state

Initial Quaternion (inertial to body frame)

Create the data structure

Orbiting the sun.

Initial state

Simulation loop

Prepare data for plotting

Create Plots