Simulate inclination change in GEO orbit.

The simulation is run three times, for three different sail areas.
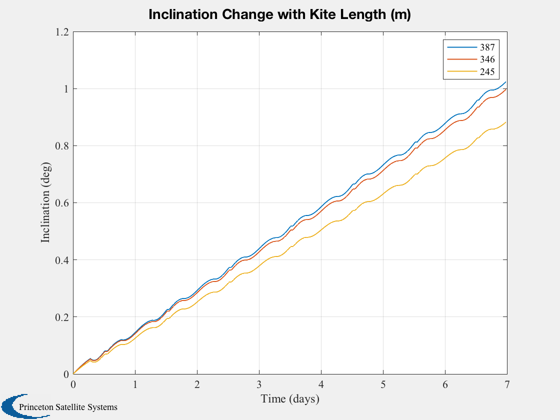
The largest sail modeled can achieve an inclination change of one degree per
week. You can also run the sail perfectly sun-pointing for comparison.

Since version 7.
------------------------------------------------------------------------
See also Cone, NPlot, Plot2D, TimeLabl, Cross, Dot, RK4, Unit, JD2000,
El2RV, RV2El, Eclipse, SunV1, Accel, ConeClockToU, UToConeClock, delta,
EarthGuidance
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%   Copyright (c) 2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

Set up the parameters

%----------------------
mu  = 398600.44; % Earth
Asail = [150000 120000 60000]; % m2
arealDensity = 0.025; % g/m2
mSail = Asail*arealDensity;   % kg
mSC   = [450];
cLight = 3e8;  % m/s
flux   = 1367; % W/m2
m2km   = 0.001;

% ensure one or other is vector, not both
mass  = mSail + mSC;
mSim = length(mass);

% Results
% 2000 m2 sail, 50 kg sail/450 kg bus, 0.1 deg/wk
% 450 kg bus and 25 g/m2,  120000 m2 for 1 deg/wk
% 450 kg bus and 20 g/m2,   60000 m2 for 1 deg/wk
% 450 kg bus and 12.5 g/m2, 28000 m2 for 1 deg/wk

Control method

%---------------
method = 'inc';

Number of sim steps and duration

%---------------------------------
nSim  = 600;
nDays = 7;
dT    = nDays*86400/nSim;

Simulation setup

Plotting array

%---------------
nPlot = zeros(mSim,nSim);
aPlot = zeros(mSim,nSim);
iPlot = aPlot;
ePlot = aPlot;
accPlot = aPlot;
conePlot = aPlot;
clckPlot = aPlot;

Global for the time interface

%------------------------------
global simulationAction
simulationAction = ' ';

d = struct;
d.method = method;

Run the simulation(s)

%----------------------
for j = 1:mSim
  % Assume specular sail
  %---------------------
  acc0 = 2*Asail(j)*flux/cLight/mass(j)*m2km;

  % Initial conditions
  %-------------------
  el0     = [42167 0 0 0 0 0];
  [r0,v0] = El2RV( el0, [], mu );
  x       = [r0;v0];
  jD      = JD2000+90;  % eclipse will be seen for JD2000+90, equinox on 79

  disp('-----------------------------')
  disp(['Simulation ' num2str(j)])
  disp('-----------------------------')
  kS = 1;

  for k = 1:nSim

    % Local variables
    %----------------
    r = x(1:3);
    v = x(4:6);

    % Display the status message
    %---------------------------
    if floor(k/nSim*10) == kS
      disp(['Sim is ' num2str(kS) '0% finished.'])
      kS = kS+1;
    end

    % Control
    %--------
    % First determine sail unit vector.
    [uS, rS] = SunV1( jD );
    d.method = method;
    [q,alphaG,deltaG,u] = EarthGuidance( 0, [r;v], d, struct('uSun',uS) );
    u2 = ConeClockToU( alphaG, deltaG, r, v, uS );

    % Check for eclipses (not common in GEO)
    [n, eclipseType] = Eclipse( r, rS*uS );
    accel          = n*acc0*cos(alphaG);
    aExt           = -accel*u;

    % Plotting
    %---------
    el             = RV2El( r, v, mu )';
    nPlot(j,k)     = n;
    aPlot(j,k)     = el(1);
    iPlot(j,k)     = el(2)*180/pi;
    ePlot(j,k)     = el(5);
    accPlot(j,k)   = accel;
    conePlot(j,k)  = alphaG;
    clckPlot(j,k)  = deltaG;

    % Integrate the trajectory
    %-------------------------
    x  = RK4( 'FOrbCart', x, dT, 0, aExt, mu );
    jD = jD + dT/86400;

  end
end

Plot the results

%-----------------
[t, tL] = TimeLabl( (0:(k-1))*dT );

Plot2D(t,iPlot,tL,'Inclination (deg)', 'Inclination Change with Kite Length (m)')
legend(num2str(sqrt(Asail)',3))
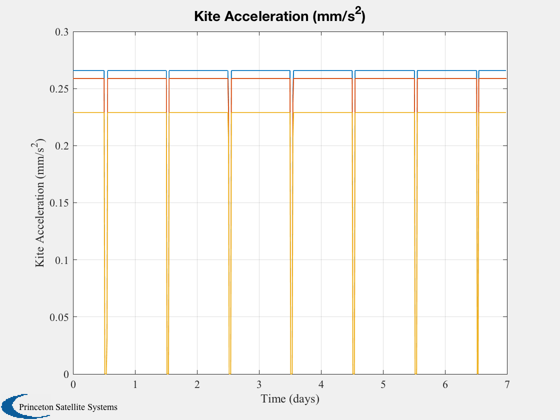
Plot2D(t,accPlot*1e6,tL,'Kite Acceleration (mm/s^2)')
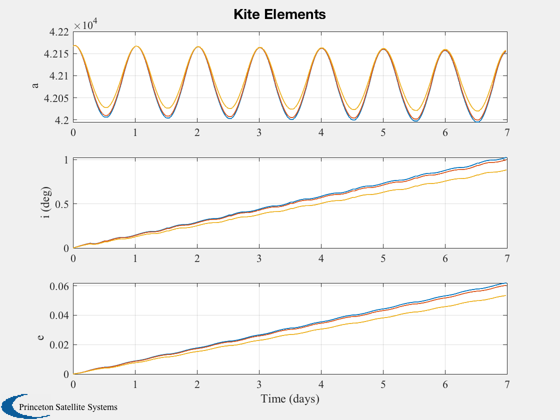
Plot2D(t,[aPlot;iPlot;ePlot],tL,{'a' 'i (deg)' 'e'},['Kite Elements'],'lin',...
  {[1 2 3],[4 5 6],[7 8 9]})
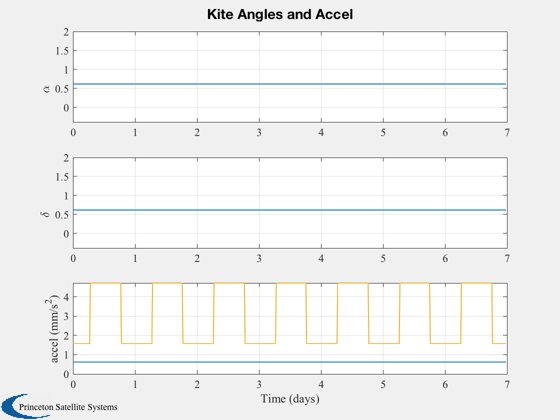
Plot2D(t,[conePlot;clckPlot;accPlot*1e6],tL,{'\alpha' '\delta' 'accel (mm/s^2)'},...
  ['Kite Angles and Accel'],'lin',{1,2,[3 4 5]})

%--------------------------------------
% PSS internal file version information
%--------------------------------------

-----------------------------
Simulation 1
-----------------------------
Sim is 10% finished.
Sim is 20% finished.
Sim is 30% finished.
Sim is 40% finished.
Sim is 50% finished.
Sim is 60% finished.
Sim is 70% finished.
Sim is 80% finished.
Sim is 90% finished.
Sim is 100% finished.
-----------------------------
Simulation 2
-----------------------------
Sim is 10% finished.
Sim is 20% finished.
Sim is 30% finished.
Sim is 40% finished.
Sim is 50% finished.
Sim is 60% finished.
Sim is 70% finished.
Sim is 80% finished.
Sim is 90% finished.
Sim is 100% finished.
-----------------------------
Simulation 3
-----------------------------
Sim is 10% finished.
Sim is 20% finished.
Sim is 30% finished.
Sim is 40% finished.
Sim is 50% finished.
Sim is 60% finished.
Sim is 70% finished.
Sim is 80% finished.
Sim is 90% finished.
Sim is 100% finished.

Published with MATLAB® R2019a