Simulate a solar sail in orbit near the earth and moon.

Uses two stored gravity files:
*EarthGravityModel.mat
*LunarGravityModel.mat.

Currently two options for ephemeris. True inertial ephemeris uses MoonV1 for the moon location and SunV1 for the sun. The simplified version assumes a circular moon orbit and neglects the inclination of the sun line with respect to the Earth-Moon system plane.

Since version 7.
------------------------------------------------------------------------
See also FSailEarthMoon, FEarthMoonSun, LunarHalo. , InformDlg, Plot2D,
Plot3D, PlotPlanet, TimeLabl, TitleS, Cross, Mag, Unit, Date2JD,
EarthMoonRotFrame, El2RV, RVFromKepler, MoonEl, MoonV1
------------------------------------------------------------------------

Main simulation parameters
Gravity model parameters
Epoch and orbit
Create initial conditions in inertial frame
The number of steps
Create the time array
Specify the ode113 accuracy
Integrate
Plot the orbit
Plot the earth, moon and trajectory in 3D
Plot

%--------------------------------------------------------------------------
%  Copyright (c) 2004, 2007 Princeton Satellite Systems, Inc.
%  All rights reserved.
%--------------------------------------------------------------------------

Main simulation parameters

%---------------------------
d = struct('mass',500);
% 0.3 mm/s at L1 (inside moon)
% 0.2 mm/s at L2 (outside moon)
d.accel = 3e-7;
% Select Lagrange point (1 is inside moon orbit, 2 is outside)
kLP     = 1;
% Ephemeris selection
inertial = false;

Gravity model parameters

%-----------------------------------
d.earth = load('EarthGravityModel.mat');
d.moon  = load('LunarGravityModel.mat');
% Specify zero harmonics for point-mass models
d.earth.nZ = 0;
d.earth.nT = 0;
d.moon.nZ  = 0;
d.moon.nT  = 0;

Epoch and orbit

%----------------
d.jDStart       = Date2JD; % Today
d.muSun         = 1.327124e+11;
theta           = 0;
[r0,xL,wS,O,rM] = LunarHalo( d.accel, kLP, theta, d.moon.mu, d.earth.mu );
vy              = r0(2)*wS;
mu              = d.moon.mu/(d.moon.mu + d.earth.mu);

if inertial
  % True inertial coordinates using MoonV1
  d.el            = [];
  [u1, rho1]      = MoonV1( d.jDStart );
  dT              = 28/4;
  [u2, rho2]      = MoonV1( d.jDStart + dT );
  rMoon           = u1*rho1;
  hMoon           = Unit(Cross(u1,u2));
  yMoon           = Cross(hMoon,u1);
  mRotToECI       = [u1 yMoon hMoon];
else
  % Simple circular coordinates using MoonEl
  d.el = MoonEl( d.jDStart );
  d.el(5) = 0;
  d.el(1) = rM;
  [rMoon,vMoon] = El2RV( d.el );
  hMoon = Unit(Cross(rMoon,vMoon));
  u1    = Unit(rMoon);
  yMoon = Cross(hMoon,u1);
  mRotToECI = [u1 yMoon hMoon];
end

Create initial conditions in inertial frame

%--------------------------------------------
rSail = (xL + mu)*rMoon + mRotToECI*[r0(1);0;r0(3)];
% v inertial = v rotating + w x r
vSail = vy*yMoon + Cross(O*hMoon,rSail);
x0    = [rSail;vSail];

The number of steps

%--------------------
nSim = 800;

Create the time array

%----------------------
nDays         = 7;
tDuration     = nDays*86400;
t             = linspace(0,tDuration,nSim);

Specify the ode113 accuracy

%----------------------------
xODEOptions   = odeset( 'AbsTol', 1e-16, 'RelTol', 1e-13 );

d.force = 0;

Integrate

%----------
hDlg = InformDlg( 'Integrating...', 'LunarHaloDemo' );
[tOut, yOut] = ode113( 'FSailEarthMoon', t, x0, xODEOptions, d );
close(hDlg);

xPlot = yOut';
[tPlot,tLabl] = TimeLabl( tOut' );

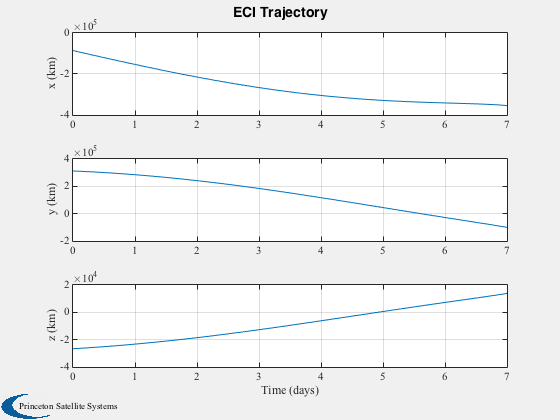
Plot the orbit

%---------------
Plot2D( tPlot, xPlot(1:3,:), tLabl, {'x (km)' 'y (km)' 'z (km)'}, 'ECI Trajectory' );

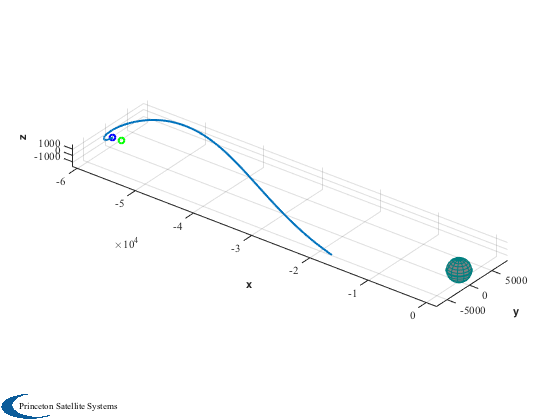
Plot the earth, moon and trajectory in 3D

%------------------------------------------
jDPlot = d.jDStart + tOut'/86400;

if inertial
  % Full inertia sim also using MoonV1
  EarthMoon( xPlot(1:3,:), jDPlot, [3 10] );
  TitleS(sprintf('Inertial Trajectory Near L%i',kLP))

  EarthMoonRotFrame( xPlot(1:3,:), jDPlot, [3 5] )

  [uMP, rMP] = MoonV1( jDPlot );

else
  % Simplified sim
  [rM,vM] = RVFromKepler( d.el, tOut' );
  uMP = Unit( rM );
  rMP = Mag( rM );

end

% Devolve back into relative frame
yMoon = Cross(hMoon,uMP);
xRot  = zeros(3,nSim);
for k = 1:nSim
  mRotToECI = [uMP(:,k) yMoon(:,k) hMoon];
  xRot(:,k) = mRotToECI'*(xPlot(1:3,k) - uMP(:,k)*rMP(k));
end

Plot

xLPlot = [(xL+mu-1)*rMP;zeros(2,nSim)];
Plot3D( xRot(1:3,:) )
PlotPlanet([0;0;0],d.moon.a);
hold on
plot3(xLPlot(1,:),xLPlot(2,:),xLPlot(3,:),'g','linewidth',2)
plot3(xLPlot(1,1),xLPlot(2,1),xLPlot(3,1),'go','linewidth',2)
plot3(xRot(1,1),xRot(2,1),xRot(3,1),'bo','linewidth',2)


%--------------------------------------
% PSS internal file version information
%--------------------------------------