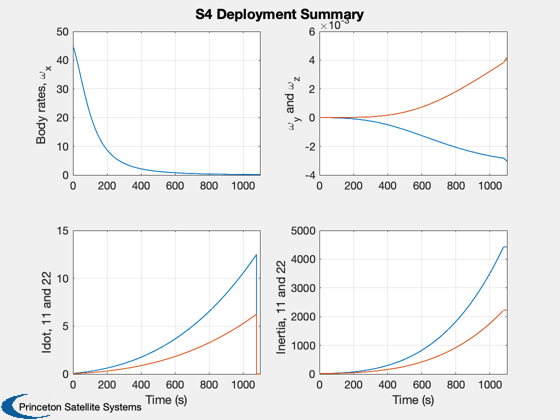
S4 (ATK's scalable sail) deployment demo.

Notes:
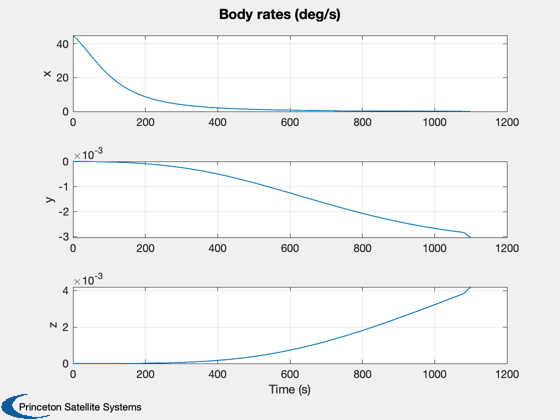
   Unable to replicate steepness of curve in roll rate plots.
   Otherwise behavior of plots similar for full RHS and simplified version
   from paper.

Functions demonstrated:
   S4Deploy, CAD model
   IDotS4, inertia derivative function
   FTimeVaryingI, attitude dynamics
   S4DeployTorque, disturbance model

Since version 7.
------------------------------------------------------------------------
Reference: LeFevre and Jha, (Student Paper) Attitude Dynamics and Stability
of Solar Sails During Deployment.  AIAA-2006-1704
------------------------------------------------------------------------
See also DrawSCPlanPlugIn, Q2Eul, QZero, InformDlg, Plot2D, Rename,
FTimeVaryingI, FS4Deployment, FSailCombined, IDotS4, S4DeployTorque
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%	Copyright (c) 2006 Princeton Satellite Systems, Inc.
%   All rights reserved.
%-------------------------------------------------------------------------------

clear force; clear torque; clear d;

%%%%%%%%%%%%%%%%%%
% User options
% Choose model from student paper or full model (same results)
model = 'full';  % 'student' or 'full'
%%%%%%%%%%%%%%%%%%

d = FSailCombined;

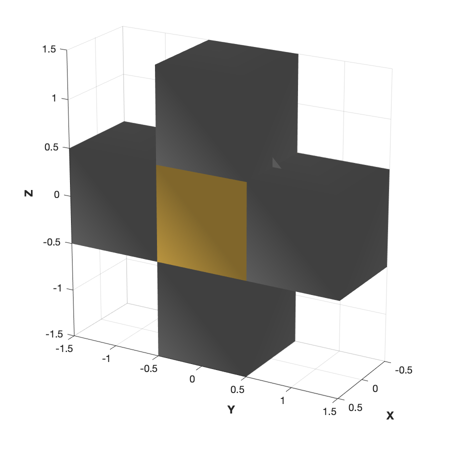
Load and draw the model

%------------------------
d.g = load('S4PreDeploy.mat');
g2  = load('S4Deployed.mat');
DrawSCPlanPlugIn( 'initialize', d.g );
view(120,20)
drawnow
Rename('Pre-Deployment Model')
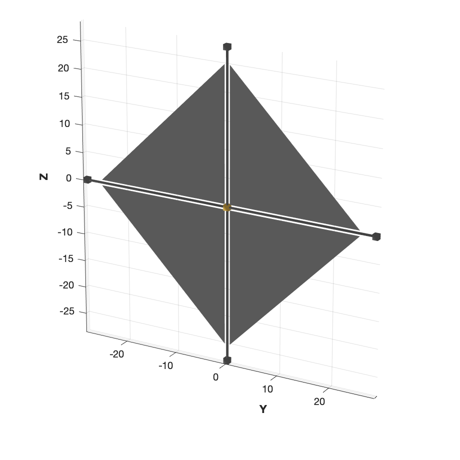
DrawSCPlanPlugIn( 'initialize', g2 );
view(120,20)
drawnow
Rename('Deployed Model')

Deployment data

%----------------
d.Ldot = 0.025;        % m/s, rate of mast extension
d.fInertia = @IDotS4;  % inertia derivative function

Apply a fixed torque for cp/cm offset

%--------------------------------------
eps = 0.1;    % m (0.25% uncertainty on 40 m sail)
d.F = 0.01;   % N
Tz  = eps*d.F;

Set tolerances

%---------------
xODEOptions = odeset( 'AbsTol', 1e-8, 'RelTol', 1e-5 );

Assemble the state vector. Inertia is last.

%--------------------------------------------
x0  = [zeros(6,1);QZero;[45*pi/180;0;0];reshape(d.g.mass.inertia,9,1)];

Propagator

%-----------
force.total = [d.F;0;0];
torque.total = [0;0;Tz];

hDlg = InformDlg( 'Integrating...', 'S4Deployment' );
switch model
  case 'full'
    % assume a constant torque
    d.ephemeris   = 'NoEphemeris';
    d.disturbance = @S4DeployTorque;
    d.attitude    = @FTimeVaryingI;
    d.environment = 'NoEnvironment';
    d.orbit       = 'NoOrbit';
    [z, x] = ode113( @FSailCombined, [0 1100], x0, xODEOptions, [], d );
  case 'student'
    % scales the torque with deployment (embedded)
    [z, x] = ode113( @FS4Deployment, [0 1100], x0, xODEOptions, force, torque, d );
end
close(hDlg);

x      = x';
t      = z';
nSim   = length(t);

Obtain Idot post-integration

%-----------------------------
Idot = IDotS4( t, d );

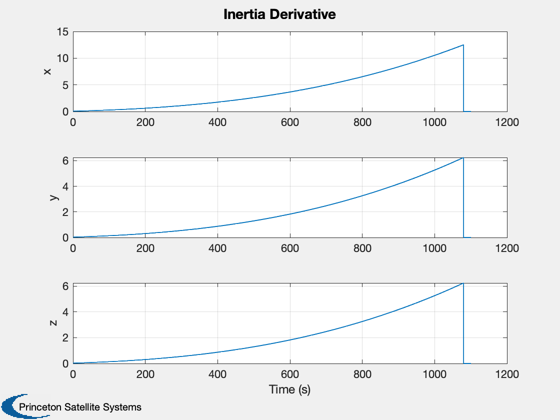
Plot inertia

%-------------
Plot2D(t,Idot,'Time (s)',{'x','y','z'},'Inertia Derivative')
I = x([14 18 22],:);
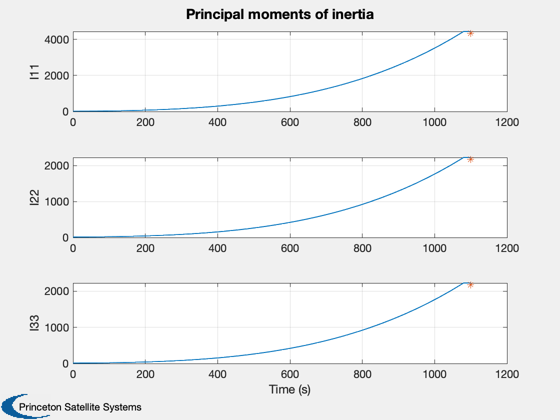
Plot2D(t,I,'Time (s)',{'I11','I22','I33'},'Principal moments of inertia')
subplot(3,1,1)
hold on; plot(t(end),g2.mass.inertia(1,1),'*');
subplot(3,1,2)
hold on; plot(t(end),g2.mass.inertia(2,2),'*');
subplot(3,1,3)
hold on; plot(t(end),g2.mass.inertia(3,3),'*');

Plot rates and angles

%----------------------
w = x(11:13,:)*180/pi;
Plot2D(t,w,'Time (s)',{'x','y','z'},'Body rates (deg/s)')
eul = zeros(3,nSim);
for k = 1:nSim
  eul(:,k) = Q2Eul(x(7:10,k));
end
eul(1,:) = unwrap(eul(1,:));
eul = eul*180/pi;
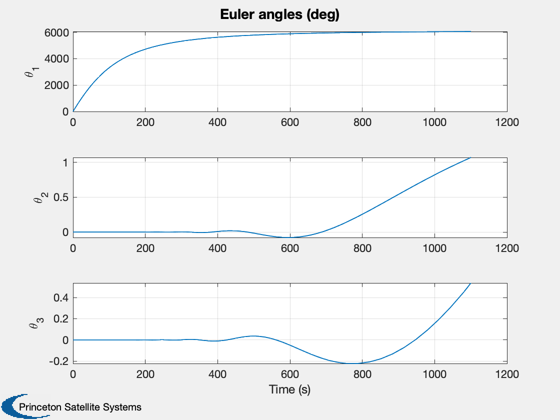
Plot2D(t,eul,'Time (s)',{'\theta_1','\theta_2','\theta_3'},'Euler angles (deg)')

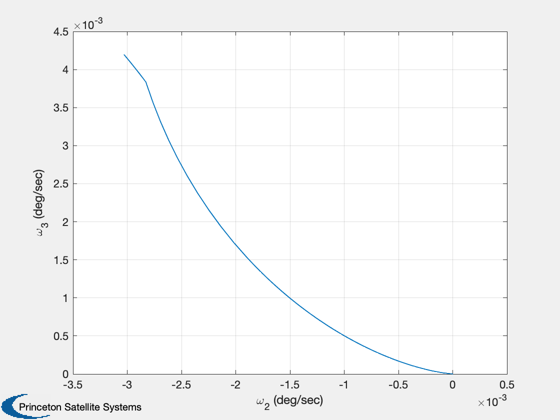
Plot2D(w(2,:),w(3,:),'\omega_2 (deg/sec)','\omega_3 (deg/sec)',' ')
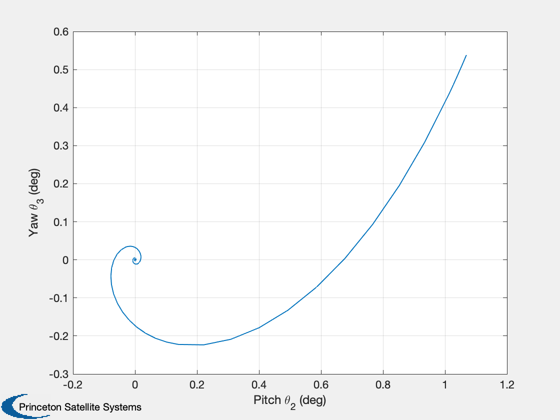
Plot2D(eul(2,:),eul(3,:),'Pitch \theta_2 (deg)','Yaw \theta_3 (deg)',' ')

% summary plot page
Plot2D(t,[w;Idot(1:2,:);I(1:2,:)],'Time (s)',{'Body rates, \omega_x','\omega_y and \omega_z',...
  'Idot, 11 and 22','Inertia, 11 and 22'},...
  'S4 Deployment Summary',[],{1, [2 3],[4 5],[6 7]},[],2)


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2020a