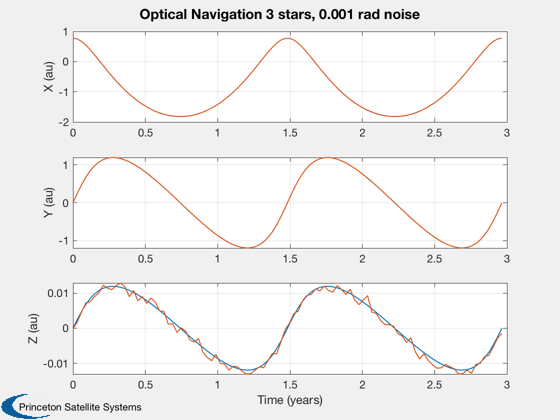
Estimate the orbit position using a range and three stars

Assume the spacecraft is orbiting the Sun and measure n star vectors. We assume we know range, but the diameter of the sun could also be used.

If you add noise you will notice that the z-position is the noisiest.

This is the basis for optical navigation.

%--------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2020 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2020.1
%--------------------------------------------------------------------------

% Select the number of stars to use
nStars    = 3;
% Select the amount of noise to add (radians)
% Noise is added to the measured angle between the stars and the sun.
oneSigma  = 1e-3;

% Create an orbit
mu      = Constant('mu sun');
aU      = Constant('au');
el      = [1.3*aU 0.01 0 0 0.4 0];
p       = Period(el(1),mu);
t       = linspace(0,2*p);
r       = RVOrbGen(el,t,[],mu)/aU;
n       = length(t);

Plot3D(r,'X (au)','Y (au)','Z (au)','Heliocentric Orbit');
hold on
plot3(0,0,0,'.','markersize',30,'color',[1 0.8314 0.4745]);
rotate3d on

% Get the range
range     = Mag(r);
uR        = Unit(r);

% Use any set of stars
u         = Unit(rand(3,nStars));
uT        = u';
pUT       = pinv(uT);

% One position
rMeas = zeros(3,n);
for k = 1:n
  ang         = acos(uT*uR(:,k)) + oneSigma*rand(nStars,1);
  rMeas(:,k)  = range(k)*pUT*cos(ang);
end

[t,tL] = TimeLabl(t);

s = sprintf('Optical Navigation %d stars, %5.3f rad noise',nStars,oneSigma);

Plot2D(t,[r;rMeas],tL,{'X (au)','Y (au)','Z (au)'},s,...
  'lin', {'[1 4]' '[2 5]' '[3 6]'});


%--------------------------------------