Demonstrate orbit estimation using a UKF and optical navigation.

This tests orbit determination using two planets and a star.

------------------------------------------------------------------------- See also UnitVectorFromOffset, Plot2D, TimeLabl, RK4, Unit, Date2JD, OpticalNavigationMeasurement, UKF, Planets -------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright 2006, 2009 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 8.
%--------------------------------------------------------------------------

Select the filter

%------------------
filter        = @UKF;   % Full covariance matrix filter

Measurement options

%--------------------
planets       = 1; % 1 or 2
starOffset    = 8*pi/180;

Simulation parameters

%----------------------
nSim          = 8000;
dT            = 2000; % sec
tEnd          = nSim*dT;

Astronomical unit

%------------------
au            = 149597870; % km/au

Allocate memory for plotting

%-----------------------------
if( planets == 2 )
	xP  = zeros(17,nSim);
else
	xP  = zeros(14,nSim);
end

Sun gravitational parameter

%----------------------------
mu            = 132712438000;

Initial Julian Date

%--------------------
jD0           = Date2JD( [2006 2 1 0 0 0] );

Parameters for Earth and Mars

%------------------------------
thetaE        = 2.30768364684019; % Initial orbit angle of the Earth (rad)
thetaM        = 1.56042659846335; % Initial orbit angle of Mars (rad)
omegaE        = sqrt(mu/au^3); % Earth orbit rate
omegaM        = sqrt(mu/(1.52*au)^3); % Mars orbit rate
t             = linspace(0,tEnd,nSim);
a             = omegaE*t + thetaE;
rE            = au*[cos(a);sin(a);zeros(1,nSim)]; % Earth orbit
a             = omegaM*t + thetaM;
rM            = 1.52*au*[cos(a);sin(a);zeros(1,nSim)]; % Mars orbit

Initial state [r;v]

%---------------------
x             = [rE(:,1) - [3e6;1e6;0];-33;-24;-10];

Position and velocity uncertainty

%----------------------------------
r1Sigma       = 100; % km
v1Sigma       = 0.1; % km/s

% Measurement noise
% Errors: Earth radius 0.01 km, Mars radius 0.1 km, ephem 2 km
% The elements are the noise for the following measurements
%   chord of planet 1
%   angle between star and planet 1
%   chord of planet 2
%   angle between star and planet 2

angle between planet 1 and planet 2

%-------------------------------------------------------------
sigY          = 1e-1*[1e-6;1e-5;1e-6;1e-5;1e-5];

State estimate at start

%------------------------
d.x           = x + [r1Sigma*randn(3,1);v1Sigma*randn(3,1)];

Covariance based on the uncertainty

%------------------------------------
d.p           = diag([r1Sigma^2*ones(1,3) v1Sigma^2*ones(1,3)]);
d.int         ='RK4';
d.rHSFun      ='RHSOrbitUKF';
d.measFun     ='OpticalNavigationMeasurement';
d.integrator  = @RK4;
d.alpha       = 0.8e-3; % UKF spread of sigma points
d.kappa       = 0; % UKF weighting factor
d.beta        = 2; % UKF incorporation of a priori knowledge
d.dY          = (planets - 1)*3 + 2;
d.dT          = dT;
d.rHSFunData  = struct('mu',mu,'a',[0;0;0]);
d.rM          = diag(sigY(1:d.dY).^2); % Measurement noise covariance
vecP          = [0 0 0 1e-6 1e-6 1e-6]';
d.rP          = diag(vecP.^2); % Plant noise covariance
d             = filter('initialize', d );
t             = 0;

Measurement parameters that don't change

%-----------------------------------------
clear g
g.a1          = 6378;
u1            = Unit([0 .1 -0.2;0 -0.3 0.1;1 1 1]);
g.u1          = u1(:,1);
g.l1          = rE(:,1);
j             = 1;

if( planets == 2 )
	g.a2 = 3397;
	g.u2 = [0;0;1];
	g.l2 = rM(:,1);
end

y = OpticalNavigationMeasurement( x(1:3), g );

for k = 1:nSim

  % Plotting
  %---------
  xP(:,k) = [d.x; x; y];

  % Update the RHS
  %---------------
  x       = RK4( d.rHSFun, x, dT, t, d.rHSFunData ) + vecP.*randn(6,1);
  t       = t + dT;

  % Measurements
  %-------------
  g.l1          = rE(:,k);

  if( planets == 2 ) % Adding 2nd planet measurement
    g.l2 = rM(:,k);
    g.u1 = UnitVectorFromOffset( rE(:,k), x(1:3), starOffset );
    g.u2 = UnitVectorFromOffset( rM(:,k), x(1:3), starOffset );
  else
    g.u1 = u1(:,j);
    j    = j + 1;
    if( j > 3 )
        j = 1;
    end
  end

  d.measFunData = g;
  if( planets == 2 )
    y  = OpticalNavigationMeasurement( x(1:3), g ) + sigY.*randn(5,1);
  else
    y  = OpticalNavigationMeasurement( x(1:3), g ) + sigY(1:2).*randn(2,1);
  end

  % Kalman Filter
  %--------------
  d.t           = t;
  d             = filter( 'update', d, y );
end

Create a time sequence for the x-axis

%--------------------------------------
[t,tL,tU] = TimeLabl((0:(nSim-1))*dT);

Plot

%-----
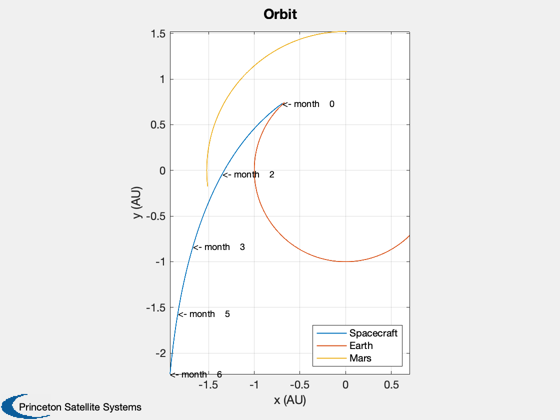
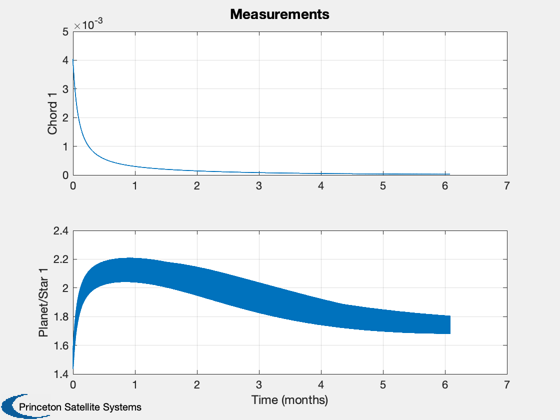
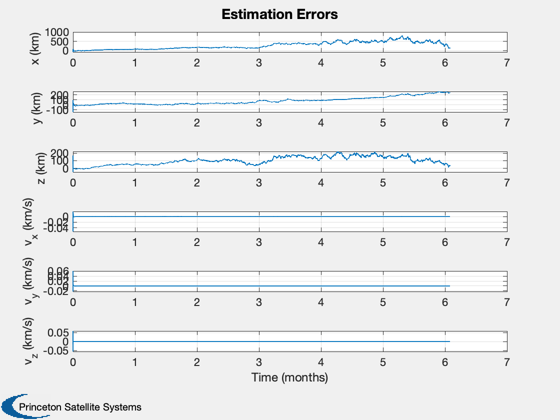
yL = {'x (km)' 'y (km)' 'z (km)' 'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)' };
Plot2D( [xP(7,:); rE(1,:); rM(1,:)]/au, [xP(8,:); rE(2,:); rM(2,:)]/au, 'x (AU)', 'y (AU)', 'Orbit' );
axis image
i = floor(linspace(1,nSim,5));
for k = 1:5
    text( xP(7,i(k))/au, xP(8,i(k))/au,sprintf('<- %s %4.0f',tU,t(i(k))),'fontsize',9);
end

legend({'Spacecraft' 'Earth' 'Mars'}, 'location', 'southeast')

if( planets == 2 )
    yL = {'Chord 1', 'Planet/Star 1', 'Chord 2', 'Planet Star 2',' Planet/Planet'};
    Plot2D( t, xP(13:17,:), tL, yL, 'Measurements' );
else
    yL = {'Chord 1', 'Planet/Star 1'};
    Plot2D( t, xP(13:14,:), tL, yL, 'Measurements' );
end

err = xP(1:6,:) - xP(7:12,:);
yL  = {'x (km)' 'y (km)' 'z (km)' 'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)'};
Plot2D( t, err, tL, yL, 'Estimation Errors' );

%--------------------------------------

Published with MATLAB® R2020a