Demonstrate orbit estimation using a UKF and planet centroid data.

The spacecraft can be in the Messenger or New Horizons orbits. Uses the Hipparcos catalog.

Since version 9.
-------------------------------------------------------------------------
See also RaDec2U, Constant, Plot2D, TimeLabl, RK4,
NavTargetTrackingPlanetary, OpticalNavPlanetStar,
OpticalNavPlanetStarNoiseMatrix, LoadCatalog, UKF, Planets
-------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright 2009-2010 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------


clear g; clear d; clear noise;

Constants

%----------
au          = Constant('au');

years       = 6;

planet      = Planets('rad',1:9);

pixel       = 10e-3; % mm
fL          = 200; % mm
centroiding = 0.1; % pixel

Select a mission

%------------------
mission     = 'messenger';
mission     = 'new horizons';

switch mission
    case 'messenger'
        x = [-5.102050761318097E+07; -3.914630171469574E+07; -1.563888544075625E+07;...
              2.159852087150890E+01; -3.063444535492430E+01; -1.827429443660471E+01];

        jD0 = 2455755.50;
    case 'new horizons'

        x   = [-6.983445814653811E+07; -1.441036100591167E+09; -5.821377265514169E+08;...
                5.922525925977417E+00; -1.594089850539337E+01; -6.215007577164026E+00];
        jD0 = 2454660.5;
end

Select the filter

%------------------
filter        = @UKF;   % Full covariance matrix filter

Measurement options

%--------------------
g.fOV         = 8.8*pi/180;

Simulation parameters

%----------------------
nSim          = years*24*365;
dT            = 3600; % sec
tEnd          = nSim*dT;

Allocate memory for plotting

%-----------------------------
xP            = zeros(13,nSim);

Earth gravitational parameter

%----------------------------
mu            = Constant('mu sun');

Star Catalog

%-------------
starCatalog   = LoadCatalog( 'Hipparcos', 7 );
g.uSCatalog   = RaDec2U( starCatalog.rA, starCatalog.dec );
g.pCatalog    = Planets('rad',1:9);

Position and velocity uncertainty

%----------------------------------
r1Sigma       = 1; % km
v1Sigma       = 0.0001; % km/s

Measurement noise

%------------------
noise.angle       = 10*0.0000048481368111; % 1 arcsecond in radians
noise.planet      = [1 1 1 1 100 600 1250 2250 2800];
noise.radius      = [1 1 0.01 .1 6 6 7 19 6 140];
noise.pixelAngle  = atan(centroiding*pixel/fL);

State estimate at start

%------------------------
d.x                      = x + [r1Sigma*randn(3,1);v1Sigma*randn(3,1)];
d.x                      = x;

Covariance based on the uncertainty

%------------------------------------
d.p                      = diag([r1Sigma^2*ones(1,3) v1Sigma^2*ones(1,3)]);
d.int                    ='RK4';
d.rHSFun                 ='RHSOrbitUKF';
d.measFun                ='OpticalNavPlanetStar';
d.integrator             = @RK4;
d.alpha                  = 0.8e-3; % UKF spread of sigma points
d.kappa                  = 0; % UKF weighting factor
d.beta                   = 2; % UKF incorporation of a priori knowledge
d.dT                     = dT;
d.rHSFunData             = struct('mu',mu,'a',[0;0;0]);
vecP                     = [0 0 0 1e-6 1e-6 1e-6]';
d.rP                     = diag(vecP.^2); % Plant noise covariance
d                        = filter('initialize', d );
t                        = 0;
g.planet                 = planet;
g.trackPlanet            = 1;
g.trackCount             = 0;
g.trackCountMax          = 10;
g.kP                     = 0;

Initialize the time display

%----------------------------
TimeDisplay( 'initialize', 'Optical Navigation Sim', nSim )


for k = 1:nSim


  % Display the status message
  %---------------------------
  TimeDisplay( 'update' );


  % Plotting
  %---------
  xP(:,k)                   = [d.x; x; g.kP];

  % Update the RHS
  %---------------
  x                         = RK4( d.rHSFun, x, dT, t, d.rHSFunData );
  t                         = t + dT;

  % Measurements
  %-------------
  g.jD                      = jD0 + t/86400;
  g.mode                    = 'polar star';
  g                         = NavTargetTrackingPlanetary( x, g );
  y                         = OpticalNavPlanetStar( x, g, noise );

  % Kalman Filter
  %--------------
  d.measFunData             = g;
  [d.dY, d.rM]              = OpticalNavPlanetStarNoiseMatrix( g, x(1:3), noise );
  d.t                       = t;
  d                         = filter( 'update', d, y );

end

TimeDisplay( 'close' );

Create a time sequence for the x-axis

%--------------------------------------
[t,tL] = TimeLabl((0:(nSim-1))*dT);

Plot

%-----
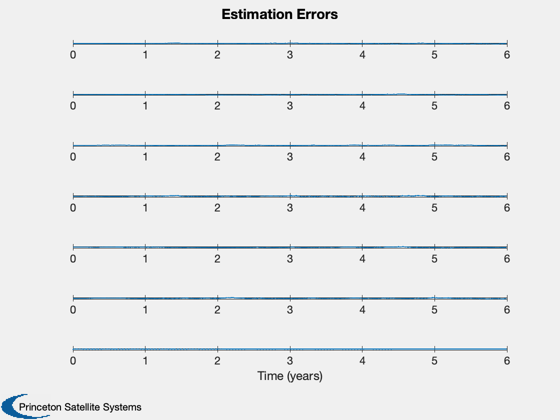
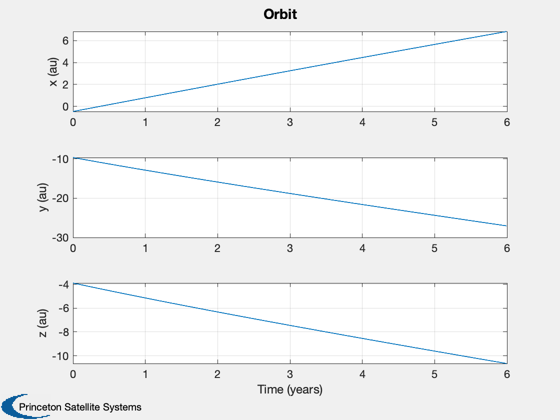
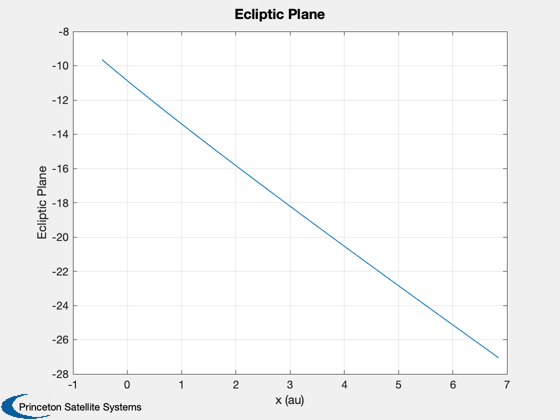
err = xP(1:6,:) - xP(7:12,:);
yL  = {'x (km)' 'y (km)' 'z (km)' 'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)', 'Planet id'};
Plot2D( t, [err;xP(13,:)], tL, yL, 'Estimation Errors' );
Plot2D( t, xP(7:9,:)/au, tL, {'x (au)' 'y (au)' 'z (au)'}, 'Orbit' );
Plot2D( xP(7,:)/au, xP(8,:)/au, {'x (au)', 'y (au)'}, 'Ecliptic Plane')

rng = floor(0.75*nSim):nSim;
err = err(:,rng);
meanSquareError = mean(sqrt(err.^2),2)


%--------------------------------------
% PSS internal file version information
%--------------------------------------

meanSquareError =
       2284.2
       2319.6
       2688.1
   8.6891e-05
   0.00019067
   0.00019401

Published with MATLAB® R2020a