Demonstrate orbit estimation using a UKF and lunar landmark data.

The spacecraft is in a geosynchronous orbit. Uses the Hipparcos catalog.

------------------------------------------------------------------------- See also RaDec2U, Plot2D, TimeLabl, RK4, Unit, Date2JD, NavTargetTrackingLunar, OpticalNavLunarLandmarkStar, LoadCatalog, UKF, Planets, AngleOfView -------------------------------------------------------------------------

Select the filter
Measurement options
Simulation parameters
Allocate memory for plotting
Earth gravitational parameter
Initial Julian Date
Star Catalog
Initial state [r;v]
Position and velocity uncertainty
Measurement noise
Landmark vectors
State estimate at start
Covariance based on the uncertainty
Create a time sequence for the x-axis
Plot

%--------------------------------------------------------------------------
%   Copyright 2009-2010, 2014 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since version 9.
%--------------------------------------------------------------------------

Select the filter

%------------------
filter        = @UKF;   % Full covariance matrix filter

Measurement options

%--------------------
planets       = 1; % 1 or 2
starOffset    = 8*pi/180;
radiusMoon    = 1738;
fOV           = 8.8*pi/180;
fL            = 200;
pixel         = 15e-3; % mm
nPixels       = 2048;
rMoon         = 405696 + 42167; % Maximum apogee
angle         = AngleOfView( fL, nPixels*pixel ); % half angle
angleMoon     = atan(radiusMoon/rMoon); % half angle
pixelsMoon    = 0.5*nPixels*angleMoon/angle;
resolution    = radiusMoon/pixelsMoon;

Simulation parameters

%----------------------
nSim          = 24*20;
dT            = 3600; % sec
tEnd          = nSim*dT;

Allocate memory for plotting

%-----------------------------
xP            = zeros(12,nSim);

Earth gravitational parameter

%----------------------------
mu            = 3.98600436e5;

Initial Julian Date

%--------------------
jD0           = Date2JD( [2014 2 1 0 0 0] );

Star Catalog

%-------------
starCatalog   = LoadCatalog( 'Hipparcos', 7 );
uStar         = RaDec2U( starCatalog.rA, starCatalog.dec );

Initial state [r;v]

%---------------------
r             = 42167;
x             = [r;0;0;0;sqrt(mu/r);0];

Position and velocity uncertainty

%----------------------------------
r1Sigma       = 100; % km
v1Sigma       = 0.1; % km/s

Measurement noise

%------------------
noise.landmark = resolution/sqrt(12);% 30e-3; % 30 m
noise.angle    = 10*0.0000048481368111; % 1 arcsecond in radians
noise.moon     = 3e-5; % 3 cm

Landmark vectors

%-----------------
rL   = radiusMoon*Unit([1   0.5 0.3 0.5 0.8 0.2;...
                        0   0.5 0.3 0.8 0.2 0.1;...
                        0.5 0.5 0.5 0.5 0.5 0.5]);

State estimate at start

%------------------------
d.x           = x + [r1Sigma*randn(3,1);v1Sigma*randn(3,1)];

Covariance based on the uncertainty

%------------------------------------
d.p           = diag([r1Sigma^2*ones(1,3) v1Sigma^2*ones(1,3)]);
d.int         ='RK4';
d.rHSFun      ='RHSOrbitUKF';
d.measFun     ='OpticalNavLunarLandmarkStar';
d.integrator  = @RK4;
d.alpha       = 0.8e-3; % UKF spread of sigma points
d.kappa       = 0; % UKF weighting factor
d.beta        = 2; % UKF incorporation of a priori knowledge
d.dY          = 12;
d.dT          = dT;
d.rHSFunData  = struct('mu',mu,'a',[0;0;0]);
sigY          = noise.angle*10*ones(1,12);
d.rM          = diag(sigY.^2); % Measurement noise covariance
vecP          = [0 0 0 1e-6 1e-6 1e-6]';
d.rP          = diag(vecP.^2); % Plant noise covariance
d             = filter('initialize', d );
t             = 0;
[g.u, g.rL]   = NavTargetTrackingLunar( x, uStar, rL, jD0, fOV );
g.jD          = jD0;
y             = OpticalNavLunarLandmarkStar( x, g );

for k = 1:nSim

  % Plotting
  %---------
  xP(:,k)       = [d.x; x];

  % Update the RHS
  %---------------
  x             = RK4( d.rHSFun, x, dT, t, d.rHSFunData ) + vecP.*randn(6,1);
  t             = t + dT;
  jD            = jD0 + t/86400;
  g.jD          = jD;
  [g.u, g.rL]   = NavTargetTrackingLunar( x, uStar, rL, jD, fOV );
  y             = OpticalNavLunarLandmarkStar( x, g, noise );
  d.measFunData = g;

  % Kalman Filter
  %--------------
  d.t           = t;
  d             = filter( 'update', d, y );

end

Create a time sequence for the x-axis

%--------------------------------------
[t,tL] = TimeLabl((0:(nSim-1))*dT);

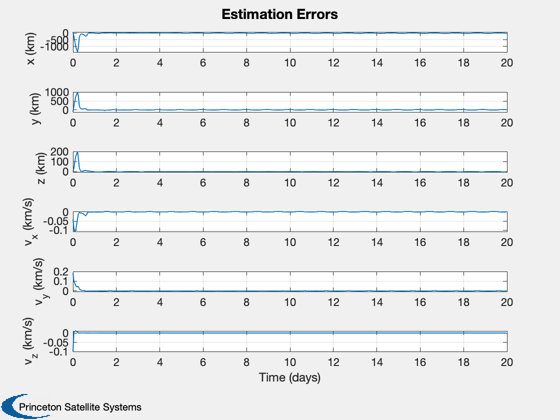
Plot

%-----
err = xP(1:6,:) - xP(7:12,:);
yL  = {'x (km)' 'y (km)' 'z (km)' 'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)'};
Plot2D( t, err, tL, yL, 'Estimation Errors' );

meanError = mean(abs(err(1:3,0.5*nSim:end)),2);

DispWithTitle(meanError,'Mean Error');

%--------------------------------------

Mean Error
       9.0637
       9.1123
      0.47331