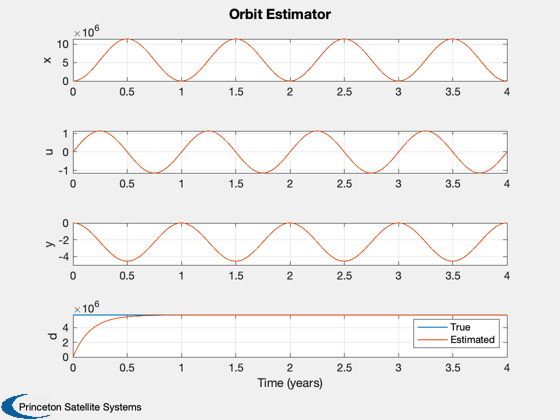
Demonstrates orbit disturbance estimation using linearized equations.

This uses the linearized orbit equations in-plane. A radial disturbance is modeled and estimated. The equations are normalized so that the derivative is respect to wo*t instead of t. This improves the numerical properties of the state transition matrix which otherwise would cause DQCE to fail. DQCE has an inverse in it which is not particularly robust numerically. Generally, this kind of scaling is always a good idea. ------------------------------------------------------------------------- See also C2DZOH, DQCE, Plot2D, TimeLabl, LinOrbNormalized -------------------------------------------------------------------------

The linearized orbit model
Just use the in-plane dynamics
Estimator
These better be in the unit circle
Initial conditions
100-by-100 m^2 solar sail with a mass of 200 kg
Convert plant to discrete time
Convert velocity to km/sec
Generate reasonable time labels

%--------------------------------------------------------------------------
%   Copyright (c) 2002 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

dT           = 10000; % sec
wo           = 2*pi/(86400*365.25); % Earth orbit rate (1 rev/year)
nYears       = 4;
dT           = wo*dT;

The linearized orbit model

%---------------------------
[a, b, c, d] = LinOrbNormalized; % Normalize it

Just use the in-plane dynamics

%-------------------------------
k            = [1 4 5];
a            = a(k,k);
b            = b(k,1);

Estimator

%----------
aE           = a;
aE(:,4)      = [0;1;0];
aE(4,4)      = 0;
bE           = b;
bE(4,1)      = 0;
cE           = eye(3,4);
[aE, bE]     = C2DZOH( aE, bE, dT );  % We don't need bE

kE           = DQCE( aE, eye(size(aE,1)), cE, 10*eye(4), eye(3) );

These better be in the unit circle

%-----------------------------------
eigD         = abs(eig( aE - kE*cE ))

nSim         = floor(nYears*365.25*86400*wo/dT); % 4 years
xPlot        = zeros(8,nSim);

Initial conditions

%-------------------
x            = zeros(3,1);
xE           = [10;0;0;0];

% The disturbance which is solar pressure at 1 au on a

100-by-100 m^2 solar sail with a mass of 200 kg

%-----------------------------------------------------
u            = 1e4*(1358/3e8)*1e-3/(200*wo^2); % km

Convert plant to discrete time

%-------------------------------
[a, b]       = C2DZOH( a, b, dT );

for k = 1:nSim
  xPlot(:,k) = [x;u;xE];
  y          = x;
  x          = a*x + b*u;
  xE         = aE*xE + kE*(y - cE*xE);
end

Convert velocity to km/sec

%---------------------------
xPlot([2 3 6 7],:) = xPlot([2 3 6 7],:)*wo;

Generate reasonable time labels

%--------------------------------
[t,tL] = TimeLabl( (0:(nSim-1))*dT/wo );

Plot2D( t, xPlot, tL, ['x';'u';'y';'d'],'Orbit Estimator','lin',['[1 5]';'[2 6]';'[3 7]';'[4 8]'] );

legend('True','Estimated')


%--------------------------------------
% PSS internal file version information
%--------------------------------------