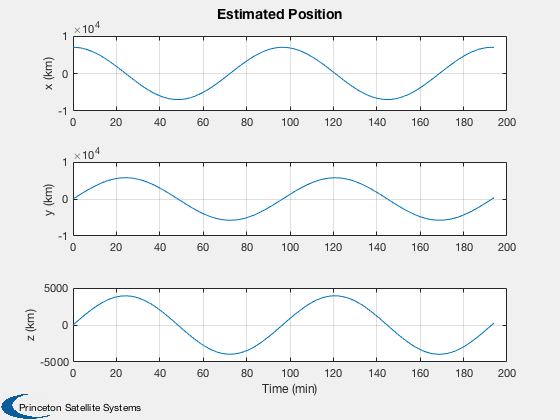
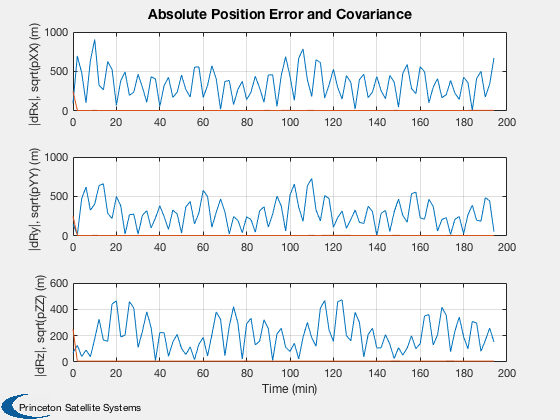
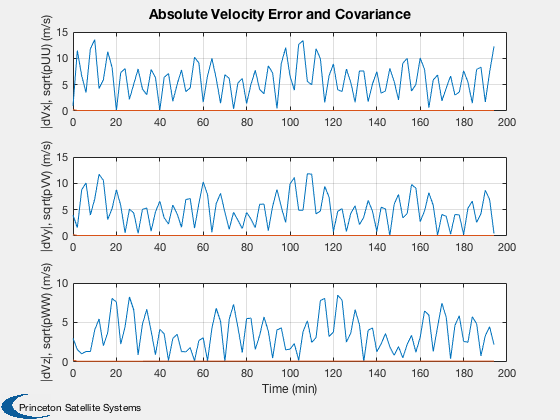
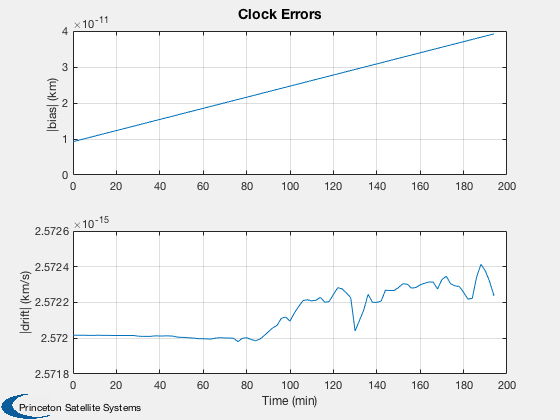
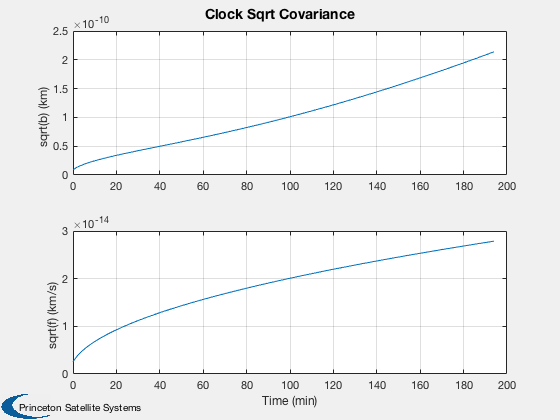
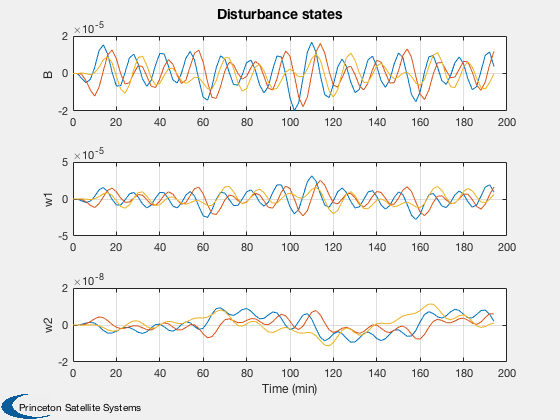
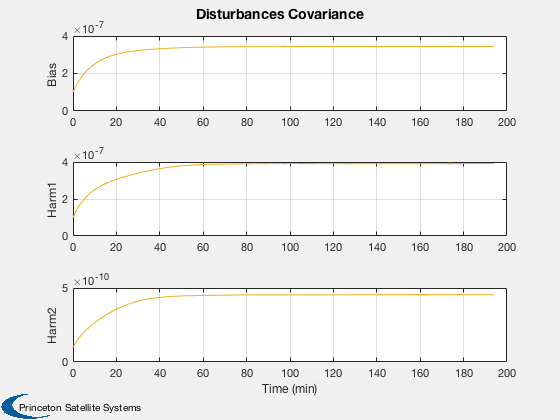
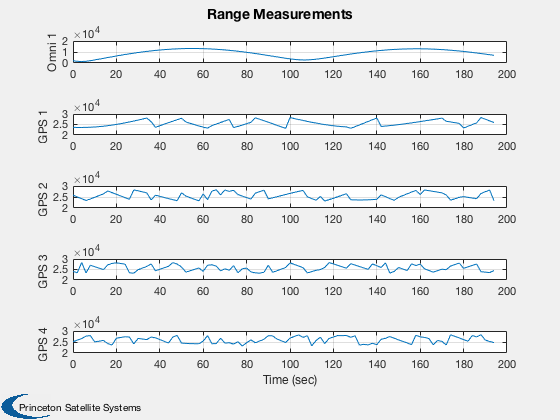
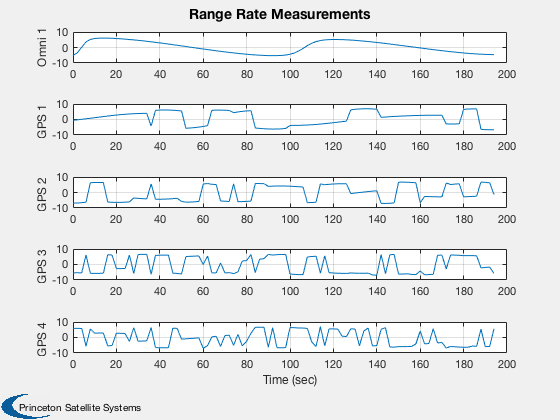
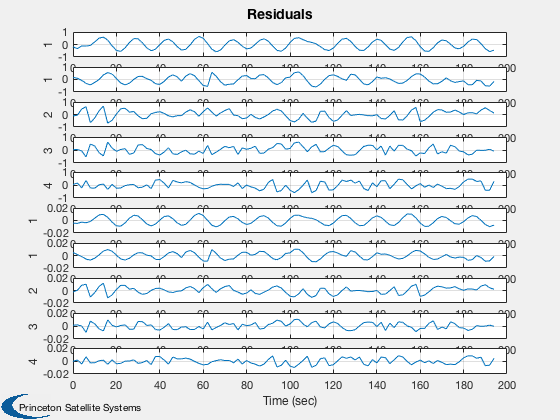
Test the orbit Kalman Filter with omni and GPS measurements.

The simulation and the filter both use the same RHS, FOrbKF, but the simulation uses more terms in the gravity model. ------------------------------------------------------------------------ See also CDKF45, OrbitKFRHS, HRangeMeasurement, RangeMeasurement, GPSReceiver, and FOrbKF, Plot2D, TimeGUI, Cross, RK4, RK45, Date2JD, JD2T, LoadGravityModel, OrbRate, El2RV, Period, EarthRot, EarthRte, GPSSatellite, Omni ------------------------------------------------------------------------

Global for the time GUI
Set up the orbit
Initial estimates
Initialize the sim
For print outs
Set up omni measurements
Set up GPS
Initialize the estimator
Plotting arrays
Numerical integration
Initialize the time display

%-------------------------------------------------------------------------------
%   Copyright (c) 2001-2003 Princeton Satellite Systems, Inc. All rights reserved.
%-------------------------------------------------------------------------------

Global for the time GUI

%------------------------
global simulationAction
simulationAction = ' ';

printIt = 0;

Set up the orbit

%-----------------
el        = [7000 0.6 0 0 0.0001 0];
p         = Period( el(1) );
[r, v]    = El2RV( el );

Initial estimates

%------------------
dT        = 120;
jD        = Date2JD([2001 3 20 13 15 1]);

Initialize the sim

%-------------------
nOrbits   = 2;
nSim      = ceil(nOrbits*p/dT);
bias      = 0.01/3e5/3600; % 0.01 sec/hr one sigma
biasDrift = bias/3600;
x         = [r;v;bias;biasDrift];
t         = 0;
useOmni   = 1;
useGPS    = 1;
gravityModel = LoadGravityModel( 'load file', 'GEMT1.geo' );
simData   = struct('jD',jD,...
                   'gravityModel',gravityModel,...
                   'highFidelity',1,...
                   'nTess',6,...
                   'nZonal',6,...
                   'planetaryOn',1,...
                   'aExt',[0;0;0]);

For print outs

%---------------
if( bias > 0 )
  prefix = 'Clock';
else
  prefix = '';
end

Set up omni measurements

%---------------------------------------------------
rStationEF      = {};
vStationEF      = {};
rStationEF{1}   = [6378.165;0;0];
vStationEF{1}   = Cross( [0;0;EarthRte(jD)], rStationEF{1} );
nOmni           = length(rStationEF);
rOmni           = [0.001 0;0 1e-6].^2;
omni                 = struct();
omni.power           = 5;
omni.range1Sigma     = 0.001;
omni.rangeRate1Sigma = 1e-6;
omni.minimumAngle    = 3*pi/180;

Set up GPS

%-------------------------------------------------------
nGPS                        = 4;
useReceiver                 = 1;
gPSReceiver                 = struct();
gPSReceiver.tSamp           = 1;
gPSReceiver.minimumAltitude = 100;
gPSReceiver.power           = 5;
gPSReceiver.range1Sigma     = 0.001; % noise in model
gPSReceiver.rangeRate1Sigma = 1e-6;
rGPS                        = [0.001 0;0 1e-6].^2;
GPSReceiver( 'initialize', gPSReceiver    );
nMeas = useOmni*nOmni+useGPS*nGPS;

Initialize the estimator

%-------------------------
dR              = 0.25;
dV              = dR/1000;
d               = struct;
d.p             = diag([dR*[1 1 1] dV*[1 1 1] bias biasDrift].^2 );
mu              = 3.98600436e5;
rE              = r + [0.1;-0.15;0.07];
vE              = v + [0.001;-0.004;0.003];
d.x             = [rE;vE;0;0];
d.propagator    = 'RK45';
d.q             = diag([0 0 0 (0.001*mu/7000^2)*[1 1 1] 0.1*bias 0.1*biasDrift].^2);
d.fName         = @OrbitKFRHS;
d.fData         = struct('dFName',@FOrbKF,...
                          'nStates',17,...
                          'jD',jD,...
                          'highFidelity',1,...
                          'gravityModel',gravityModel,...
                          'nTess',2,...
                          'nZonal',2,...
                          'planetaryOn',1,...
                          'aExt',[0;0;0]);
d.hName         = @HRangeMeasurement;
if (d.fData.nStates == 17)
  d.x     = [d.x;zeros(9,1)];
  pDist   = 1e-7*[1 1 1e-3];
  d.p     = diag ([dR*[1 1 1] dV*[1 1 1] bias biasDrift pDist pDist pDist].^2 );
  d.q     = diag([0 0 0 (0.001*mu/7000^2)*[1 1 1] 0.1*bias 0.1*biasDrift 0.1*[pDist pDist pDist]].^2);
end
d.xMeas         = d.x;
d.pMeas         = d.p;
d.hLast         = 0.1*dT;
d.nIterations   = 2;
d.tol           = 1e-6;
range           = [];
rangeRate       = [];
d.r             = {};
j               = 0;

Plotting arrays

%----------------
xPlot   = zeros(length(x),nSim);
xEPlot  = zeros(length(d.x),nSim);
pPlot   = zeros(length(d.x),nSim);
rPlot   = zeros(nMeas*2,nSim);
resPlot = zeros(nMeas*2,nSim);

Numerical integration

%----------------------
tol    = 1e-6;
hLastT = 0.1*dT;
hLastE = 0.1*dT;

Initialize the time display

%----------------------------
[ ratioRealTime, tToGoMem ] =  TimeGUI( nSim, 0, [], 0, dT, 'Orbit Kalman Filter' );

for k = 1:nSim

  % Display the status message
  %---------------------------
  [ ratioRealTime, tToGoMem ] = TimeGUI( nSim, k, tToGoMem, ratioRealTime, dT );

  % Measurement from earth stations
  %--------------------------------
  if useOmni
    mEarth = EarthRot( JD2T( jD ) )';
    for i = 1:nOmni
      j = j + 1;
      % Skip omni model and idealize ground stations as always available
      [range(j,1), rangeRate(j,1)] = RangeMeasurement(  x(1:3,:),  x(4:6,:), x(7:8,:)*3e5, mEarth*rStationEF{i}, mEarth*vStationEF{i} );
      range(j,1)               = range(j,1) + omni.range1Sigma*randn;
      rangeRate(j,1)           = rangeRate(j,1) + omni.rangeRate1Sigma*randn;
      d.r{j}                   = rOmni;
      d.hData(j).rSource       = rStationEF{i};
      d.hData(j).vSource       = vStationEF{i};
  	  d.hData(j).rSourceECI    = mEarth*rStationEF{i};
  	  d.hData(j).vSourceECI    = mEarth*vStationEF{i};
    end
  end % useOmni

  if useGPS
    % Measurements from GPS
    %----------------------
    if( useReceiver )
        % Use GPSReceiver model
        %-------------------------------------
      	GPSReceiver( 'update', struct( 'r',x(1:3),'v', x(4:6), 'jD', jD, 'clockError', x(7:8) )  );
        gPSData = GPSReceiver( 'get output' );
        if gPSData.nSatellites < nGPS
          nGPS = gPSData.nSatellites;
        end
        for i = 1:nGPS
          j = j + 1;
          range(j,1)            = gPSData.range(i);
          rangeRate(j,1)        = gPSData.rangeRate(i);
          d.hData(j).rSourceECI = gPSData.rGPS(:,i);
          d.hData(j).vSourceECI = gPSData.vGPS(:,i);
          d.r{j}                = rGPS;
        end
    else
        % Skip GPS model and idealize GPS satellites as always visible
        [r, v] = GPSSatellite( jD, 'eci' );
        for i = 1:nGPS
          j = j + 1;

          [range(j,1), rangeRate(j,1)] = RangeMeasurement(  x(1:3),  x(4:6), x(7:8), r(:,i), v(:,i) );
          range(j,1)               = range(j,1) + gps.range1Sigma*randn;
          rangeRate(j,1)           = rangeRate(j,1) + gps.rangeRate1Sigma*randn;
          d.hData(j).rSourceECI = r(:,i);
          d.hData(j).vSourceECI = v(:,i);
          d.r{j}                = rGPS;
        end
    end  % useReceiver
  end  % useGPS

  % External disturbance
  %---------------------
  simData.aExt = 1e-7*[0;0;5] + 1e-6*[1;1;1]*sin(OrbRate(el(1))*t);

  % Update the plot array
  %----------------------
  xPlot(:,k)         = x;
  pPlot(:,k)         = diag(d.p);
  xEPlot(:,k)        = d.x;

  % Kalman Filter
  %--------------
  d.secFromStart     = t;
  d.time             = jD;
  d.meas.z           = [range;rangeRate];
  d.dT               = dT;
  d                  = CDKF45( d );

  % Update the plot array
  %----------------------
  rPlot(:,k)         = [range;rangeRate];
  resPlot(:,k)       = d.residual;

  % Propagate
  %----------
  switch d.propagator
    case 'RK45'
      [x,  hLastT] = RK45( @FOrbKF, x,  hLastT, dT, 0, tol, t, simData );
    case 'RK4'
      x      = RK4( @FOrbKF, x, dT, t, simData );
  end
  t                  = t + dT;
  jD                 = jD + dT/86400;
  range     = [];
  rangeRate = [];
  d.r       = {};
  d.hData   = [];
  d.meas.z  = [];
  j         = 0;

  % Time control
  %-------------
  switch simulationAction
    case 'pause'
      pause
      simulationAction = ' ';
    case 'stop'
      return;
    case 'plot'
      break;
  end

end

t  = ( 0:(nSim-1))*dT/60;
dX = 1000*abs(xPlot(1:3,:) - xEPlot(1:3,:));
dV = 1000*abs(xPlot(4:6,:) - xEPlot(4:6,:));
P  = sqrt(pPlot);
yCL = char({'|dRx|, sqrt(pXX) (m)','|dRy|, sqrt(pYY) (m)','|dRz|, sqrt(pZZ) (m)',...
             '|dVx|, sqrt(pUU) (m/s)','|dVy|, sqrt(pVV) (m/s)','|dVz|, sqrt(pWW) (m/s)',...
             ' sqrt(b) (km)','sqrt(f) (km/s)'});

Plot2D( t, xEPlot(1:3,:), 'Time (min)', ['x (km)';'y (km)';'z (km)'],   'Estimated Position' );
Plot2D( t, [dX; 1000*P(1:3,:)], 'Time (min)', yCL(1:3,:),...
      'Absolute Position Error and Covariance','lin',['[1 4]';'[2 5]';'[3 6]'] );
Plot2D( t, [dV; 1000*P(4:6,:)], 'Time (min)', yCL(4:6,:),...
      'Absolute Velocity Error and Covariance','lin',['[1 4]';'[2 5]';'[3 6]'] );
Plot2D( t, abs([xPlot(7:8,:) - xEPlot(7:8,:)]), 'Time (min)', [' |bias| (km)  ';'|drift| (km/s)'],'Clock Errors' );
Plot2D( t, P(7:8,:), 'Time (min)', yCL(7:8,:), 'Clock Sqrt Covariance'    );
if size(xEPlot,1) == 17
  Plot2D( t, xEPlot(9:17,:), 'Time (min)', ['B ';'w1';'w2'],'Disturbance states',...
          'lin',['[1 4 7]';'[2 5 8]';'[3 6 9]']);
  Plot2D( t, P(9:17,:), 'Time (min)', ['Bias ';'Harm1';'Harm2'],...
          'Disturbances Covariance','lin',['[1 4 7]';'[2 5 8]';'[3 6 9]']);
end

yL    = {}; nL = {};
for k = 1:useOmni*nOmni
  yL{k} = ['Omni ' num2str(k)];
  nL{k} = num2str(k);
end
for k = (useOmni*nOmni+1):(nMeas)
  yL{k} = ['GPS ' num2str(k-useOmni*nOmni)];
  nL{k} = num2str(k-useOmni*nOmni);
end
Plot2D( t, rPlot(1:nMeas,:), 'Time (sec)', yL,'Range Measurements' );
Plot2D( t, rPlot(nMeas+1:end,:), 'Time (sec)', yL,'Range Rate Measurements' );
Plot2D( t, resPlot, 'Time (sec)', {nL{:} nL{:}},'Residuals' );

TimeGUI('close');


%--------------------------------------