Contents

Demonstrate orbit estimation using UKFPredict and UKFUpdate.

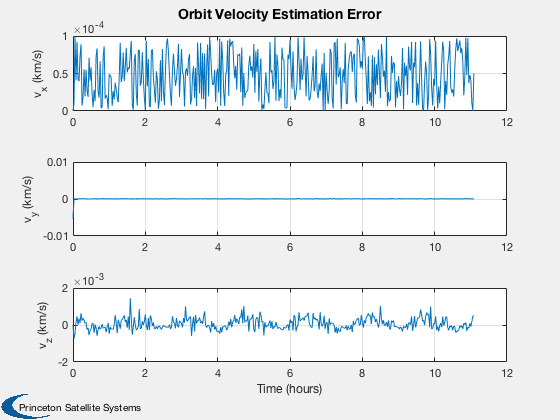
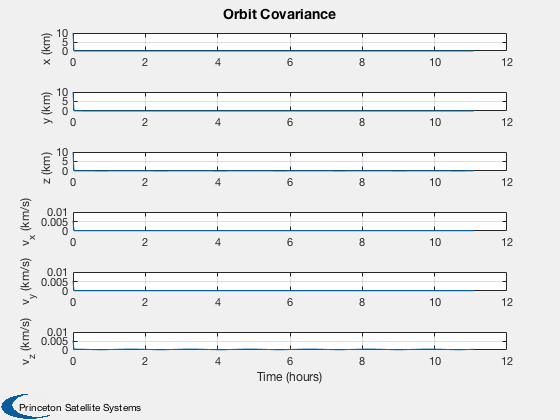
The plots are the covariance, which goes to zero quickly, and the estimation errors.

See also KFInitialize, RK4, UKFPredict, UKFUpdate, RHSOrbitWithDisturbances, UKFWeight, MeasEarthTarget, MeasOrbitState

%--------------------------------------------------------------------------
%   Copyright 2016 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

Simulation parameters

nSim          = 400;
xP            = zeros(19,nSim);
rHSFunData    = RHSOrbit;
r             = 7000;
x             = [r;0;0;0;sqrt(rHSFunData.mu/r);0];
dT            = 100;

% Position and velocity uncertainty
rU            = 10;
vU            = sqrt(rHSFunData.mu/r) - sqrt(rHSFunData.mu/(r+rU));

% State estimate at start
m0            = [r+rU;0;0;0;sqrt(rHSFunData.mu/(r+rU));0];

% Covariance based on the uncertainty
p0            = [rU^2;rU^2;rU^2;vU^2;vU^2;vU^2];
q0            = [0;0;0;1e-3;1e-3;1e-3]; % Plant noise
noise1Sigma 	= 0.1*[1;1;1;1e-3;1e-3;1e-3];
noise1SigmaET = [0.01;0.0001];
r0            = diag(noise1Sigma.^2);
rET0          = diag(noise1SigmaET.^2);

% Initialize the UKF
ukf           = KFInitialize( 'ukf','f',@RHSOrbit,'alpha',1,...
                              'kappa',0,'beta',2,'dT',dT,'fData',rHSFunData,...
                              'p',diag(p0),'q',diag(q0),'x',x,...
                              'm',m0);
ukf           = UKFWeight( ukf );

hData         = struct('noise1Sigma',[0;0;0;0;0;0]);
hDataSim      = struct('noise1Sigma',noise1Sigma);

hETData       = MeasEarthTarget;
hETDataSim    = hETData;
hETDataSim.noise1Sigma = noise1SigmaET;

[ukf.y(2).data, rT]= MeasEarthTarget( x, hETDataSim );

Simulate

t = (0:(nSim-1))*dT;
for k = 1:nSim
  % Plotting
  dRho    = Mag(ukf.m(1:3) - rT) - Mag(x(1:3) - rT);
  xP(:,k) = [ukf.m; x; diag(ukf.p); dRho];

	% Kalman Filter Prediction step
	ukf.t = t(k);
	ukf   = UKFPredict( ukf );

  % Update the RHS
  x  = RK4( @RHSOrbit, x, dT, t(k), rHSFunData );

	% GPS sensor
	ukf.y(1).data        = MeasOrbitState( x, hDataSim );
	ukf.y(1).param.hFun  = @MeasOrbitState;
	ukf.y(1).param.hData = hData;
	ukf.y(1).param.r     = r0;

  % Earth sensor
	[ukf.y(2).data, rT]  = MeasEarthTarget( x, hETDataSim );
	ukf.y(2).param.hFun  = @MeasEarthTarget;
	ukf.y(2).param.hData = hETData;
	ukf.y(2).param.r     = rET0;

  % Filter update step
	ukf = UKFUpdate( ukf );
end

Plot

[t,tL] = TimeLabl(t);

yL = {'x (km)' 'y (km)' 'z (km)' 'v_x (km/s)' 'v_y (km/s)' 'v_z (km/s)' '\rho_T (km)' };

dX = xP(1:6,:) - xP(7:12,:);

Plot2D( t, dX(4:6,:),             tL, yL(4:6),      'Orbit Velocity Estimation Error' );
Plot2D( t, sqrt(xP(13:18,:)),   	tL, yL(1:6),      'Orbit Covariance' );
l = 100:length(t);
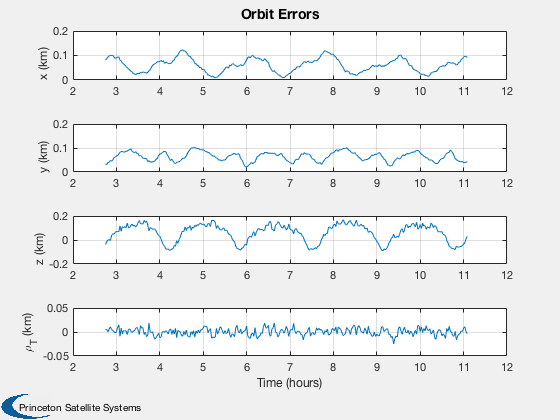
Plot2D( t(l), [dX(1:3,l);xP(19,l)],	tL, yL([1:3 7]),  'Orbit Errors' );


%--------------------------------------

Published with MATLAB® R2016b