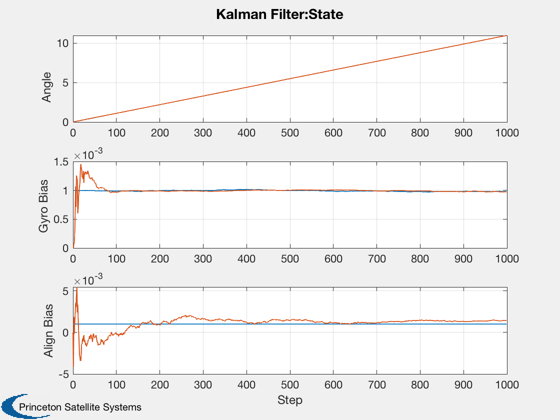
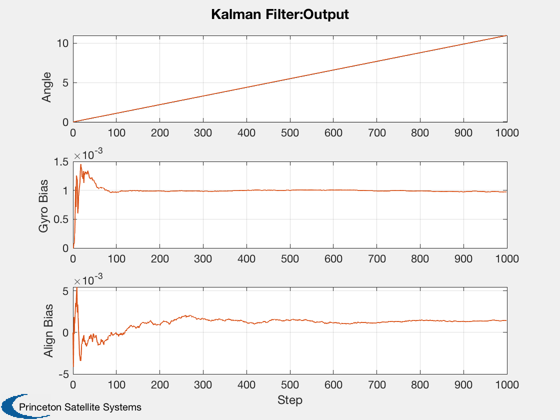
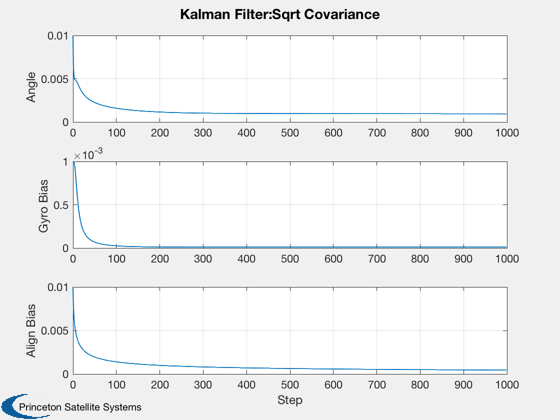
Demonstrate a Kalman Filter for a gyro based attitude determination system.

There are two angle measurements from sensors separated by an initially unknown bias. ------------------------------------------------------------------------- See also C2DZOH, KFilter, Plot2D -------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%   Copyright (c) 2001 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------

State vector [angle;gyro bias;alignment bias]

a = [0 1 0;0 0 0;0 0 0];
b = [1;0;0];
c = [1 0 0;1 0 1];
d = [0;0];

dT = 1;

[a, b] = C2DZOH( a, b, dT );


nSim = 1000;

xPlot = zeros(3,nSim);
ePlot = zeros(3,nSim);
yPlot = zeros(2,nSim);
zPlot = zeros(3,nSim);
pPlot = zeros(3,nSim);

omega = 0.01;

gyroBias1Sigma      = 1e-6;
alignmentBias1Sigma = 1e-7;
measurement1Sigma   = 1e-2;
angle1Sigma         = 1e-5;

x    = [0;omega/10;0.001];
xEst = [0;0;0];
r    = measurement1Sigma^2*eye(2);
q    = diag([angle1Sigma^2,gyroBias1Sigma^2,alignmentBias1Sigma^2]);
p    = diag([.01;.001;.01].^2);
z    = zeros(3,1);

for k = 1:nSim
  y                   = c*x + measurement1Sigma*randn(2,1);
  xPlot(:,k)          = x;
  ePlot(:,k)          = xEst;
  yPlot(:,k)          = y;
  zPlot(:,k)          = z;
  pPlot(:,k)          = sqrt(diag(p));
  [xEst, p, g, z, pY] = KFilter( r, a, q, c, xEst, y, p, [], b*omega );
  x                   = a*x + b*omega + [angle1Sigma;gyroBias1Sigma;alignmentBias1Sigma].*randn(3,1);
end

n = 0:(nSim-1);
yLbl = {'Angle','Gyro Bias','Align Bias'};
Plot2D(n,[xPlot;ePlot],'Step',yLbl,'Kalman Filter:State','lin',['[1 4]';'[2 5]';'[3 6]'])
Plot2D(n,[zPlot;ePlot],'Step',yLbl,'Kalman Filter:Output','lin',['[1 4]';'[2 5]';'[3 6]'])
Plot2D(n,pPlot,'Step',yLbl,'Kalman Filter:Sqrt Covariance')

%--------------------------------------

Published with MATLAB® R2019a