Contents

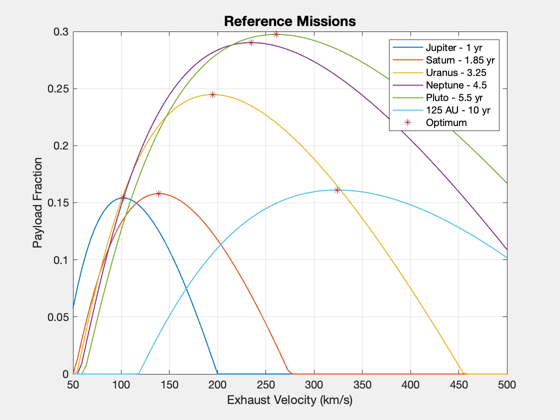
Payload fraction demo for a variety of reference missions

Find the mass-optimal exhaust velocity for a Jupiter mission given other engine parameters.

Our nominal engine has a specific power of 1000 W/kg, a thrust efficiency of 0.4, and a tank structural fraction of 0.05. Our exhaust velocity is in the neighborhood of 100 to 150 km/s. Changing the specific power or efficiency will have a large effect on the payload fraction.

See also: ComputePayloadFraction, OptimalExhaustVelocity, Straight2DStructure

%--------------------------------------------------------------------------
% Copyright 2018, Princeton Satellite Systems, Inc. All rights reserved.
%--------------------------------------------------------------------------

year = 365.25*86400;
au   = Constant('au');
d    = Straight2DStructure;
d.tF = 365.25*86400;      % s
d.dF = 5*au;              % km
d.mP = 1000;              % kg
d.sigma = 750;            % W/kg
d.eta = 0.4;
d.f   = 0.05;
d.uE  = 120;              % km/s

% Reference missions
years = [1 1.85 3.25 4.5 5.5 10];
aUs   = [4 10 20 30 40 125];

uEs = linspace(50,500);  % km/s
lambda = zeros(length(years),100);
for j = 1:length(years)
  d.tF = years(j)*year;
  d.dF = aUs(j)*au;
  for k = 1:100
    d.uE = uEs(k);
    lambda(j,k) = ComputePayloadFraction( d, true );
  end
  [~,kMax] = max(lambda(j,:));
  uEMax(j) = uEs(kMax);
  uEOpts(j) = OptimalExhaustVelocity(d);
  d.uE = uEOpts(j);
  lambdaMax(j) = ComputePayloadFraction( d, true );
end

Plot2D(uEs,lambda,'Exhaust Velocity (km/s)','Payload Fraction','Reference Missions')
hold on
plot(uEOpts,lambdaMax,'*')
legend('Jupiter - 1 yr','Saturn - 1.85 yr','Uranus - 3.25','Neptune - 4.5',...
  'Pluto - 5.5 yr','125 AU - 10 yr','Optimum')

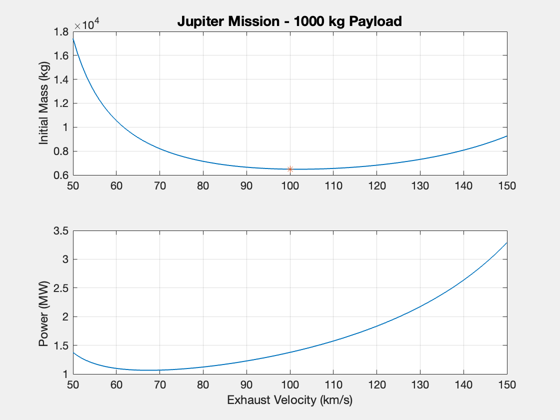
For a 1000 kg payload to Jupiter, calculate over a narrower band of uE

uEOpt = uEMax(1);
uEs2 = linspace(uEOpt-50,uEOpt+50,101);
lambda2 = zeros(size(uEs2));
alpha = zeros(size(uEs2));
d.tF = years(1)*year;
d.dF = aUs(1)*au;
for k = 1:length(uEs2)
  d.uE = uEs2(k);
  [lambda2(k),alpha(k)] = ComputePayloadFraction( d, true );
end

mP = 1000;
m0 = mP./lambda2;
P  = mP./alpha;
% limit values for sake of plot
m0(m0>5e5) = 5e5;
P(P>3e8) = 3e8;
Plot2D(uEs2,[m0;P*1e-6],'Exhaust Velocity (km/s)',{'Initial Mass (kg)','Power (MW)'},...
  'Jupiter Mission - 1000 kg Payload')
subplot(2,1,1)
hold on
plot(uEs2(51),m0(51),'*')

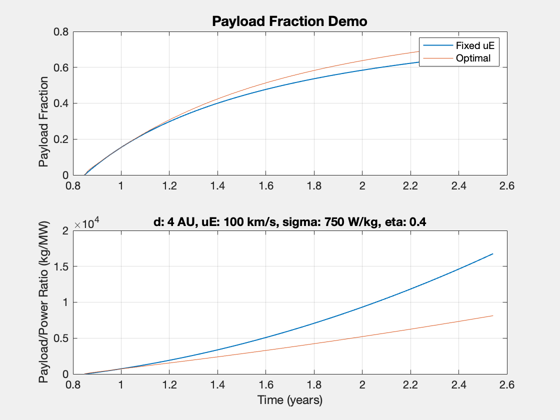
For an array of times, at a fixed uE

d.uE = uEMax(1);
d.dF = aUs(1)*au;
tMin = ZeroPayloadTime( d );
ts   = linspace(1,3);
lambdas = zeros(1,length(ts));
alphas = zeros(1,length(ts));
lambdas2 = zeros(1,length(ts));
alphas2 = zeros(1,length(ts));
for k = 1:length(ts)
  d.tF = ts(k)*tMin;
  d.uE = uEMax(1);
  [lambdas(k),alphas(k)] = ComputePayloadFraction( d, true );
  uEOpt(k) = OptimalExhaustVelocity(d);
  d.uE = uEOpt(k);
  if uEOpt(k)~= 0
    [lambdas2(k),alphas2(k)] = ComputePayloadFraction( d, true );
  end
end
[tPlot,tLabl] = TimeLabl(ts*tMin);
Plot2D(tPlot,[lambdas;alphas*1e6],tLabl,{'Payload Fraction','Payload/Power Ratio (kg/MW)'},...
  'Payload Fraction Demo');
subplot(2,1,1)
hold on
plot(tPlot,lambdas2)
legend('Fixed uE','Optimal')
subplot(2,1,2)
hold on
plot(tPlot,alphas2*1e6)
title(sprintf('d: %g AU, uE: %g km/s, sigma: %g W/kg, eta: %g',...
  d.dF/au,uEMax(1),d.sigma,d.eta))


%--------------------------------------

% $Id: 22001300e3cbed0e54a99f071fcac10f202e6985 $

Warning: Distance not achievable for sigma 

Published with MATLAB® R2024a