Contents

Power-Limited Rocket (SLPL) Demo

This set of functions will find the optimal mission for a straight-line trajectory with a fixed power level, allowing acceleration to vary. (Acceleration becomes infinite at the switch point.)

See also: SLPLDataStructure, SLPLSolver, Plot2D

------------------------------------------------------------------------

%--------------------------------------------------------------------------
%   Copyright (c) 2021 Princeton Satellite Systems, Inc.
%   All rights reserved.
%--------------------------------------------------------------------------
%   Since 2021.1
%--------------------------------------------------------------------------

Fuel-mass limited demo

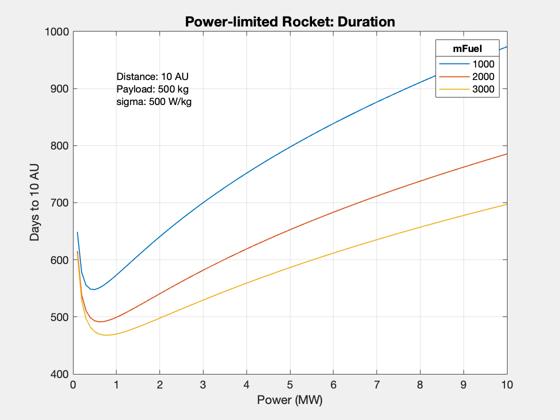
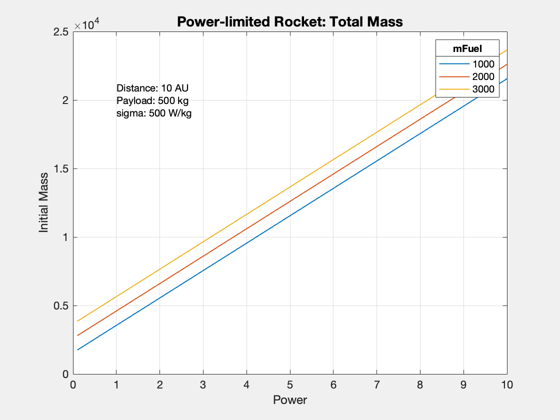
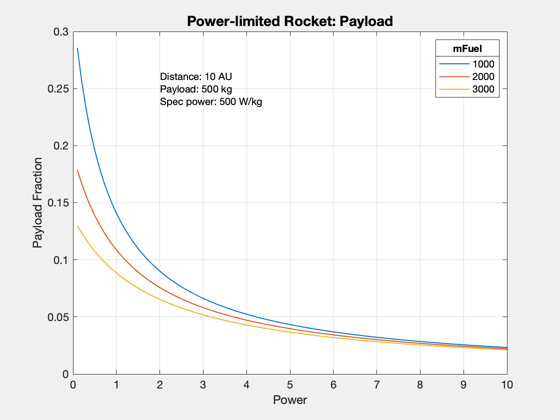
For a fixed fuel mass, solve for the optimal trip time.

AU = Constant('au');
dF = 10*AU;
Pj = linspace(1e5,1e7);

sigma  = 500;  % engine mass scales with jet power, Wj/kg
f      = 0.05; % tank fraction
mP     = 500;  % payload mass, kg
mF     = [1000 2000 3000]; % Fuel mass, kg

% Reserve output array size
tF = zeros(length(mF),length(Pj));
m0 = zeros(length(mF),length(Pj));
lambda = zeros(length(mF),length(Pj));

d = SLPLDataStructure;
d.dF = dF;
d.vF = 0;

for k = 1:length(Pj)
  for j = 1:length(mF)
    mE = Pj(k)/sigma;
    mD = mE+mP+f*mF(j);
    m0(j,k) = mD+mF(j);
    lambda(j,k) = mP/m0(j,k);

    d.Pj = Pj(k);
    d.mD = mD;
    d.m0 = m0(j,k);
    d.tF = [];

    data = SLPLSolver( d );
    tF(j,k) = data.tF;
  end
end

% Plots
Plot2D(Pj*1e-6,tF/86400,'Power (MW)','Days to 10 AU','Power-limited Rocket: Duration')
text(1,900,sprintf('Distance: %g AU\nPayload: %g kg\nsigma: %g W/kg',dF/AU,mP,sigma))
ll = legend(num2str(mF'));
ll.Title.String = 'mFuel';

Plot2D(Pj*1e-6,m0,'Power','Initial Mass','Power-limited Rocket: Total Mass')
text(1,20000,sprintf('Distance: %g AU\nPayload: %g kg\nsigma: %g W/kg',dF/AU,mP,sigma))
ll = legend(num2str(mF'));
ll.Title.String = 'mFuel';

Plot2D(Pj*1e-6,lambda,'Power','Payload Fraction','Power-limited Rocket: Payload')
text(2,0.25,sprintf('Distance: %g AU\nPayload: %g kg\nSpec power: %g W/kg',dF/AU,mP,sigma))
ll = legend(num2str(mF'));
ll.Title.String = 'mFuel';

Initial mass-limited demo

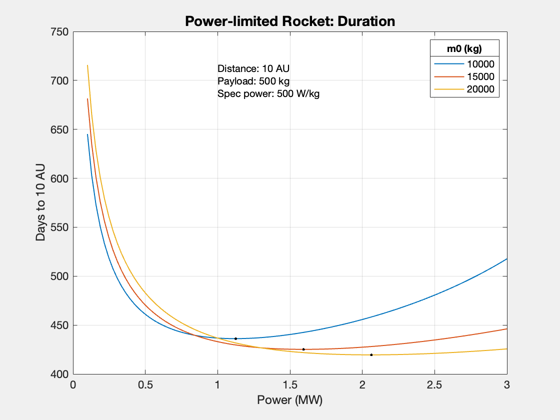
Fix the total initial mass and solve for optimal duration. The payload fraction is constant.

tF = [];
mP = 500;
Pj = linspace(1e5,3e6);
m0 = [10000 15000 20000]; % Initial mass

% Reserve output array size
mF = zeros(length(m0),length(Pj));
tF = zeros(length(m0),length(Pj));
for k = 1:length(Pj)
  for j = 1:length(m0)
    mE = Pj(k)/sigma;
    mL = m0(j) - mE - mP;
    mF(j,k) = mL/(1+f);
    mD = mE + mP + f*mF(j,k);

    d.Pj = Pj(k);
    d.mD = mD;
    d.m0 = m0(j);
    d.tF = [];
    data = SLPLSolver( d );
    tF(j,k) = data.tF;
  end
end

Plot2D(Pj*1e-6,tF/86400,'Power (MW)','Days to 10 AU','Power-limited Rocket: Duration')
text(1,700,sprintf('Distance: %g AU\nPayload: %g kg\nSpec power: %g W/kg',dF/AU,mP,sigma))
[ts,js] = min(tF,[],2);
hold on;
plot(Pj(js)*1e-6,ts/86400,'k.')
ll = legend(num2str(m0'));
ll.Title.String = 'm0 (kg)';


%--------------------------------------

% $Id: 031d511720cba6f068eb2b14e2c4bd09de0a65f2 $

Published with MATLAB® R2024a