Design a linear quadratic temperature controller

Since version 9.
------------------------------------------------------------------------
See also AC, C2DZOH, QCR, Plot2D, TimeLabl
------------------------------------------------------------------------

Contents

%--------------------------------------------------------------------------
%    Copyright (c) 2010 Princeton Satellite Systems, Inc.
%    All Rights Reserved
%--------------------------------------------------------------------------

clear T; clear Q; clear H;

Create a test conductance matrix

dT/dt = aT + bq where q is the input heat flux or loss

%---------------------------------------
n = 10;
a = zeros(n,n);
for k = 1:n
	a(k,k) = -2;
	j = k+1;
	if( j < n+1 )
    a(j,k) = 1;
	end
	j = k-1;
	if( j >  0 )
     a(j,k) = 1;
	end
end

a(1,1)   = -1;
a(n,n)   = -1;

disp('Eigenvalues of a')
eig(a)

b        = eye(n);
r        = eye(n);
q        = eye(n);

dT       = 10;

gain     = QCR( a, b, q, 100000*r );

disp('Eigenvalues of the closed loop system')
eig(a-b*gain)

[aC,gain] = C2DZOH( a, gain, dT );
[a, b]    = C2DZOH( a, b, dT );

eig(a-b*gain)

x        = 300*ones(n,1);
xS       = x;
qC       = zeros(n,1);

nSim     = 2000;
xP       = zeros(3*n,nSim);
t        = 0;

qH       = (rand(n,1) - 0.5);

Eigenvalues of a
ans =
      -3.9021
       -3.618
      -3.1756
       -2.618
           -2
       -1.382
     -0.82443
     -0.38197
    -0.097887
  -1.1143e-17
Eigenvalues of the closed loop system
ans =
      -3.9021
       -3.618
      -3.1756
       -2.618
           -2
       -1.382
     -0.82444
   -0.0031623
    -0.097938
     -0.38198
ans =
      0.68377
      0.37366
     0.021849
   0.00025384
  -8.9856e-07
  -6.2294e-07
  -2.7864e-07
  -1.5614e-07
  -1.0557e-07
  -8.4153e-08

Simulation loop

%----------------
for k = 1:nSim

    % Bidirectional input heat flux
    %------------------------------
    if( k < 100 || (k > 300 && k < 700)  )
        q = qH;
    else
        q = zeros(n,1);
    end

    qC      = -gain*(x - xS);

    j       = find(qC < 0);
    qC(j)   = 0;

    xP(:,k) = [x;q;qC];

    % State update
    %-------------
    x       = a*x + b*(q + qC);
    t       = t + dT;
end

Set the time label

%-------------------
[t, tL] = TimeLabl((0:nSim-1)*dT);

T = cell(1,n);
Q = cell(1,n);
H = cell(1,n);

for k = 1:n
	T{k} = sprintf('T%d',k);
	Q{k} = sprintf('Q%d',k);
	H{k} = sprintf('H%d',k);
end

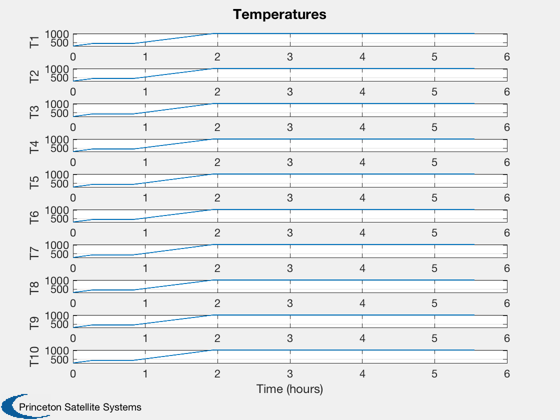
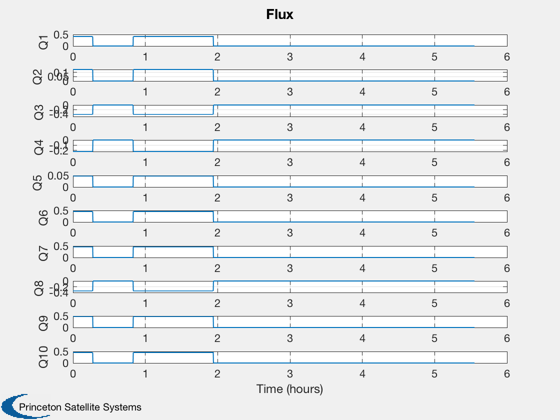
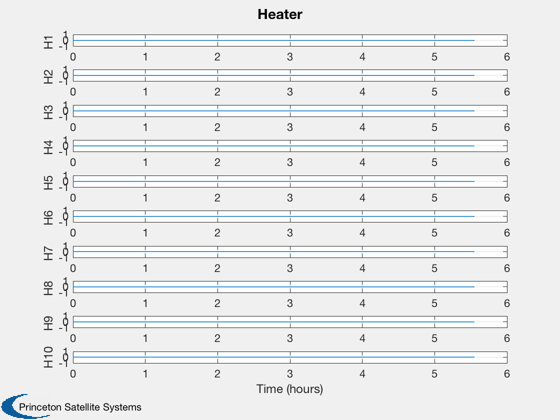
Plotting

%---------
Plot2D( t, xP( 1: n,:), tL, T, 'Temperatures' )
Plot2D( t, xP( n+1:2*n,:), tL, Q, 'Flux'      )
Plot2D( t, xP(2*n+1:3*n,:), tL, H, 'Heater'   )

%--------------------------------------

Published with MATLAB® R2019a